Da Celsius a Fahrenheit e da Kg a Libbre, giocando con i numeri

Come si passa da Celsius a Fahrenheit? E che relazione c’è tra un peso espresso in chilogrammi e lo stesso peso espresso in libbre?
Non sono domande di importanza vitale, ma possono regalare un viaggio piacevole tra storia e matematica.

---

Da Celsius a Fahrenheit, da dove arrivano le due scale di misura

Il fisico tedesco Daniel Gabriel Fahrenheit propose la sua definizione di scala per la misura della temperatura nel 1724. Utilizzò due punti di riferimento:

• la temperatura a cui fonde una miscela di ghiaccio e sale ammoniaco, definita come 0°F;
• la temperatura corporea di un uomo sano, che avrebbe dovuto misurare 100°F.

Sul secondo punto di riferimento avrebbe potuto far meglio, e infatti in seguito la scala fu ricalibrata, senza stravolgere le misure,  per avere 180°F tra due nuovi punti di riferimento:

• la temperatura di congelamento dell’acqua, arrotondata a 32°F;
• quella di ebollizione dell’acqua, arrotondata a 212°F.

Con questa nuova definizione, 100°F denota già un leggero stato febbrile, ma l’abitudine che si era ormai radicata nelle persone non ne usciva stravolta.

Qualche anno dopo, nel 1742, arriva la scala Celsius, proposta dall’astronomo svedese Anders Celsius. Partendo from scratch, nella sua definizione ha un approccio più razionale: il punto in cui l’acqua diventa ghiaccio è di 0°C, mentre il punto in cui l’acqua bolle è a 100 °C. L’intervallo tra i due fenomeni misura perciò 100°C.

Si ha quindi la relazione: 180°F = 100°C, che semplificata dà: 9°F = 5°C.

Per passare, ad esempio, da Celsius a Fahrenheit, la formula corretta è: F = 5 ⁄ 9 C + 32.

La misura in gradi Celsius si è diffusa rapidamente in quasi tutto il mondo, con l’esclusione di alcuni paesi anglofoni, dove la temperatura è ancora misurata pervicacemente con il Sistema imperiale britannico.

Quando capita di dover passare da Celsius a Fahrenheit

Nella vita di tutti i giorni non succede di doversi arrovellare tra Sistema imperiale britannico e Sistema internazionale di unità di misura. Ma, se capita di viaggiare, ad esempio, negli Stati Uniti, allora una regoletta mnemonica torna utile, almeno per ascoltare in modo consapevole le notizie meteo.

Quando è capitato a me, svariato tempo fa, i miei colleghi residenti negli US mi passarono la regola: 61°F ≈ 16°C. Da lì in avanti ogni 9°F varia di 5°C.
Quindi, se a San Francisco il meteo mi dice che ci sono 75°F, allora, mentalmente devo calcolare:

75 – 61 = 14, 14 = 9 + 5, quindi la variazione in °C è di circa 5 + 3 = 8 gradi e, infine, in Celsius dovrebbero essere 16 + 8 = 24°C.

In realtà sarebbero 23,9°C, però devo confessare che l’esempio l’ho scelto ad hoc, con altri valori di temperatura lo scostamento potrebbe essere più ampio. Ad ogni modo, per le normali esigenze, questa piccola ginnastica mentale aiuta.

Qualche giorno fa mi sono invece imbattuto su Instagram nella regola riportata qui a lato.
Utilizzando questo algoritmo, i 95°F di San Francisco diverrebbero:

75 – 30 = 45, 45/2 = 22,5 °C.

L’approssimazione va ancora abbastanza bene, e i calcoli sono decisamente meno complicati.

Un foglio excel aiuta a stimare l’errore delle due approssimazioni, almeno per il campo tra 32°F e 100°F, equivalente all’intervallo tra 0°C e 37,8°C.

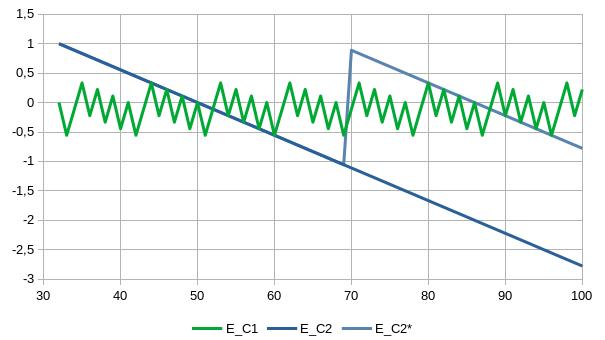
In verde c’è l’errore di approssimazione del primo metodo, quello che mi arrivò dall’ambito ingegneri/informatici. È decisamente più preciso, a patto di effettuare mentalmente in modo corretto l’approssimazione al grado dei 5 ⁄ 9 della differenza di temperatura.

Il secondo metodo, quello che mi arriva da Instagram, è visualizzato in blu, e comincia a sballare di oltre 2°C dagli 86°F (30°C) in avanti.
Si potrebbe migliorare l’approssimazione con una semplice modifica: sottrarre 2°C per temperature di 70°F e oltre. Nel grafico il risultato è rappresentato dalla linea azzurra. In questo modo l’errore di approssimazione si mantiene comunque minore di 1°C e la regola non si complica poi di tanto.

Un po’ di storia della libbra

Un problema simile a quello appena visto della conversione da Celsius a Fahrenheit si pone per il passagio da libbre a chilogrammi.
La libbra, unità di massa del sistema britannico, corrisponde (ci informa Wikipedia) a 0,45359237 kg. E ci fermiamo al 7 perché va già bene così, ma si potrebbe proseguire.
Deriva il suo nome dal latino libra, cioè bilancia. Un’unità di peso condivisa è alla base anche degli scambi di oro, e da qui deriva anche il nome lira di diverse valute in giro per il mondo, compresa l’Italia fino a un quarto di secolo fa circa.

La libbra latina equivaleva però a 0,327168 kg, in linea (sembrerebbe) con un po’ di unità utilizzate in Italia nel Medioevo. Esempi: 0,32075899 a Napoli, 0,34513 a Ferrara, 0,33954 in Toscana.
La libbra inglese sempre più vicina a un’altra unità di massa romana, la mina, equivalente a 0,436224 Kg.

Per completare il quadro, gli Stati Uniti hanno una loro libbra, praticamente uguale a quella britannica, da cui si discosta per meno di una parte su 10 milioni (Wikipedia).

Insomma, viva la Rivoluzione francese che spianò la strada al Sistema Internazionale di Unità di Misura.

Da libbre a chilogrammi

La relazione matematica tra libbra (britannica) e chilogrammi è riportata poco più su: 1 Lb = 0,45359237 kg.
Impensabile utilizzare questa formula per conversioni al volo al supermercato. Tornerebbe utile un’approssimazione frazionaria, cioè una frazione A / B il cui valore sia abbastanza vicino a 0,45359237 e con valori di A e B facilmente memorizzabili.

Vari algoritmi sono applicabili per trovare frazioni che approssimano in modo via via più preciso un valore dato.
Esploriamone un paio: approssimazione per incrementi unitari (via excel) e con frazioni continue (via codice Python).

Approssimazione per incrementi unitari

L’idea dietro questo elementare algoritmo è molto semplice:

• si utilizza come punto di partenza la frazione N / D = 1 / 1;
• se il valore della frazione è minore dell’obiettivo da raggiungere, incremento di 1 il numeratore N, se è maggiore allora incremento il denominatore;
• l’algoritmo si arresta quando la frazione ha raggiunto esattamente il valore cercato, oppure si è raggiunta la precisione voluta.

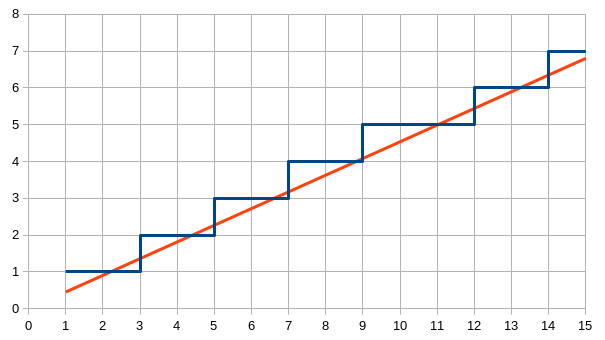
L’immagine chiarisce l’idea:

A occhio si direbbe che 4/9 e poi 5/11 siano buone approssimazione (5/11 = 0,454545…). Un file excel può fare meglio della vista.

Mano all’Excel (o meglio LibreOffice Calc)

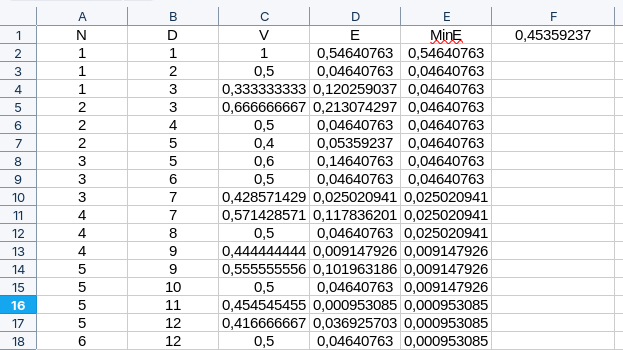
In un foglio di calcolo riportiamo nelle colonne A, B, C D ed E i valori rispettivamente di numeratore, denominatore, valore della frazione, errore, errore minimo fino a quel punto. Nella cella F1 si inserisce il valore di obiettivo 0,45359237.

Le formule da inserire:

• nella cella A1 scrivo l’intestazione per indicare il numeratore, N;
• nella cella A2 inserisco il valore di partenza 1;
• nella cella A3 invece la formula: =SE(A2/B2<$F$1;A2+1;A2), da copiare in basso. La logica è abbastanza semplice: se il rapporto tra numeratore e denominatore della riga precedente è minore del valore di obiettivo (F1), allore incremento il numeratore, altrimenti lo lascio inalterato;
• nelle celle B1, B2 e B3 vanno valori equivalenti, in particolare la formula diventa: =SE(A2/B2>$F$1;B2+1;B2), cioè incrementando il denominatore quando la frazione è oltre l’obiettivo;
• nella colonna C riporto il valore della frazione;
• nella colonna D l’errore, come scostamento in valore assoluto dall’obiettivo, cioè in E3: =ASS($F$1-C3);
• nella colonna E memorizzo il minimo dell’errore, ponendo in E2 l’errore iniziale e in E3 la formula =SE(D3<E2;D3;E2).

Basta copiare verso il basso le formule, fino a quando l’errore scende sotto una soglia voluta. Notare che, nel caso si arrivi a un N/D esattamente uguale al valore di obiettivo, dal passo successivo non cambieranno né N né D.

La frazione 5/11 si conferma la miglior approssimazione, con un errore minore di un millesimo, fino a quando viene spodestata, anche se di poco, da 24/53. Molto più giù, dopo alcuni record temporanei, si trova 39/86 con una precisione di circa una parte su diecimila.

Approssimazione mediante frazioni continue

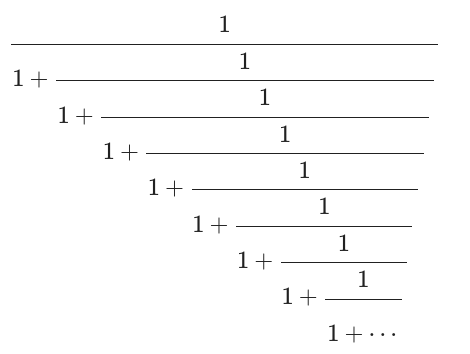
Immaginate di avere un’espressione come questa:

Questa simpatica iper-frazione si chiama frazione continua, e può essere infinita, come in questo caso, oppure finita, fermandosi dopo un certo numero di piani. Il modo formale per definire una frazione di questo tipo è quello di racchiudere la sequenza di valori tra parentesi quadre. In questo caso si ha: [0;1,1,1,1, …], dove il primo 0 indica che non c’è un addendo iniziale.

Le frazioni continue hanno le basi storiche nel 1613, quando il matematico Pietro Cataldi ne fornì la prima definizione formale, e hanno importanti proprietà. Ma come si calcola il valore di questa espressione?
In questo caso molto semplice, basta considerare che, se poniamo a x il suo valore, il suo reciproco 1 / x sarà uguale a 1 + x. Per sincerarsene, basta coprire con un dito il numeratore al top e vedere cosa rimane.

L’equazione 1/x = 1 + x è una semplice equazione di secondo grado: x² + x – 1 = 0, la cui soluzione positiva è pari a (radq(5) – 1 )/2. Risultato notevole, basta aggiungere 1 per ottenere il rapporto aureo.

In generale è dimostrato che, data l’espansione di un numero irrazionale in frazione continua, se ci si ferma a un dato numero di piani, la frazione semplificata N/D che si ottiene è la miglior approssimazione al numero dato, con un denominatore non maggiore di D.

L’applicazione dell’algoritmo a libbra e chilogrammo

La frazione continua, dato un valore di obiettivo, si calcola con un algoritmo ispirato al metodo di Euclide per il calcolo del massimo comun divisore di due numeri.
Il codice Python che segue si appoggia due funzioni, la prima per calcolare un dato numero di termini dello sviluppo in frazione continua, il secondo per calcolare l’equivalente frazione semplificata.

from fractions import Fraction

from fractions import Fraction

def frazione_continua_approssimata(costante, termini):
    intero = int(costante)
    resto = costante - intero
    approssimazione = [intero]
    for _ in range(termini - 1):
        if resto:
            nuovo_numero = 1 / resto
            intero_nuovo = int(nuovo_numero)
            approssimazione.append(intero_nuovo)
            resto = nuovo_numero - intero_nuovo
        else:
            break
        print (approssimazione, "-->",frazione_continua(approssimazione))
    return approssimazione

def frazione_continua(approximation):
    terms = len(approximation)
    if terms == 0:
        return 0
    if terms == 1:
        return approximation[0]
    return approximation[0] + Fraction(1, frazione_continua(approximation[1:]))

# costante = 3.14159265358
costante = 0.45359237
termini = 8
approssimazione = frazione_continua_approssimata(costante, termini)

L’output del codice, eseguito su Google Colab, è questo:

[0, 2] --> 1/2
[0, 2, 4] --> 4/9
[0, 2, 4, 1] --> 5/11
[0, 2, 4, 1, 7] --> 39/86
[0, 2, 4, 1, 7, 1] --> 44/97
[0, 2, 4, 1, 7, 1, 5] --> 259/571
[0, 2, 4, 1, 7, 1, 5, 1] --> 303/668

Il codice conferma 4/9 e 5/11 come prime migliori approssimazioni, per poi saltare direttamente a 39/86.

---

Indagare su come convertire da Celsius a Fahrenheit e da libbre a chilogrammi non porta evidentemente a grandi scoperte. Ma questo tipo di gioco mi intriga non poco: una miscela di ricordi scolastici e letture giovanili, un po’ di ginnastica informatica e matematica letta qui e là nel tempo. Oltre che divertire dovrebbe anche prevenire la perdita di memoria e  l’invecchiamento mentale, pare. Però non ricordo dove l’ho letto.

Immagine di Alexandru Strujac da Pixabay.