Nel 1976 il biologo Robert May pubblicava un’interessante analisi su un modello di sistema dinamico applicabile in vari campi di studi, dalla biologia alle scienze sociali. Questo modello, noto come logistic map, può essere utilizzato, ad esempio, per descrivere matematicamente l’andamento della popolazione di un particolare ambiente, sotto particolari condizioni.
Si supponga che quel particolare ambiente possa ospitare al massimo una determinata popolazione di individui e che, in un certo istante t, la popolazione sia una frazione xt del massimo possibile. Al passo generazionale successivo, la popolazione sarà cambiata, in proporzione a:
- popolazione presente (xt);
- disponibilità di spazio per la crescita (1 – xt);
- rapidità di crescita (r).
Quindi, in formula:
xt+1 = r × xt × (1 – xt)
Robert May mostrò che la logistic map può descrivere comportamenti che vanno dall’ordine più piatto immaginabile fino al completo caos, in base al punto di partenza assegnato alla popolazione e, soprattutto, al valore assegnato alla rapidità di crescita r.
La logistic map, nella sua semplicità, non è utilizzabile per rappresentare l’andamento della popolazione sulla Terra, per diversi motivi. La capacità del nostro pianeta non è rimasta costante nei millenni, ad esempio, ma si è estesa nel tempo grazie ai progressi tecnologici e organizzativi. Eppure questo semplice modello mostra i pericoli insiti in un tasso di crescita elevato, che non abbia ben presente la sostenibilità.
Ripercorriamo l’analisi di May, con l’aiuto di un foglio di calcolo (Libre Office Calc o Excel).
Campo di variabilità della rapidità di crescita
Quali valori ha senso esplorare per r, la rapidità di crescita?
La prima ovvia osservazione è che r deve essere positivo, se si vuole che la popolazione presente sia espressa da una percentuale x positiva.
Un po’ meno ovvio è che, per la stessa ragione, r deve essere minore di 4. A questa conclusione si arriva osservando che il valore massimo raggiunto da:
x (1 – x)
si ottiene quando x = 0.5, ed è pari a 0.5 × 0.5 = 0.25. Con un valore di r maggiore di 4, x supererebbe il 100% della popolazione consentita e, al passo successivo, diverrebbe negativo.
La decrescita, nemmeno tanto felice
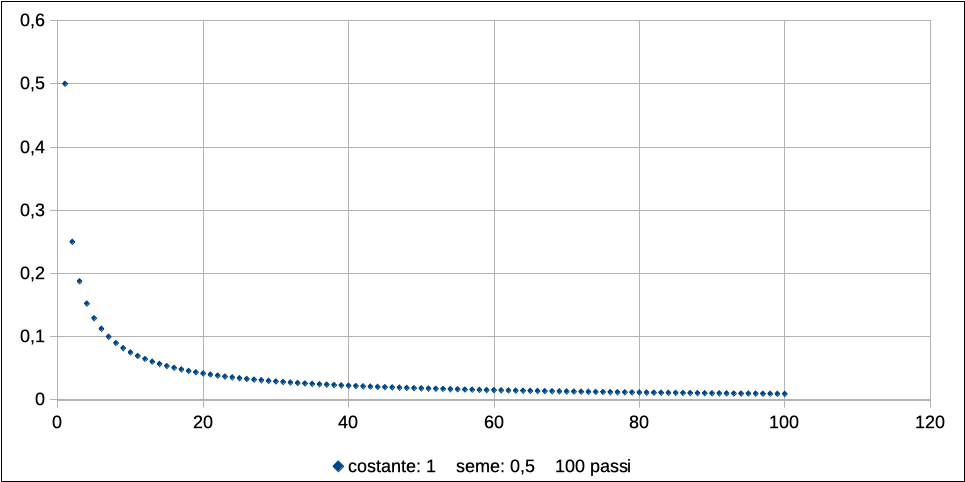
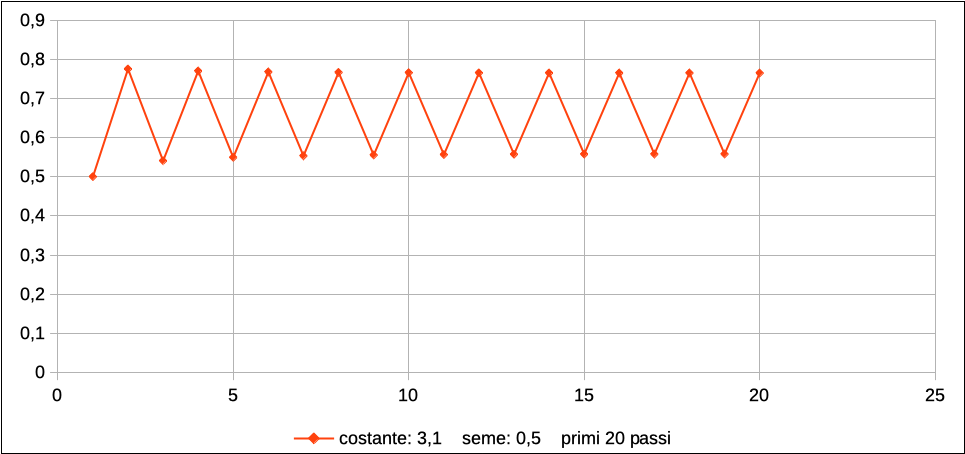
Per valori di r che vanno da 0 a 1, la popolazione non può che decrescere, poiché xt+1 sarà sempre minore di xt. Quindi, di generazione in generazione, la presenza di popolazione x diminuirà progressivamente, tendendo a 0.
La figura che segue descrive l’andamento con r = 1, partendo da una popolazione iniziale di 0.5 (50% del massimo possibile).
Logistic map: la crescita stabile e sostenibile
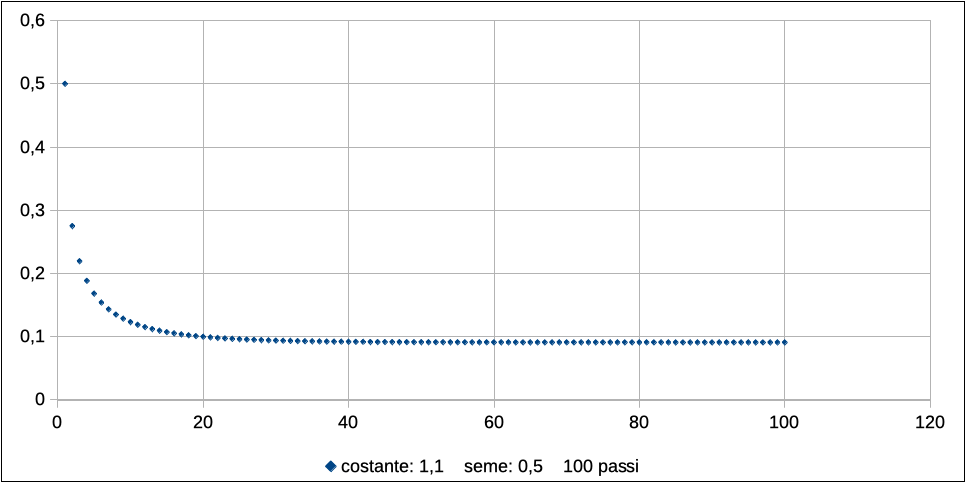
Basta però un valore di r appena superiore a 1, perché la popolazione raggiunga un livello stabile e duraturo.
Il valore di stabilità per la popolazione si ottiene risolvendo la semplice equazione:
x = r x (1-x)
semplificando: 1/r = 1 – x
quindi: x = 1 – 1/r
Nel caso della figura, r = 1.1 e quindi x = 1 – 1/1.1 = 0, 090909…
Un caso più complicato di stabilità
L’equilibrio appena descritto non è il solo possibile. Si può provare a capire se esiste, ad esempio, un equilibrio in cui la popolazione oscilla, di generazione in generazione, tra due determinati valori.
Un equilibrio di questo genere è descritto dalle equazioni:
y = r x (1-x)
x = r y (1-y)
Risolvendo in x si ottiene l’equazione di terzo grado:
r3 x3 – 2 r3 x2 + r2(r+1)x – (r2 – 1) = 0
Qui occorre rispolverare la divisione tra polinomi (credo prima liceo), per scoprire che x = 1 – 1/r è una soluzione anche di questa equazione, e che l’equazione:
r3 x2 – r2(r+1)x + r(r + 1) = 0
ha le altre due soluzioni, che saranno reali solo quando il delta dell’equazione è maggiore zero (e qui bisogna ritornare in seconda liceo).
La condizione di oscillazione tra due punti stabili si ottiene quindi quando:
r > 3
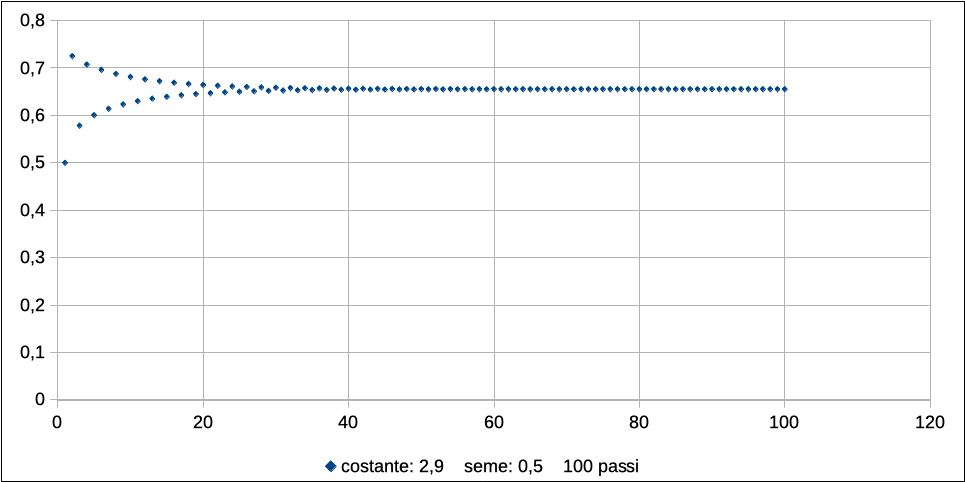
Ecco come si comporta il sistema per r = 2,9, sempre partendo da una popolazione pari al 50% del massimo consentito:
La traiettoria di crescita della popolazione si avvicina progressivamente al valore di stabilità di 1 – 1/2.9 = 0,65517…
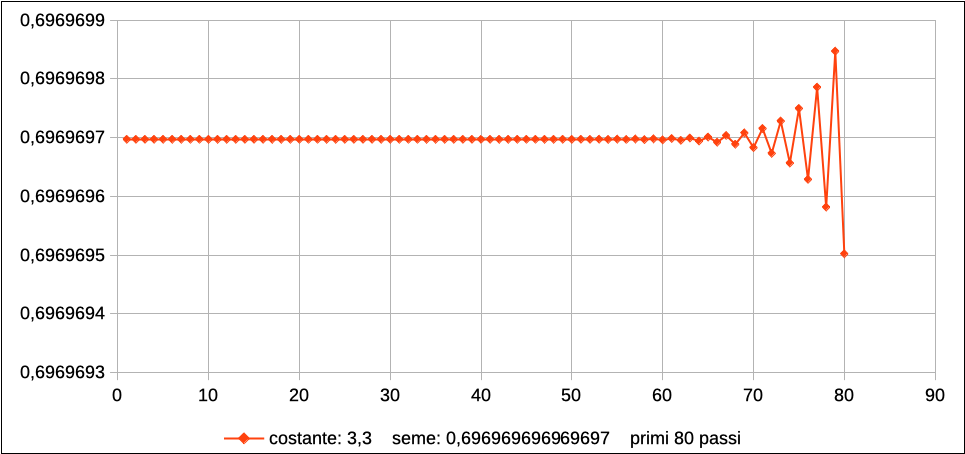
Nell’immagine che segue, una sottile linea rossa rende visibile la traiettoria del valore di x da una generazione alla seguente:
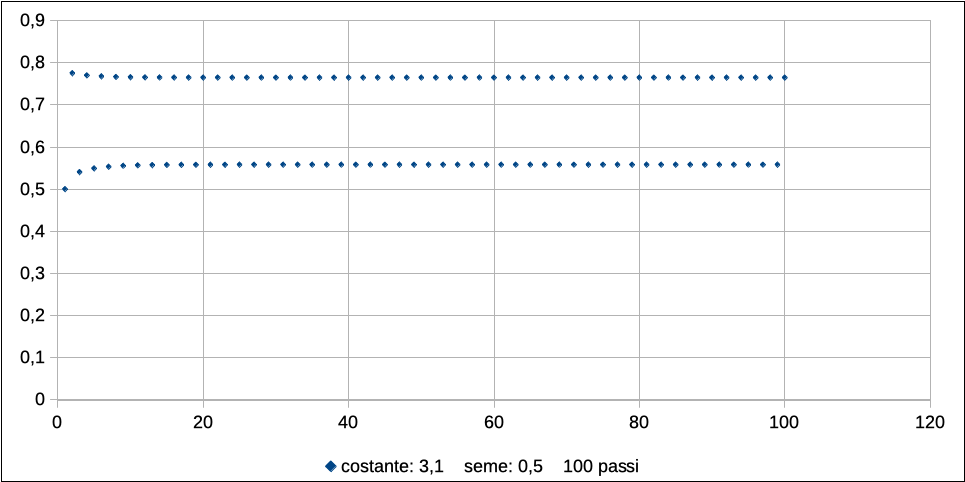
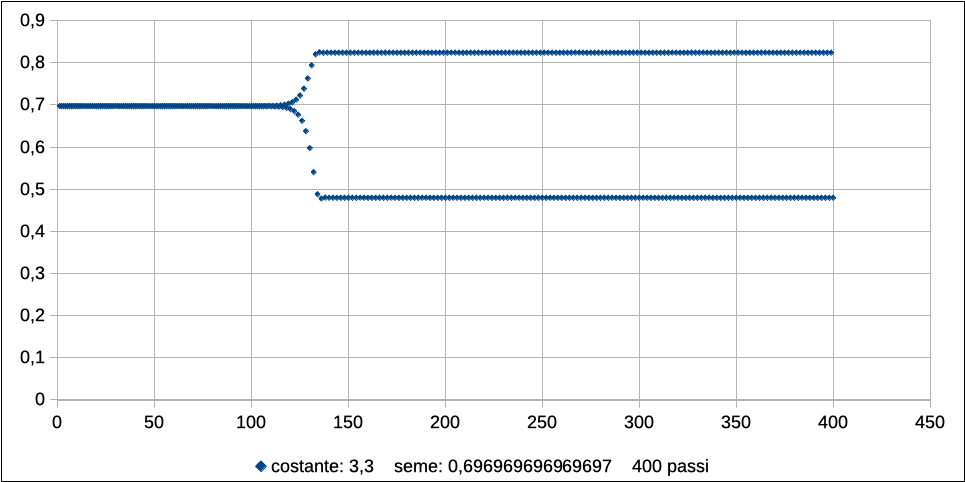
Non appena r supera il valore di 3, si evidenzia subito la nuova condizione di stabilità, con l’oscillazione tra due valori distinti:
Che fine ha fatto la prima radice dell’equazione?
Ci si ricorderà che nell’equazione di stabilità le soluzioni per r erano 3, mentre l’immagine appena riportata ne mostra solo due.
Per scoprire la terza occorre far partire la traiettoria da un valore iniziale pari proprio alla terza soluzione (1 – 1/r) e da un valore di r un po’ più alto:
Il sistema parte proprio dal punto di stabilità 1 – 1/r, ma basta una piccola perturbazione dovuta alla precisione per forza di cose limitata del foglio di calcolo, per portarlo via da questo punto di stabilità, verso l’oscillazione tra gli altri due valori di stabilità.
Il punto 1 – 1/r è quindi un punto di equilibrio instabile.
Cosa ci racconta questo scenario?
Quando il tasso di crescita supera il limite sostenibile, è ancora possibile che il sistema trovi una sua stabilità con generazioni numericamente uguali una all’altra. Ma è una stabilità precaria, una qualunque perturbazione delle condizioni operative spingerà infatti il sistema verso un nuovo equilibrio, dove una generazione su due sottrae risorse alla prossima.
Logistic map: ancora qualche passo verso il disordine
È ovviamente ipotizzabile che il sistema possa raggiungere una stabilità oscillando tra più di due determinati valori.
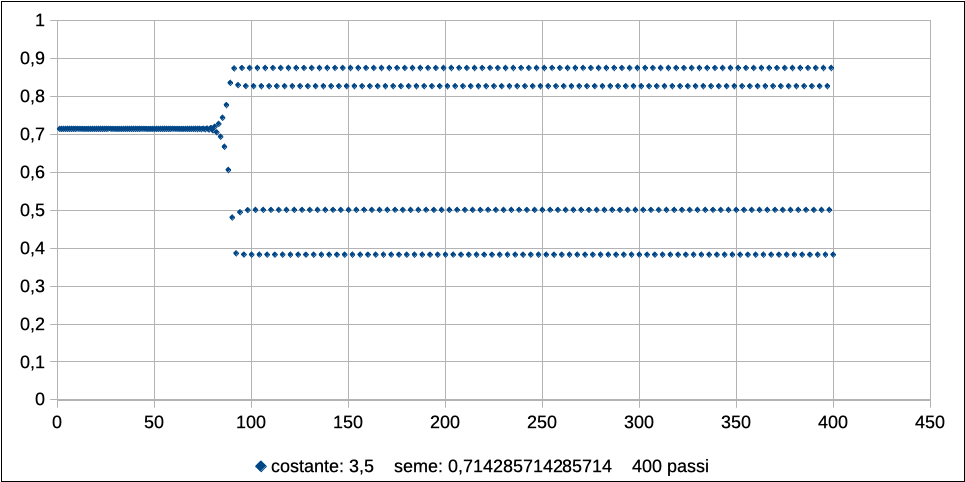
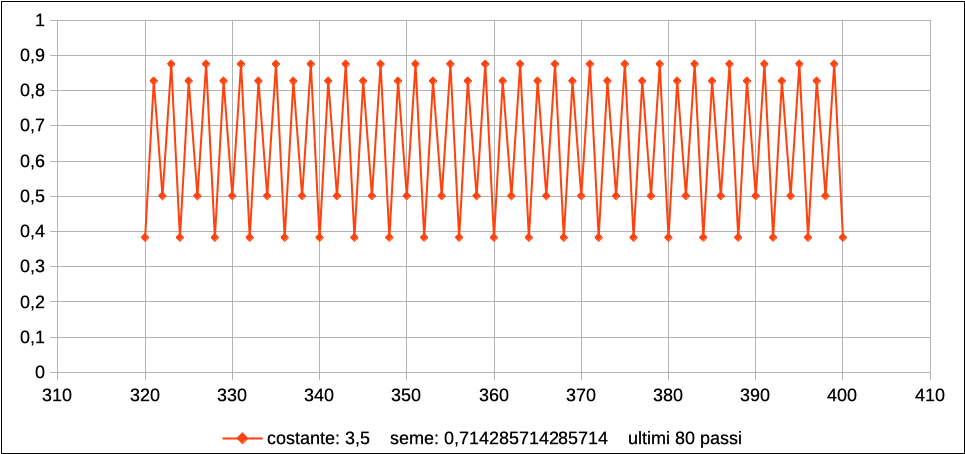
Abbandonando la strada della soluzione algebrica, troppo complessa, possiamo provare ad aumentare ancora il valore di r, sempre però facendo partire la traiettoria dal valore di equilibrio instabile di 1 -1/r. Ecco, ad esempio, il caso di r = 3.5:
A regime il sistema oscilla stabilmente tra quattro valori:
Veloci verso il caos
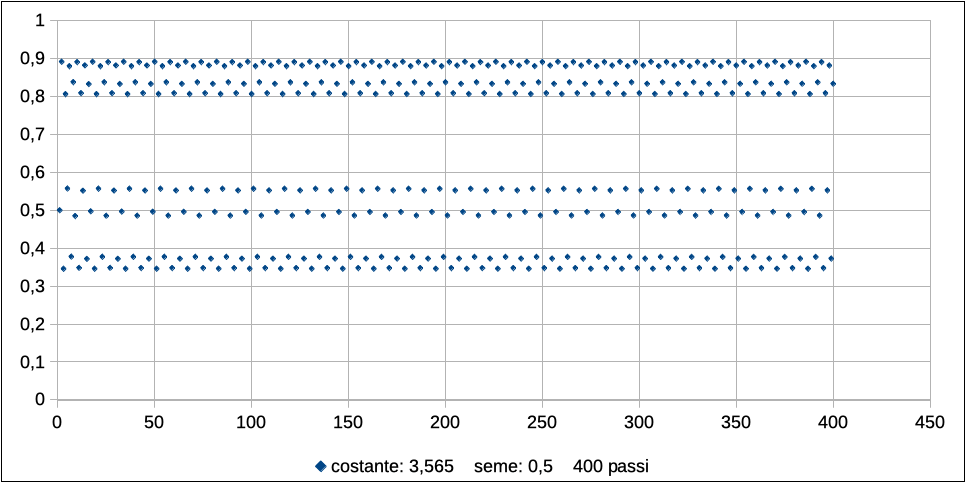
Aumentando ancora il valore del tasso di riproduzione r, si arriva a ulteriori sdoppiamenti progressivi dei punti di stabilità:
Fino a che, avvicinandosi sempre più al valore limite di 4, il numero di sdoppiamenti rende impossibile scorgere un ordine nella sequenza dei punti attraversati dalla traiettoria.
In questo ultimo caso, partendo dal solito punto di equilibrio instabile 1 – 1/r, si nota la partenza in equilibrio, poi abbandonata dopo alcune decine di generazioni.
Il modello dinamico di Robert May dovrebbe farci riflettere sugli effetti della mancanza di solidarietà tra generazioni, quando si tratta di utilizzo delle risorse del pianeta.
Si guardi, ad esempio, il caso di r = 3.3, con l’oscillazione, della popolazione tra il 50% e l’80% circa della capacità totale del pianeta e si pensi a quali conseguenze sociali deriverebbero da un crollo della popolazione dall’80% al 50%, da una generazione all’altra.
Ma anche l’illusoria stabilità del caso r = 3.95 non sarebbe da meno, con la successiva, rapida e improvvisa caduta nel caos più assoluto.
L’immagine di apertura dell’articolo è di Gerd Altmann, da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.