L’ago di Buffon e pi greco

L’ago di Buffon e la sua relazione con pi greco mi hanno sempre intrigato. Di cosa si tratta?
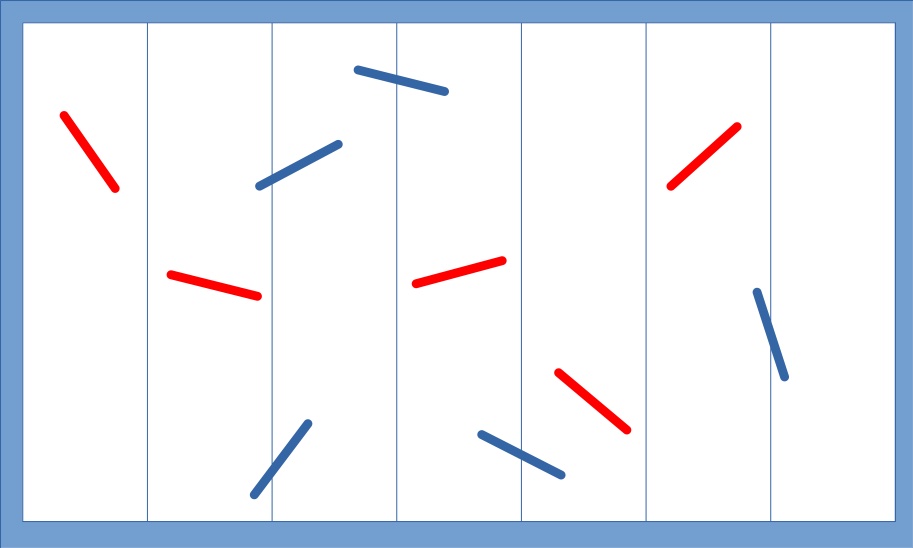
Si immagini di tracciare su un foglio bianco delle linee parallele (orizzontali o verticali), equidistanti tra loro. Si lasci ora cadere a caso un ago sul foglio. Qual è la probabilità che l’ago tocchi almeno una delle linee parallele? Nel 1777 lo scienziato francese Georges-Louis Leclerc, conte di Buffon, trovò che questa probabilità si esprime in termini di pi greco.
Dalla stessa relazione matematica si può quindi ricavare una stima di pi greco, se si conosce la probabilità in questione. E la probabilità si può stimare ripetendo un sufficiente numero di volte l’esperimento della caduta dell’ago sul foglio.
Ecco, è con quel sufficiente che mi scontro da un po’ di anni, ogni qualvolta, cioè, non avendo di meglio da fare, mi metto a giocare con l’ago di Buffon.

L’ago di Buffon e pi greco: la formula

Una buona trattazione del tema si trova su Wikipedia. In estrema sintesi, se si indica con P la probabilità che l’ago tocchi almeno una linea, con t la distanza tra le linee e con l la lunghezza dell’ago, e se l ≤ t, allora: P = 2 l / t π.
Rovesciando la relazione, si può esprimere π in termini di P: π = 2 l / t P.

Da qui l’esperimento: se lascio cadere un numero di volte N l’ago sul foglio e conto le volte C che l’ago tocca una linea, allora posso approssimare P con C / N (Probabilità = casi_favorevoli / casi_totali).
La questione è: quante volte devo lanciare l’ago, per essere sicuro di avere una stima di pi greco con almeno 3, 4, 5, … cifre esatte?

Nota: l’esperimento di Buffon ha poi aperto la strada all’applicazione del Metodo Monte Carlo, che basa la risoluzione (approssimata) di problemi complessi da risolvere per altra via, sulla simulazione numerica di un esperimento con una variabile casuale.

In rete si trovano moltissime pagine con simulazioni dell’ago di Buffon realizzate con diversi linguaggi di programmazione, ma non molto circa la precisione ottenibile con l’esperimento. Dal canto mio, ho provato a suo tempo con il Basic, poi con Excel, adesso con Python. Ma niente, anche spingendo il numero di lanci a qualche centinaio di milioni, la precisione nel calcolo di pi greco mi sembra lasci a desiderare. All’aumentare del numero di lanci, lo scostamento della stima dal valore esatto di π non decresce con regolarità, ma presenta un andamento a sussulti.

Il primo programma

Complice la mia pigrizia, sono partito scegliendo l = t, che è al limite della validità della formula, ed ho simulato ciascun lancio estraendo due numeri casuali: il primo tra 0 e 1, che rappresenta l’ascissa della base dell’ago, il secondo tra 0 e 360 gradi, che rappresenta la rotazione dell’angolo, rispetto alla linea orizzontale.
A completare le ipotesi, ho immaginato che sul foglio fossero tracciate linee verticali, poste a una distanza 1 tra loro.

L’esperimento consiste quindi nella simulazione di 500 pacchetti, ciascuno di 500.000 lanci. Alla fine di ogni pacchetto viene stimato il valore di pi greco desunto dai risultati dei lanci e quello cumulativo desunto da tutti i pacchetti di lanci effettuati fino a quel punto. Mi aspetto che quest’ultima stima si avvicini rapidamente al valore 3.14159… di pi greco.

All’esecuzione di ciascun pacchetto di simulazione, il programma stampa una riga di valori separati da una virgola. Le 500 righe vengono poi importate in un foglio di calcolo (Excel o LibreOffice Calc), da cui è molto semplice ricavare i grafici di sintesi dell’esperimento.

Ecco com’è andata

I 4 grafici qui sotto rappresentano, nell’ordine:

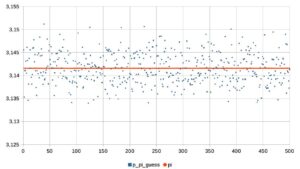
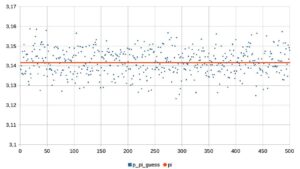
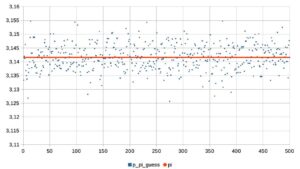
• la stima di pi greco ricavata da ciascun pacchetto di lanci; come si vede, i valori cadono tutti in un intorno del valore di pi greco (linea rossa);
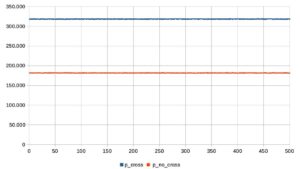
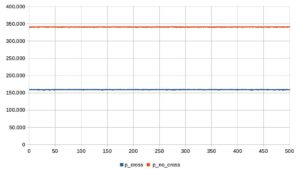
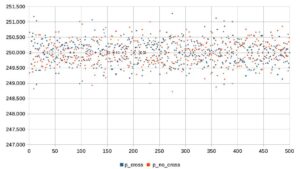
• il numero di lanci in cui l’ago incrocia una linea (in blu) e quello in cui l’ago non incrocia nessuna linea (in rosso); i valori relativi ai vari pacchetti sono tutti molto vicini, rispettivamente, a 318.000 e 182.000;
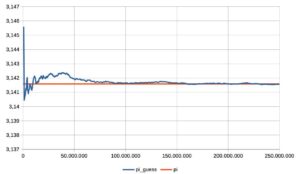
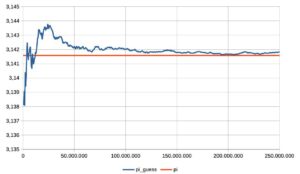
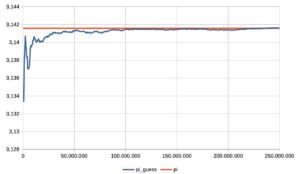
• la stima cumulativa di pi greco; dopo aver raggiunto una buona approssimazione verso i 100.000.000 lanci, successivamente ci sono dei sussulti, invece dell’attesa approssimazione via via più precisa;
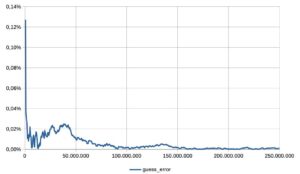
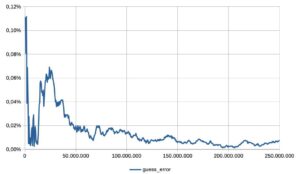
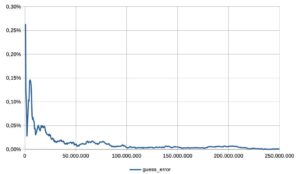
• il fenomeno è evidenziato dal quarto grafico, che riporta l’errore assoluto della stima rispetto al valore di pi greco.

Il secondo programma

A questo punto sono andato in cerca di suggerimenti in rete. Ne ho trovati due.

Primo: tenersi lontani dalla condizione limite: l = t. Ho visto che la scelta più diffusa è che la lunghezza dell’ago sia la metà della distanza tra le linee, e ho seguito questa impostazione.

Secondo: nei modelli di simulazione che ho trovato, dei due parametri casuali che determinano il punto di caduta dell’ago, il primo indica non un estremo dell’ago, come nel mio primo programma, ma il centro dell’ago stesso. Non so quanto questo influisca sulla bontà della simulazione, ma ho modificato la mia implementazione dell’algoritmo in questo senso.

Risultato? Siamo lì, di seguito i grafici di una simulazione con risultati non particolarmente brillante.

Da notare nel secondo grafico che si è invertita la posizione tra le linee che riportano il numero di lanci che incrociano una linea (in blu) e il numero dei lanci che non incrociano una linea (in rosso). Essendo diminuita la lunghezza dell’ago, è meno probabile avere incroci.

Il codice in Python

Per chi fosse interessato, ecco il codice di questa seconda versione del programma.

# simulazione del lancio dell'Ago di Buffon
# 6set21, by p.p.
import random
import math
n_pacchetti = 500
dim_pacchetti = 500000
l_ago = 0.5
#
cross, no_cross = 0,0
for pacchetto in range(1,n_pacchetti+1):
    p_cross, p_no_cross = 0,0
    for i in range(1,dim_pacchetti+1):
        x = random.uniform(0.0, 1.0)
        alpha = random.uniform(-math.pi/2, math.pi/2)
        x0 = x - 0.5 * l_ago * math.cos(alpha)
        x1 = x + 0.5 * l_ago * math.cos(alpha)
        if x0>0 and x1<1:
            p_no_cross += 1
        else:
            p_cross += 1
    p_pi_guess = dim_pacchetti * 2 * l_ago/p_cross
    cross += p_cross
    no_cross += p_no_cross
    pi_guess = pacchetto * dim_pacchetti * 2 * l_ago/cross
    guess_error = abs(pi_guess - math.pi)/math.pi
    print (p_cross, ",", p_no_cross,",",p_pi_guess,",",cross,",",no_cross,",",pi_guess,",",guess_error)

Il terzo programma

Ultima ispirazione: utilizzare una lunghezza dell’ago tale da rendere ugualmente probabili l’incrocio e il non incrocio di una linea.

Questo si ottiene facilmente dall’espressione P = 2 l / t π,  ponendo P = 1/2. L’ago deve risultare di lunghezza l/t = π/4.
Basta quindi modificare una linea del programma:

l_ago = math.pi / 4

Niente, nemmeno questa mossa cambia granché. La curva dell’errore presenta ancora sussulti, al posto di un andamento regolarmente decrescente.

Da notare, nel secondo grafico, che effettivamente i due eventi incrocio e non incrocio sono diventati equiprobabili. La scala delle ordinate, infatti, si è ridotta al punto di poter distinguere i punti relativi ai singoli lanci.

Cosa aggiungere? Anche stavolta la simulazione dell’ago di Buffon mi nasconde il segreto dell’andamento della rapidità di convergenza a  π, sempre che non abbia inserito qualche sciocchezza nel codice. Dovrei sicuramente ripassare il libro di statistica, o cercare meglio in rete. Da qualche parte qualcuno avrà già risposto alla mia domanda.

Pasquale

Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it