La scimmia instancabile dà il nome a un paradosso della statistica, in cui sono inciampato quando ero ancora studente di ingegneria:
“Qual è la probabilità che una scimmia, battendo a caso i tasti di una macchina da scrivere, riproduca il testo dell’Amleto di Shakespeare?”
La qualifica di instancabile la scimmia se la merita tutta perché, come vedremo e come è intuibile, bisognerebbe attendere un tempo incredibilmente lungo per veder emergere dai fogli dattiloscritti la tragedia di Amleto. Le leggi della statistica ci dicono infatti che la probabilità di un tale evento è maggiore di zero, e che quindi prima o poi l’evento si verificherà, pur di attendere abbastanza tempo.
Con l’aiuto di un po’ di statistica di base e qualche riga di codice cerchiamo di realizzare quanto è questo abbastanza.
La scimmia instancabile alla tastiera
Nei primi anni ’70, studente di ingegneria, trovai nella libreria di mio padre il volumetto Il mondo dei grandi numeri, di Philip J. Davis, edito da Zanichelli.
Un tascabile di nemmeno 200 pagine che tratta in modo chiaro e divertente del calcolo numerico, aiutando a destreggiarsi tra i numeri, grandi o piccoli, che ci creano disagio quando li incrociamo nella nostra vita.
Non mi risultano edizioni successive a quella della copia in mio possesso, pubblicata nel 1965 (l’originale in inglese è del 1961), ma il manualetto è ancora attuale, fresco e godibile.
Un capitolo divertente riguarda la rude arte della stima: come si fa a stimare il consumo annuo di panini imbottiti in Europa?
Il capitolo centrale riguarda, come si può intuire dalla copertina, la storia del pi greco, naturalmente fino al 1961. La crescita esponenziale della potenza di calcolo consentirà poi di frantumare ogni record di conoscenza delle cifre di pi greco.
Nell’appendice si trovano alcuni numeri estremamente piccoli o grandi, con il riferimento alla situazione in cui li si può incontrare.
Uno riguarda appunto la scimmia instancabile ed è la probabilità che riproduca il capolavoro di Shakespeare, battendo a caso sui tasti di una macchina da scrivere.
Ipotizzando una tastiera di 35 tasti (26 lettere dell’alfabeto inglese + qualche segno di interpunzione + spazio), e assumendo che servano 27.000 battute per riprodurre l’Amleto, la probabilità di un evento del genere è di 1 su 3527.000 ≈ 1040.000.
Si tratta di un numero tanto grande da sfuggire alla nostra capacità di stima diretta: si pensi solo che la probabilità di realizzare un 6 al Superenalotto è di 1 su 622.614.630, cioè meno di 1 su 109.
Un modo per stimare il valore di un numero
La probabilità appena riportata ci dice che la scimmia dovrà digitare mediamente 3527.000 volte una sequenza di 27.000 battute, prima di tirar fuori il testo dell’Amleto senza nemmeno un errore.
Quanto tempo bisognerebbe attendere, se la scimmia impiegasse un secondo a battuta?
Il tempo necessario a digitare le 27.000 battute sarebbe poco più di 7 ore, ma bisognerebbe attendere, in media, 3527.000, cioè circa 1040.000 volte 7 ore.
Proviamo a farci un’idea della durata dell’attesa. Quanti secondi ci sono in un milione di anni?
anno = 60*60*24*365.24
milione_di_anni = anno * 1000000
print ('in un anno ci sono {:0.1f} milioni di secondi'.format(anno/1000000))
print ('un milione di anni contiene {:.0E} secondi'.format(milione_di_anni))
in un anno ci sono 31.6 milioni di secondi
un milione di anni contiene 3E+13 secondi
La notazione 3E+13 rappresenta 3 * 1013 , che è meno di 1014, ancora estremamente più piccolo di 1040.000.
Un’attesa decisamente lunga, che P.J. Davis sintetizza affermando che una probabilità minore di 1 su 10500 descrive un evento di impossibilità assoluta.
Il paradosso di Borel
Non sono dello stesso parere le leggi della statistica. O meglio, le leggi della statistica prescindono da concetti come il ragionevole tempo di attesa di un evento: se la probabilità è maggiore di zero, prima o poi l’evento si realizzerà, anzi si realizzerà un’infinità di volte.
È il paradosso di Borel. Si spiega, dice Wikipedia:
“Calcolando il tempo medio di uscita di una stringa, che oltre ad essere estremamente lungo, cresce in base alla sequenza di caratteri ripetuti all’interno della stringa stessa”.
Una semplice simulazione
Ho utilizzato un Google Colab notebook per qualche semplice simulazione sull’argomento. Il notebook è accessibile a questo indirizzo, per poterci giocare occorre autenticarsi con il proprio account Google.
L’ambito modellato è molto semplice: quante volte la nostra scimmia instancabile dovrebbe digitare a caso parole di 4 lettere, prima di azzeccare quella che abbiamo come obiettivo? E se la parola fosse di 5 lettere? Assumo che la tastiera abbia 21 tasti (az = ‘ABCDEFGHILMNOPQRSTUVZ’).
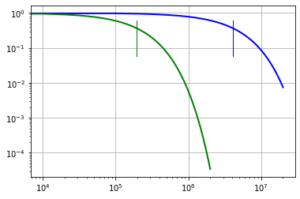
Il grafico qui accanto riporta l’andamento della probabilità di non ottenere la parola voluta dopo un certo numero di tentativi, probabilità ottenuta dalle leggi della statistica (il codice Python è nel notebook).
Il numero di tentativi necessari per arrivare al ginocchio delle due curve, dove, cioè, la probabilità di insuccesso scende al di sotto del 50%, è minore di un milione per una parola di 4 lettere e di 10 milioni per una parola di 5 lettere.
È però possibile in modo abbastanza semplice simulare la digitazione effettiva. Sempre nel notebook è riportato il codice per il caso di 4 e quello di 5 lettere.
Per velocizzare il tempo di esecuzione, ho creato una lista di 25 parole da 4 lettere e una di 20 parole da 5 lettere. In entrambi i casi sono presenti 100 lettere, che riportano con ragionevole approssimazione la frequenza delle lettere nella lingua italiana. Non è un elemento che influisca nel calcolo, o almeno così mi pare. Potrei giustificare questa scelta con un mix di senso estetico e di puro paraculismo.
Il codice è semplice, si veda il caso delle parole di 5 lettere:
from random import randint
az = 'ABCDEFGHILMNOPQRSTUVZ'
word = ['SCAVO','PESCA','LIANA','RUOTA','MOLLE']
word += ['LORDA','TORNO','VAGHI','PANNO','BIDET']
word += ['TIZIE','FIGLI','ACQUA','CHELE','RESTO']
word += ['BREVI','FORME','MESTE','QUASI','ZINCO']
num_ok = 0
for n in range(1,20000001):
guess = az[randint(0,20)]+az[randint(0,20)]+az[randint(0,20)]+az[randint(0,20)]+
az[randint(0,20)]
if guess in word:
print ('trovata la parola {} in {} tentativi'.format(guess,n))
num_ok += 1
print ('-----')
if num_ok == 0:
print ('dopo {} tentativi non sono riuscito a trovare nessuna delle parole:\n {}'
.format(n,word))
else:
print ('trovate {} parole dopo {} tentativi'.format(num_ok,n))
L’esito della simulazione
Il programma cicla su 20 milioni di tentativi, equivalenti a 400 milioni di tentativi, se si considera che l’evento si realizza per una qualunque delle 20 parole del dizionario.
Bene, l’esito del programma è come riportato:
trovata la parola CHELE in 34006 tentativi
trovata la parola ZINCO in 209178 tentativi
trovata la parola SCAVO in 289329 tentativi
trovata la parola SCAVO in 340536 tentativi
trovata la parola ZINCO in 415709 tentativi
...
trovata la parola ZINCO in 19590419 tentativi
trovata la parola BIDET in 19975556 tentativi
-----
trovate 98 parole dopo 20000000 tentativi
Nota: le parole ZINCO e SCAVO sembrano eccessivamente frequenti nel frammento di output pubblicato. Le altre parole recuperano nel listato completo.
Quindi, nell’equivalente di 400 milioni di tentativi la parola obiettivo è stata trovata circa 100 volte. In media una volta ogni 4 milioni di tentativi.
Qual era il valore atteso? La probabilità di indovinare una parola di 5 lettere digitate a caso su una tastiera di 21 lettere è pari a: (1/21)5, equivalente ad affermare che, per vedere un evento positivo, occorre attendere 215 tentativi = 4.084.101.
Quanto tempo occorrerebbe, in media, per vedere uscire una singola parola corretta da 5 lettere? 4.000.000 di parole da 5 battute sono 20.000.000 di battute. A una battuta al secondo fanno 20.000.000 di secondi. Abbiamo visto che in un anno ci sono circa 31 milioni di secondi, quindi l’operazione richiederebbe i 2/3 di un anno, cioè 8 mesi.
Andrebbe comunque considerato l’impegno necessario a verificare cosa scrive la scimmia, per poter gridare “Eureka!” al momento giusto.
Una contro-verifica si ha esaminando il caso di parole da 4 lettere. In questo caso il codice effettua 2 milioni di tentativi con un dizionario di 25 parole, equivalenti a 50 milioni di tentativi. Bene, nella simulazione la scimmia indovina 263 parole, con un numero di circa 190.000 tentativi a parola.
La probabilità ci dice che occorre attendere in media 214 tentativi, pari a 200.000 tentativi.
In sintesi
La scimmia instancabile mi ha fatto ritornare indietro di un bel po’ di anni, a quando cominciavo a prendere dimestichezza con gli strumenti pratici e logici dell’ingegneria: il regolo, la stima delle grandezze, la simulazione di eventi. A parte il regolo, rapidamente sorpassato dalla calcolatrice proprio in quegli anni, e poi dal pc, gli altri due strumenti mi hanno effettivamente accompagnato in tutta la vita lavorativa.
E, a proposito di cammino dal regolo alla programmazione, oggi ci sono strumenti formidabili per avvicinarsi alla programmazione. Google Colab è giusto uno dei tanti, immediatamente e gratuitamente disponibile a chiunque abbia un account Google.
Nell’immagine di apertura, di Gerhard G. da Pixabay, la scimmia instancabile sta scegliendo il prossimo libro da trascrivere.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.