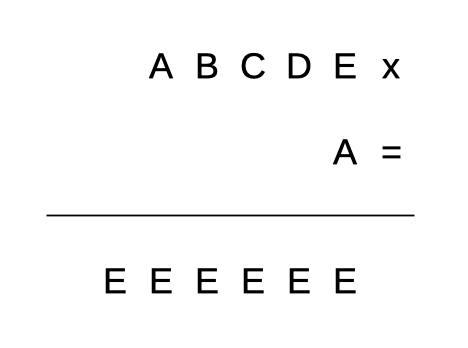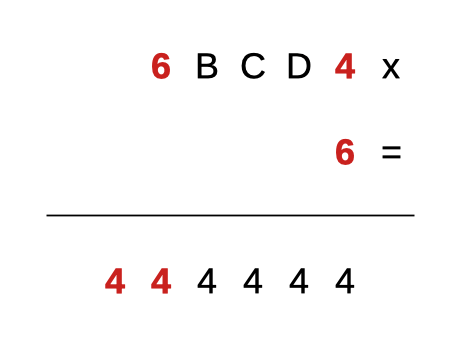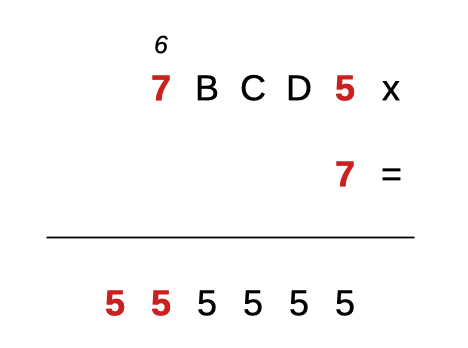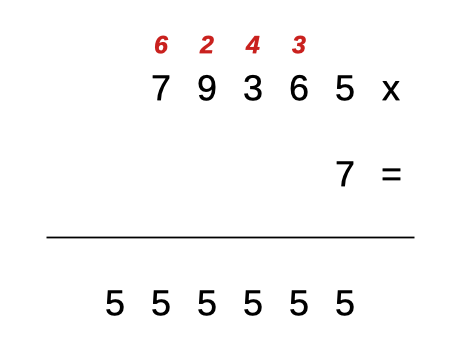Mi capita, di tanto in tanto, di imbattermi in un criptarisma, cioè in un calcolo in cui le cifre si nascondono dietro delle lettere: a lettera uguale corrisponde cifra uguale e, per converso, a lettere diverse corrispondono cifre diverse. Per risolvere un criptarisma occorre ricorrere alla criptaritmetica (o criptoaritmetica), vale a dire all’arte di dedurre e rendere visibile il calcolo nascosto, con ragionamenti logici rigorosi.
Questa volta l’incontro avviene sulla rivista Popularmechanics.com, che racconta di come un test destinato a bimbi taiwanesi di 9 anni sia risultato ostico tanto per gli allievi quanto per gli insegnanti:
ABCDE è un numero di cinque cifre diverse tra loro e che, moltiplicato per la sua prima cifra A, dà come risultato il numero di sei cifre tutte uguali all’ultima, E.
Vediamo come l’ho risolto io e come, in modo molto più semplice e ingegnoso, è stato risolto da Presh Talwalker sul suo canale YouTube.
Nota: in queste pagine si era già parlato di criptaritmetica, nell’articolo Ginnastica per la mente: il FridayPuzzle su Twitter.
Criptaritmetica: primi passi
Il primo passo è forzatamente guardare sul lato destro della moltiplicazione.
A non può valere 1, naturalmente, quindi sarà una cifra da 2 a 9 compresi. Dobbiamo poi trovare la coppia di cifre A ed E distinte che, moltiplicate tra loro, danno un numero che finisce con E. Ad esempio: 6 x 4 = 24, “scrivo 4 e riporto 2”.
Un foglio di calcolo (LibreOffice Calc o Excel) ci aiuta con una semplice formula:
Inseriamo cioè nello schema il resto a 10 (vale a dire l’ultima cifra) del prodotto delle cifre E (colonna D) per le cifre A (riga 3). Il segno $ prima della colonna e prima della riga consentono di ricopiare la formula correttamente sull’intera tabella.
La tabella risulta però non leggibilissima:
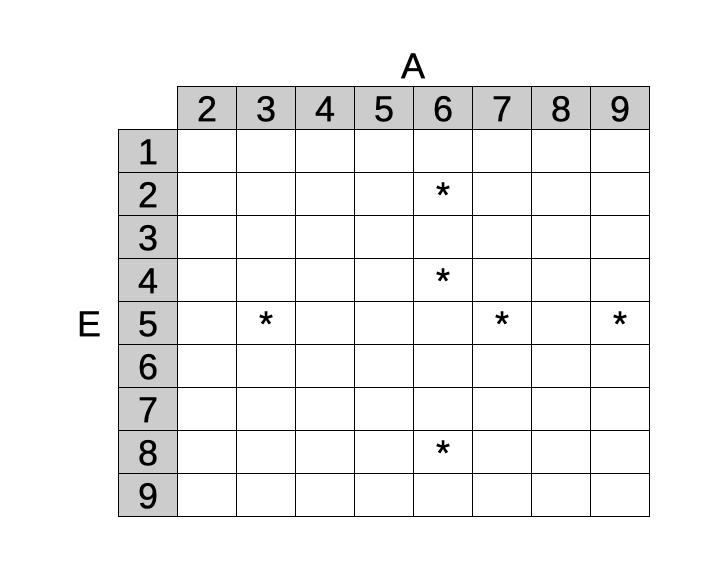
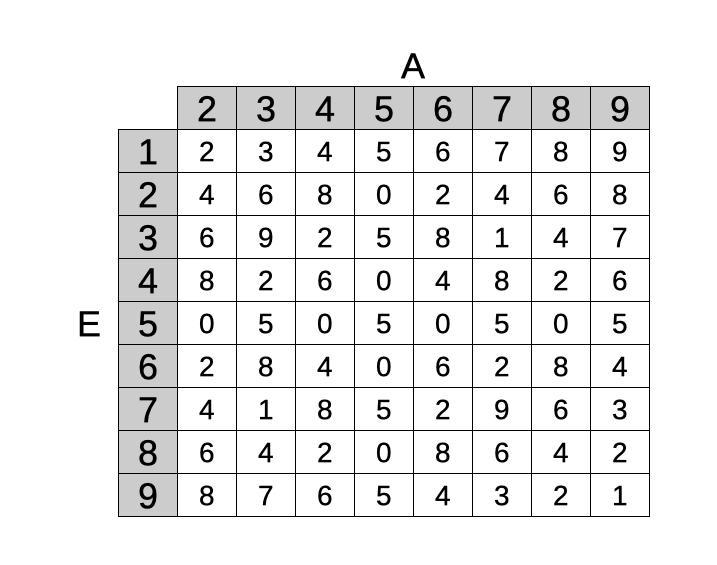Conviene allora mostrare solo le coppie che soddisfano il nostro caso, quelle cioè in cui A ed E sono cifre diverse tra loro e la cifra della tabella è uguale a E.
Abbiamo quindi le seguenti coppie (A,E): (6,2), (6,4), (6,8), (3,5), (7,5), (9,5), tra le quali individuare quella (o quelle) che soddisfano il problema.
Qui le strade divergono
Come vedremo più sotto, Presh Talwalker a questo punto prosegue con un passaggio molto intelligente. Ahimè io ho invece tirato dritto con le deduzioni classiche da criptaritmetica, ragionando a questo punto sul lato sinistro della moltiplicazione.
Il ragionamento è che A x A, più l’eventuale riporto dalla cifra precedente, deve fare EE. Vediamo quale riporto sarebbe necessario per quadrare i conti, per ciascuna delle diverse coppie:
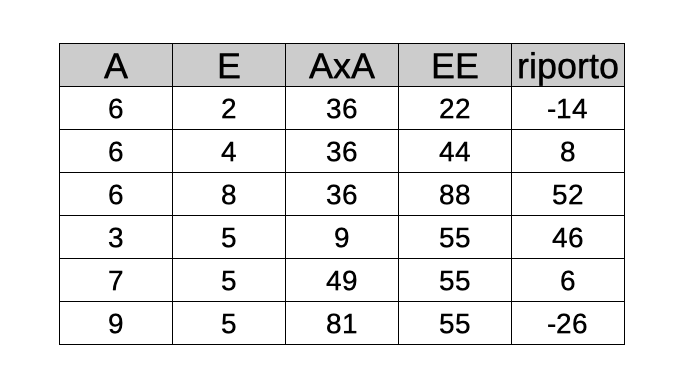Scartati i riporti negativi o impossibili da generare in un prodotto di due cifre, rimangono due coppie (A,E): (6,4) e (7,5).
La prima coppia va scartata, perché porterebbe a questo schema:
Il riporto di 8, necessario per andare da 6 x 6 = 36 a 44, è impossibile da generare con il prodotto B x 6, compreso un eventuale riporto.
Rimane quindi la sola coppia (A,E) = (7,5) e la nostra moltiplicazione comincia a disvelarsi:
Ora si va in discesa!
Perché il prodotto B x 7 dia riporto di 6, B deve valere 9 (9 x 7 = 63, scrivo 3 e riporto 6).
Ma, attenzione, non devo scrivere 3, bensì 5, quindi ho bisogno che C x 7 dia un riporto di 2, cosa possibile se C = 3 (3 x 7 = 21). È da scartare, invece, il caso C = 4, perché 7 x 4 =28, e 8 è maggiore di 5.
Siamo arrivati a C = 3, e quindi 3 x 7 =21, scrivo 1 e riporto 2. Come nel passaggio precedente, non devo scrivere 1, bensì 5, quindi ho bisogno di un riporto di 4, e allora: D = 6 (6 x 7 = 42).
Eccoci arrivati al fondo:
La soluzione è 79365 x 7 = 555555.
Il pensiero laterale!
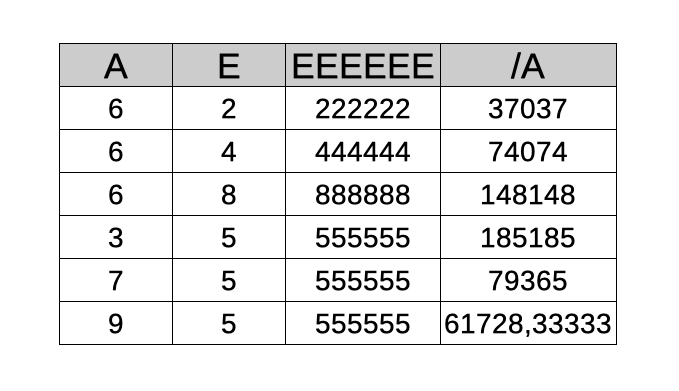
Una volta individuate le coppie possibili (A,E): (6,2), (6,4), (6,8), (3,5), (7,5), (9,5), Presh Talwalker fa un’osservazione fulminante (per me): EEEEEE deve essere divisibile per A (e deve dare ABCDE)!
Da questa tabella è evidente che vanno scartate tutte le righe in cui il rapporto EEEEEE / A non è intero oppure ha cifre che si ripetono (ricordare che ABCDE deve avere sei cifre diverse tra loro).
In un solo passaggio, quindi, rimane la soluzione: ABCDE = 79365!
L’immagine di apertura dell’articolo è di Adriano Gadini, da Pixabay.
Articoli correlati:
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
