Quanti francobolli, al minimo, servono per comporre un’affrancatura di 1,53$, se si hanno a disposizione solo tagli da 5 e 8 centesimi?
A porre la domanda, l’8 novembre 1986, era il Math Contest dell’Università della Carolina del Sud. Un problema nemmeno tanto complesso, che mi è tornato in mente ragionando su quali siano vantaggi e svantaggi di tre differenti approcci alla soluzione di puzzle matematici di questo tipo. Eccoli elencati in ordine decrescente di impegno mentale:
- il metodo carta-penna-ragionamento, per ridurre al minimo i calcoli necessari;
- un foglio di calcolo (es.: Excel) e una manciata di formule, con ragionamento ridotto al minimo;
- qualche linea di codice (es.: Python).
Mi capita di usare tutti e tre i metodi, a seconda della difficoltà concettuale del puzzle. A volte un foglio di calcolo può evidenziare una regolarità che porta a capire il ragionamento per espugnare il puzzle. O, altre volte, semplicemente ci sono troppe soluzioni per pensare di estrarle con carta e penna, o per evidenziarle in un grafico o in una tabella.
Nel seguito ho riassunto i tre metodi, proprio sul problema “Quanti francobolli?“.
Il testo del problema
Cominciamo allora dal testo del puzzle matematico lanciato nel lontano 1986:
If Alma wants to mail a package which requires $1.53 in postage, and has only 5-cent and 8-cent stamps, what is the smallest number of stamps she could use to total exactly $1.53?
(a) 24 (b) 23 (c) 21 (d) 14 (e) none of these
Quanti francobolli? Carta-penna-ragionamento
Il numero minimo di francobolli sarà composto da un certo numero x di francobolli da 8 centesimi e un certo numero y di francobolli da 5 centesimi: 8x + 5y = 153.
Ora, 5y terminerà con la cifra 0, se y è pari, con la cifra 5 se y è dispari. D’atro canto 8x terminerà con la cifra 8, se x vale 1, 6, 11, 16, 21 …, altrimenti terminerà con una delle cifre 6, 4, 2 oppure 0.
Poiché 153, la somma da raggiungere, termina con 3, è evidente che le sole combinazioni ammesse sono y dispari e x con un valore tra 1, 6, 11, 16. Il successivo valore possibile per x (21), porterebbe da solo a una somma di 21*8 = 168 centesimi, superiore a 153.
Il minor numero totale di francobolli si avrà quando x è massimo, quindi con: 16 francobolli da 8 centesimi (16 × 8 = 128) e 5 francobolli da 5 (153 – 128 = 25 = 5 × 5). Totale: 16 + 5 = 21 francobolli.
Quali sono i vantaggi e gli svantaggi di questo approccio?
Pro: è il metodo che dà più soddisfazioni, ci si sente un po’ come Hercule Poirot che stana il colpevole con sottili ragionamenti.
Con: ogni combinazione di dati in ingresso richiede un ragionamento specifico, diverso da caso a caso, almeno in parte. Esempio: se l’obiettivo fosse non 153 centesimi ma 154, allora si dovrebbe ragionare sul fatto che y deve essere pari, quindi che 5x dà un contributo uguale a 0 all’ultima cifra del totale, da cui segue che 8x deve terminare per 4.
Il metodo del foglio di calcolo
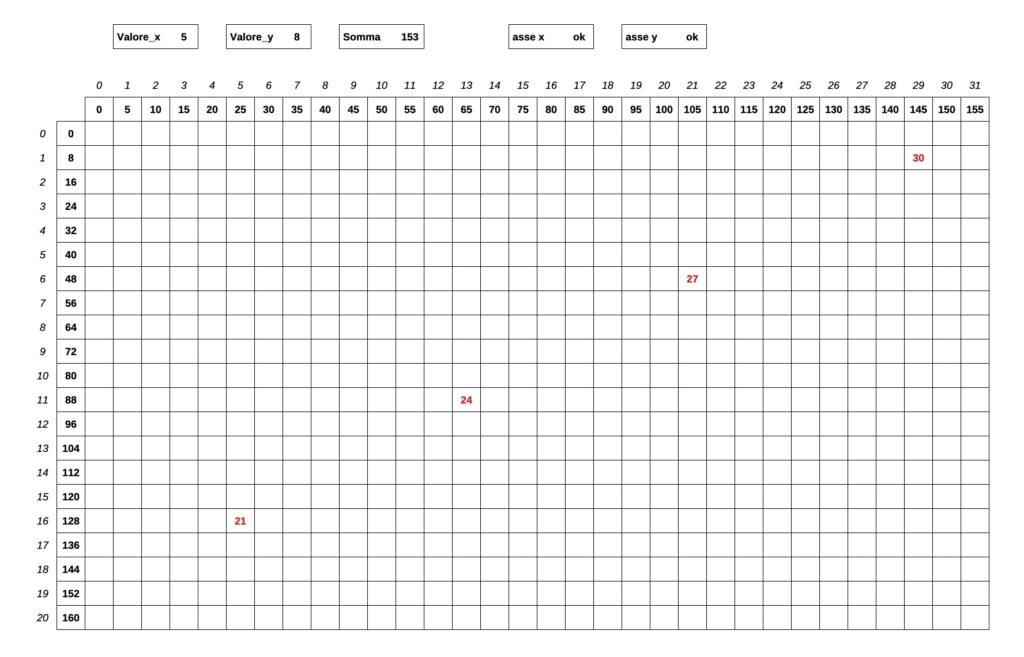
Un modo per utilizzare LibreOffice Calc (o Excel) è quello di preparare un tabellone che riporti nelle due dimensioni il numero progressivo crescente di francobolli da 8 e da 5 centesimi.
Cosa inserire come elementi della tabella? Si può calcolare, in ogni cella della tabella, la somma di 8x e di 5y e poi lasciare la cella vuota, se 8x + 5y non è pari a 153, e visualizzare x + y nel caso contrario.
A questo punto comparirà qualcosa solo nelle celle corrispondenti a una soluzione e sarà facile scegliere quella con il minimo numero di francobolli.
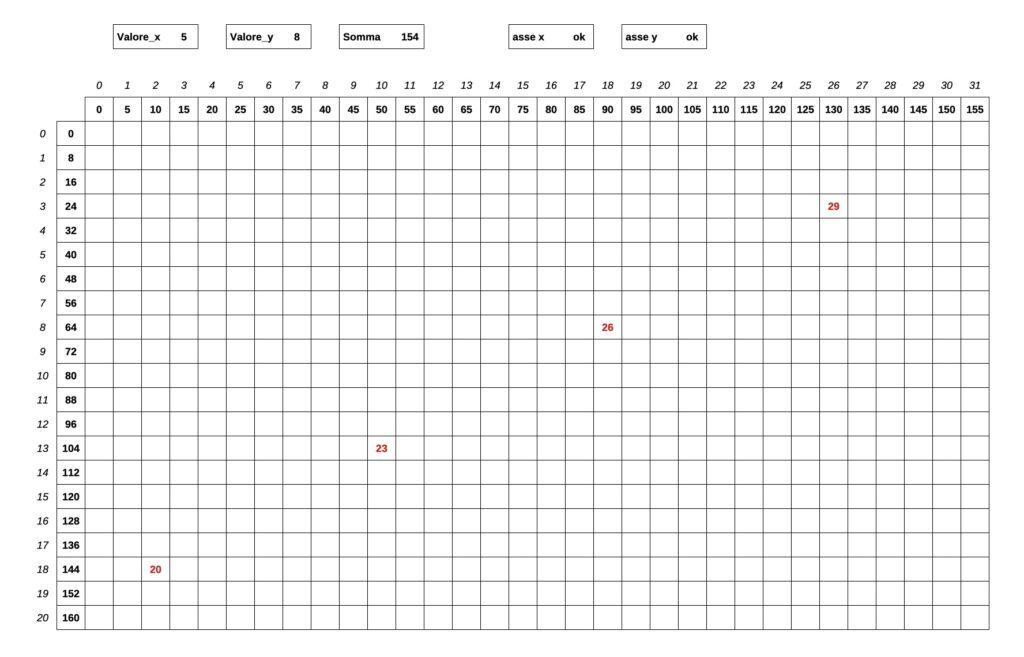
Un vantaggio immediato di questo metodo di attacco al puzzle è la flessibilità: basta cambiare il parametro 153 in 154 per risolvere un caso differente:
Altro vantaggio è l’evidenza grafica che può essere ottenuta: le quattro soluzioni sono disposte su una linea retta, il che è uno spunto a comprendere meglio le fondamenta della questione.
È invece uno svantaggio il dover agire manualmente per regolare la profondità degli assi. Può essere utile inserire dei controlli, come fatto in alto: se il valore del francobollo utilizzato per l’asse x diminuisce sotto una certa soglia, nasce l’alert che chiede di aggiungere colonne. Lo stesso vale per l’altro asse.
Rimane la seccatura di adattare gli assi.
Un altro svantaggio da considerare è che non è necessario alcuno spunto brillante, alla soluzione si arriva semplicemente esplorando tutti i casi possibili.
Meglio due righe di codice?
Il terzo metodo prevede di risolvere il puzzle con qualche riga di codice. Ho utilizzato Python.
# Qual è il numero minimo di francobolli da 8 e da 5 centesimi di euro, per un'affrancatura da 1,53 €?
#
a,b = 5,8
t = 153
min,f = int(153/min(a,b))+1,0
na = 0
while not( a*na > t):
nb = 0
s = na * a
while not(s > t):
if s == t:
print(na+nb,"francobolli,",na, "da",a,"e",nb,"da",b)
if na+nb < min:
min = na+nb
f = 1
nb +=1
s += b
na += 1
if f == 1:
print("Il numero minimo di francobolli necessari per formare",t,"centesimi è:",min)
else:
print("nessuna soluzione")
L’output del programma:
21 francobolli, 5 da 5 e 16 da 8
24 francobolli, 13 da 5 e 11 da 8
27 francobolli, 21 da 5 e 6 da 8
30 francobolli, 29 da 5 e 1 da 8
Il numero minimo di francobolli necessari per formare 153 centesimi è: 21
I vantaggi? Il codice è molto semplice, l’evidenza delle soluzioni è immediata, anche se non esportata in modo graficamente interessante. L’adattamento a diverse condizioni è immediato, basta cambiare una linea di codice (da t = 153 a t = 154) e il resto viene da sé:
20 francobolli, 2 da 5 e 18 da 8 23 francobolli, 10 da 5 e 13 da 8 26 francobolli, 18 da 5 e 8 da 8 29 francobolli, 26 da 5 e 3 da 8 Il numero minimo di francobolli necessari per formare 154 centesimi è: 20
Anche con questo approccio si arriva alla soluzione elencando tutti i casi possibili. Non è vero in generale, a volte è possibile ridurre il campo di esplorazione mediante qualche semplice osservazione. Di fondo, però, non è richiesta nessuna intuizione risolutiva, si elencano le possibili casistiche e si eliminano le non soluzioni.
Dovendo confrontare questo metodo con l’approccio a foglio di calcolo, va rilevato che, per provare diverse condizioni in ingresso, il programma richiede dei passaggi fissi (modifica al testo, salvataggio, nuova esecuzione del programma), mentre con il foglio di calcolo basta modificare un parametro e osservare il risultato.
Quale metodo seguire? Il primo, carta-penna-ragionamento, è quello che dà più soddisfazione ed è anche quello più facile da raccontare. Capita, però, che per tirar fuori il ragionamento corretto sia necessario passare prima da uno degli altri due metodi, che mostrano rapidamente i casi su cui basare il ragionamento figo.
Il codice del programma e il file LibreOffice Calc (ed Excel) sono scaricabili da qui.
Immagine di apertura di Jacqueline Macou da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.