I numeri del 2022

Con l’arrivo di un nuovo anno mi diverto a trovare curiosità matematiche legate alle date che sono in arrivo. Ci saranno date palindrome? Il numero che rappresenta l’anno avrà qualche curiosità che lo distingue dagli altri anni?
Vediamo come si presenta l’anno alle porte, con i numeri del 2022.

I numeri del 2022: ci saranno giorni palindromi?

Una data è palindroma se la sequenza delle sue cifre è identica, sia che la si legga da sinistra a destra che da destra a sinistra. Per ampliare le possibilità si possono considerare diversi formati di data: 03-01-2022, ma anche 3-1-2022 oppure 3-1-22.
Ora, se si scrive un 2022 a rovescio davanti a 2022 e si inseriscono opportuni trattini nella stringa, si ha una data palindroma:

22-02-2022

Se si utilizza invece il terzo formato data:

22-x-22

dove x può assumere tutti i valori possibili con una cifra: 22-1-22, 22-2-22, …, 22-9-22 o il valore 11: 22-11-22.
Niente di eccitante, qualcosa di simile è capitato anche quest’anno: 12-02-2021, 12-1-21, …

Teniamo allora a mente questa data: 22 febbraio 2022 sarà un giorno palindromo. Chissà se il Corriere ne parlerà anche quest’anno, dopo aver celebrato il giorno palindromo del 2021.

Potenze in azione

È più grande 20²² o 22²⁰? Proviamo a verificarlo, senza esplicitare il calcolo.

22²⁰ / 20²² = (22/20)²⁰ / 400

Ora: (22/20)²⁰ = ((1 + 1/10)¹⁰)² e la quantità (1 + 1/10)¹⁰ è minore della costante di Eulero e, definita come il limite per n che tende all’infinito di (1 + 1/n)ⁿ.
Quindi il rapporto cercato è minore di: e² / 400 = (2,71828…)² / 400 = 7,389… / 400 < 1.

Ne segue che 20²² è maggiore di 22²⁰. Ma, se proprio si vuole toccare la cosa con mano, allora basta un piccolo ciclo di istruzioni per tirar fuori che:

20 alla 22 = 41943040000000000000000000000
22 alla 20 = 705429498686404044207947776

I numeri del 2022: giochiamo con le potenze

Un’altra curiosità legata al numero che esprime l’anno che verrà riguarda la possibilità di esprimere questo numero come somma o differenza di quadrati.

Una verifica rapida è praticabile per la differenza di quadrati.
Se 2022 = a² – b², allora si potrà scrivere anche 2022 = (a + b) × (a – b). Quindi 2022 dovrà essere scomposto nel prodotto di due fattori, cosa possibile dal momento che 2022 = 2 × 3 × 337.
Ma, c’è un ma. Se i due fattori sono f₁ e f₂, allora dovrà essere:

a + b = f₁
a – b = f₂

Da cui segue: 2a = f₁ + f₂.

Un pizzico di logica

Il numero 2a è pari, quindi f₁ + f₂ dovrà essere anch’esso pari, cosa possibile solo se f₁ e f₂ sono entrambi pari o entrambi dispari. Ma se 2022 = 2 × 3 × 337, il fattore 2 dovrà essere da una parte, che sia f₁ o f₂, mentre l’altra sarà dispari. Quindi non sarà possibile esprimere 2022 come differenza di due quadrati.
Lo stesso destino toccherà al 2026, mentre tutti gli altri anni del decennio in corso, dal 2020 al 2029, potranno essere espressi come differenza di due quadrati, e diversi lo saranno anche in più modi:

Esprimere 2022 usando una sola cifra

I numeri del 2022: e i venerdì 17?

In un anno possono esserci da 1 a 3 giorni targati venerdì 17. Le combinazioni possibili sono, per un anno non bisestile, il 17 di una di queste combinazioni di mesi:

• maggio;
• giugno;
• agosto
• gennaio, ottobre;
• aprile, luglio;
• settembre, dicembre;
• febbraio, marzo, novembre.

Per un anno bisestile, invece, le combinazioni sono un po’ diverse, avremo il venerdì 17 in una delle seguenti combinazioni:

• maggio;
• giugno;
• ottobre;
• febbraio, agosto;
• marzo, novembre;
• settembre, dicembre;
• gennaio, aprile, luglio.

Essendo la durata dei mesi in giorni costante di anno in anno, le varie situazioni dovrebbero presentarsi con regolarità ciclica “breve”, se non fosse per gli anni bisestili che allungano di parecchio lo schema.
Quando capita un anno bisestile? Un anno è bisestile se è divisibile per 4, purché non sia l’anno che termina un secolo (es.: 1800, 1900). In questo caso l’anno sarà bisestile solo se è divisibile per 400 (es.: 2000).

Quindi il ciclo attuale, cominciato con il 1901, proseguirà immutato fino al 2099 e presenta questa ripetizione:

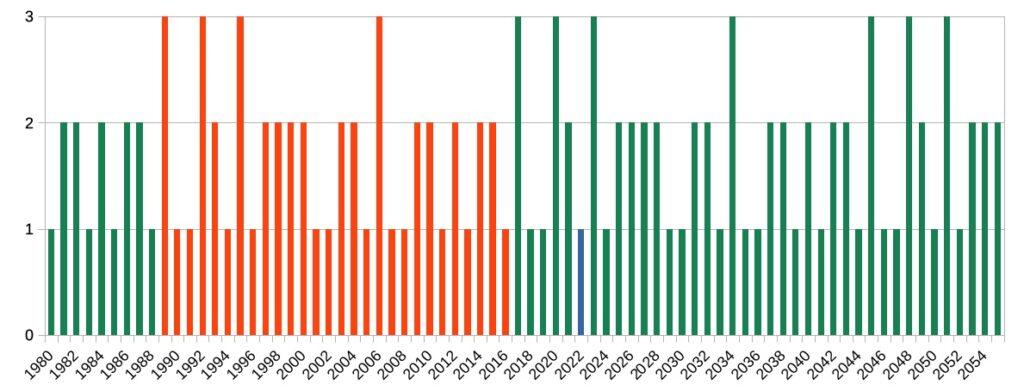
Il ciclo si sviluppa cioè su 28 anni, presentando 4 anni con 3 venerdì 17, 12 con 2 giornate sfigate e i restanti 12 con un solo venerdì 17. Uno di questi ultimi 12 fortunati è il 2022, che avrà solo venerdì 17 giugno.
Non male, se si pensa che veniamo da un 2020 con 3 venerdì 17 e un 2021 con 2. Speriamo che sia di buon auspicio; ma attenzione, il 2023 tornerà ad averne 3.

Un anno noioso?

A giudicare dai numeri del 2022, l’anno in arrivo si presenta come un anno matematicamente noioso.
Devo dire che i suoi predecessori, il 2020 e il 2021, hanno fatto di tutto per risultare tutt’altro che noiosi, direi piuttosto che hanno profuso ansia a piene mani, tra contagi e varianti. Quindi un anno noioso non ci starebbe male.

Non rimane allora che mettersi in attesa che il 2022 arrivi e che palesi una bella noiosità stabile e duratura. Facciamo partire il conteggio alla rovescia:

(9 × 8 × 7 – 6 + 5) × 4+3²+1⁰ = 2022

E che il Cielo ce la mandi buona.

Immagine di apertura di Alexandra Koch da Pixabay.

Pasquale

Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it