
L’equazione di Leonardo mi riporta ai primi mesi del 1973 quando, studente di Ingegneria Elettronica al Politecnico di Napoli, ebbi per la prima volta accesso a un elaboratore (si chiamavano così allora) del centro di calcolo della facoltà.
Il compito da eseguire era abbastanza semplice, d’altra parte era la prima vera esperienza di coding: generare un algoritmo che fornisse un’approssimazione della soluzione reale dell’equazione di terzo grado:
x3 + 2x2 + 10x = 20
universalmente nota come Equazione di Leonardo.
Non si tratta di Leonardo da Vinci, come probabilmente verrebbe istintivamente da pensare, ma di Leonardo da Pisa, meglio noto come Fibonacci, che tutti associamo alla sequenza di numeri di Fibonacci.
Il linguaggio da utilizzare era il Fortran, se non ricordo male la versione Fortran IV.
Del mio codice non ricordo nulla; ricordo molto bene, invece, l’ansia tra il momento della consegna delle schede perforate sul vassoio di input e il ritiro del tabulato dallo scaffale di output. E l’esultanza nel leggere il risultato atteso.
Ripercorriamo la storia dell’equazione di Leonardo, per proseguire con uno sguardo agli strumenti disponibili oggi per risolverla.
La sfida
Nel luglio del 1226, l’imperatore Federico II di Svevia volle incontrare il matematico Leonardo da Pisa, detto il Fibonacci, che aveva fama di grande matematico. Un imperatore illuminato, Federico II, appena due anni prima aveva istituito l’università di Napoli.
L’incontro avvenne a Pisa. Per apprezzare le competenze matematiche del Fibonacci, l’imperatore gli fece porre delle questioni dal suo filosofo di corte, il Maestro Giovanni Panormita. Una delle questioni riguardava la risoluzione dell’equazione di terzo grado: x3 + 2x2 + 10x = 20.
Naturalmente la domanda fu posta con la notazione matematica del tempo, del tutto priva di simboli:
Ut inveniretur quidam cubus numerus, qui cum suis duobus quadratis et decem radicibus in unum collectis essent viginti.
Non c’era solo un problema di notazione. Oggi un’equazione di questo tipo si scrive portando tutti i termini a sinistra del segno di uguale, accettando come normalità che alcuni coefficienti risultino negativi: x3 – 2x2 + 10x – 20 = 0.
All’epoca, invece, l’equazione consisteva nell’uguaglianza di due membri, ciascuno privo di termini negativi. Ad esempio l’equazione:
x3 – 2x2 + 10x – 20 = 0
sarebbe stata proposta con una frase in latino equivalente a:
x3 + 10x = 2x2 + 20.
Uno egli aspetti negativi di questa notazione, poi superato con l’introduzione della possibilità di termini a coefficiente negativo, era che ogni combinazione di termini positivi/negativi (o assenti) portava a un tipo di equazione differente, ciascuno con un approccio di risoluzione diverso.
L’equazione di Leonardo, nell’approccio del Fibonacci
La questione posta dal Panormita era stata pensata con cura. Con una diversa scelta dei coefficienti la questione si sarebbe potuta rivelare banale. Nell’esempio appena riportato, l’equazione ammette una sola soluzione reale, pari a 2.
La risposta del Fibonacci per forza di cose fu articolata:
- dimostrò innanzitutto che l’equazione ammetteva una sola soluzione (la consapevolezza di soluzioni espresse da numeri complessi era di là da venire);
- provò inoltre che la soluzione non era esprimibile come numero razionale, cioè con una frazione;
- da ultimo diede una soluzione approssimata: 1 + 22/60 + 7/602 + 42/603 + 33/604 + 4/605 + 40/606
L’approssimazione dà un valore di 1.3688081078532237…, che differisce dal valore corretto solo a partire dall’undicesima cifra decimale: 1.36880810782137…
Un simile grado di precisione costituiva un record assoluto in Europa, nessun altro matematico dell’epoca avrebbe potuto competere.
L’utilizzo della notazione in base 60 è ritenuto un indizio sul metodo seguito da Leonardo per fornire il risultato. Tale metodo, infatti, non fu rivelato dal Fibonacci, cosa normale in un periodo storico in cui la risoluzione di equazioni di grado superiore al 2 era un campo di ricerca aperto, e in cui un matematico si guadagnava da vivere risolvendo sfide.
Come si affronta oggi l’equazione di Leonardo
Poche righe di codice Python risolvono in un batter d’occhio la questione:
from sympy import symbols, Eq, solve, print_latex
x = symbols('x')
eq1 = Eq(x**3 + 2*x**2 + 10*x, 20)
sol = solve((eq1), (x))
for s in sol:
print ('radice: {}'.format(s))
print ('valore: {}'.format(s.evalf()))
La magia è fatta dalla libreria Python sympy, che consente il calcolo simbolico. Il codice non fa altro che importare da quella libreria le funzioni necessarie, scrivere l’equazione e chiedere di risolverla. Poi si passa a stampare l’espressione e il valore di ciascuna delle tre radici, che la funzione solve() restituisce in una lista di tre elementi.
Il tutto si esegue semplicemente, gratuitamente, da browser e senza installare nulla sul pc, tramite il sito di Google Colaboratory.
Come già sappiamo due radici sono espresse da numeri complessi. La radice reale viene restituita come:
radice: -26/(9*(352/27 + 2*sqrt(3930)/9)**(1/3)) -
2/3 + (352/27 + 2*sqrt(3930)/9)**(1/3)
valore: 1.36880810782137
L’espressione della radice è poco leggibile. Niente paura, basta aggiungere una riga di codice, per stampare la radice reale in formato LaTex:
print_latex(sol[2])
L’output è:
- \frac{26}{9 \sqrt[3]{\frac{352}{27} + \frac{2 \sqrt{3930}}{9}}} -
\frac{2}{3} + \sqrt[3]{\frac{352}{27} + \frac{2 \sqrt{3930}}{9}}
No, non è come sembra, non abbiamo complicato a piacere la situazione. Siamo effettivamente a un passo dal visualizzare una forma compatta della radice. Basta infatti inserire in Google Colab una cella di testo in cui copiare questa stringa racchiudendola tra due simboli ‘$’ e voilà, la magia è completa: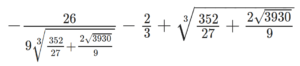
Sicuramente c’è un modo per fare tutto via codice Python, ma la pigrizia mi ha guidato a questo finale artigianale.
L’equazione di Leonardo, con l’informatica del 1973
All’epoca un elaboratore poteva dare una mano validissima, ma solo eseguendo calcoli numerici con precisione e velocemente. Bastava pensare un algoritmo, tradurlo in codice (Fortran nel mio caso) e sottoporlo all’elaboratore.
Si parte dalla funzione y = x3 + 2x2 + 10x – 20, che si azzera quando x assume il valore di una delle radici reali dell’espressione a destra della virgola. Poiché la funzione è continua, cioè non fa salti, nell’attraversare l’asse delle x sarà positiva da un lato e negativa dall’altro. Google ci dà una mano a visualizzare (oggi, mentre allora si andava solo di carta e matita):
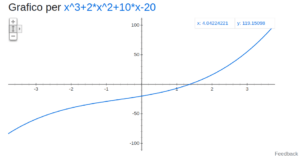
Inciso: zoommando gli assi, si può arrivare a leggere un valore grossolanamente preciso della radice. Ma questa è proprio da pigri all’ennesima potenza.
Bene, una volta stabilito che per x = 0 la funzione è negativa e per x = 2 è invece positiva, la continuità ci garantisce che esiste almeno un valore tra 0 e 2 in cui la funzione si annulla.
Si provi allora a calcolare il valore della funzione nel punto a metà strada tra 0 e 2, cioè per x = 1. La funzione in quel punto vale 13 + 2 ×12 + 10 × 1 – 20 = -7. Si può allora dimezzare l’intervallo di ricerca, scegliendo la parte a destra compresa tra 1 e 2.
Passo dopo passo, dimezzando l’intervallo ad ogni passo, si può arrivare alla precisione consentita dal linguaggio a disposizione.
Proviamo a eguagliare Leonardo
Del codice in Fortran ho già detto che non ricordo nulla, riscritto in Python dovrebbe essere più o meno così:
def fibo(x):
return x**3 + 2*x**2 + 10*x -20
#
x_min, x_max = 0, 2
f_min, f_max = fibo(x_min), fibo(x_max)
if f_min * f_max < 0:
max_err = 0.0000000001
step, max_step = 0, 100
err = x_max - x_min
#
while err > max_err and step < max_step:
x = (x_min + x_max)/2
f_x = fibo(x)
z = f_x * f_min
if z < 0:
x_max, f_max = x, f_x
elif z > 0:
x_min, f_min = x, f_x
else:
print ('{} soluzione esatta!'.format(x))
break
err = x_max - x_min
step += 1
print ('in {} passi, valore approssimato della radice: {}'.format(step,x))
elif f_min * f_max == 0:
print ('uno tra {} e {} è la soluzione esatta!'.format(x_min,x_max))
else:
print ('nell\'intervallo ({},{}) '.format(x_min,x_max) + \
'potrebbero non esserci radici reali, scegli un altro intervallo')
Rispetto all’originale del 1973 credo di aver inserito un pochino di generalità in più: lo stesso codice si adatta ad altre equazioni, anche con andamento discendente. Ho anche inserito un controllo del numero massimo di passi da eseguire. Ricordo che imparai a inserire questo tipo di controllo quando un errore di programmazione mi fece stampare un tabulato di un centinaio di pagine (con conseguente veemente reprimenda da parte dell’operatore IT del centro di calcolo).
L’output:
in 35 passi, valore approssimato della radice: 1.368808107858058
Leonardo da Pisa, detto il Fibonacci, ha tutta la mia ammirazione!
Immagini create dall’Intelligenza artificiale (AI)
L’immagine di apertura è stata creata combinando due delle immagini create dall’algoritmo di Intelligenza Artificiale del sito Dall-e-2.
Grazie a una rapidissima evoluzione di queste tecniche, esistono diverse proposte in questo campo. Dall-e-2 (erede di Dall-e) è probabilmente, al momento, la proposta migliore. Segnalo anche il sito Craiyon.com, che si autodefinisce Dall-e Mini.
Ho selezionato le due immagini dal gruppo di 4 generate in base al testo:
Medieval mathematician solves a complicated third degree equation, thanks to an innovative algorithm.
È possibile fornire all’algoritmo anche un’immagine di partenza, di cui saranno quindi generate variazioni a tema.
Siamo alla fine dell’arte come la conosciamo oggi? Non sono un esperto, quindi non mi esprimo. Penso però che questi strumenti, in mano a un creativo (cosa che non sono), possano aprire a nuove forme d’arte.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it




