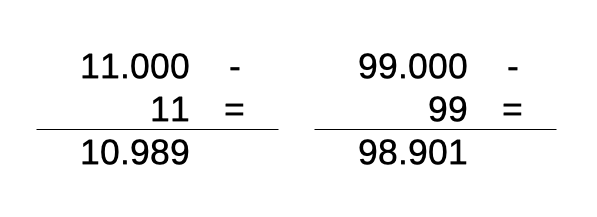
Il numero 21978 ha una particolare proprietà: se moltiplicato per 4 dà come risultato 87912, cioè le sue stesse cifre, ma in ordine inverso.
A propormi questa curiosità è stata, qualche settimana fa, l’email periodica di Quora, che mi ha rimandato a questo articolo. Pura matematica ricreativa, certamente però stimola qualche domanda: ci sono altri numeri con questa proprietà? Con quali algoritmi cercarli?
Uno sguardo alla struttura di 21978
La prima osservazione che viene da fare è che 21978 può essere derivato per sottrazione di 22 dal numero 22.000. Questo non spiega perché il suo prodotto per 4 dia come risultato il suo palindromo, ma fornisce un indizio su come generare altri palintiples imparentati a 21978.
Guardando infatti alle due sottrazioni a destra nell’immagine, si vede che il ruolo del 9 è di puro passacarte nella trasmissione del riporto verso sinistra, quindi viene il sospetto che possa essere eliminato, oppure che possano essere aggiunti altri 9, conservando la proprietà della simmetria tra moltiplicando e risultato.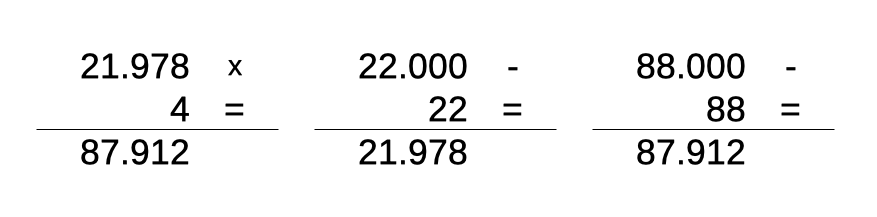
E, infatti, eliminando il 9, si arriva al più semplice di questa famiglia di palintiples, il numero 2178:
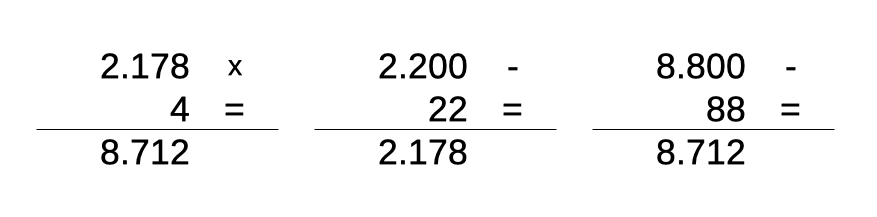Una cosa analoga avviene aggiungendo un 9, accanto a quello già esistente:
Si può quindi concludere che esiste un famiglia di infiniti numeri che, moltiplicati per 4, danno il palindromo del numero stesso:
2178, 21978, 219978, 2199978, … »»» 8712, 87912, 879912, 8799912, …
È bene osservare che questa proprietà vale strettamente nella base di numerazione che utilizziamo abitualmente, cioè la base 10. In una base diversa, binaria ad esempio, oppure in quella base 12 che qualcuno vorrebbe adottassimo, cambierebbe radicalmente la rappresentazione dei nostri palintiples e verrebbe a cadere la simmetria tra moltiplicando e risultato.
Per chi fosse interessato a giocare con diverse basi numeriche, rimando all’articolo “Numeri palindromi e altre noiosità“.
Alla ricerca di un altro Palintiple
Esistono altri numeri con la stessa proprietà, e che non siamo derivabili da 2178?
Il metodo più semplice è quello di scrivere un semplice programma che esplori almeno il pezzetto iniziale dell’infinita vastità dei numeri naturali. L’algoritmo che viene in mente è abbastanza semplice:
- per ogni numero naturale compreso in un certo intervallo,
- si ricava il suo palindromo,
- e si verifica se il rapporto tra i due numeri è un intero esatto.
Vanno prese però due precauzioni: al passo 1 occorre evitare i numeri che terminano con la cifra 0, perché rovesciando le cifre lo zero si sposterebbe nella posizione più significativa; al passo 3 va evitato il caso in cui il numero coincida con il suo palindromo.
Tutto ciò si può realizzare con poche righe di Ruby:
# ricerca di interi positivi multipli o sottomultipli del loro palindromo
(101..999999).each do |i|
next if i%10 == 0
j = i.digits.join.to_i
if (i != j) and ((j%i == 0) or (i%j == 0)) then print i, "\t", j, "\n" end
end
Ruby fornisce dei metodi molto comodi per questo tipo di analisi:
- .digits fornisce un array con le cifre del numero a cui si applica, nell’ordine che serve a noi, dalla cifra meno significativa a quella più significativa;
- .join raggruppa gli elementi dell’array in una stringa;
- .to_i trasforma la stringa con caratteri numerici, nel numero corrispondente.
La seconda riga imposta l’intervallo numerico da esplorare, da 101 a 999.999, mentre la terza salta i numeri che terminano con 0 (multipli di 10).
La quinta riga, infine, stampa solo i numeri che soddisfano il criterio di ricerca: i numeri i e j, palindromo uno dell’altro, sono diversi tra loro e il loro rapporto è un numero intero.
Infine il carattere % è l’operatore dell’aritmetica modulare: i % 10 fornisce il resto della divisione di i per 10.
And the winner is …
Questo l’output del programma:
1089 9801 2178 8712 8712 2178 9801 1089 10989 98901 21978 87912 87912 21978 98901 10989 109989 989901 219978 879912 879912 219978 989901 109989
Si nota che la lista dei palintiples trovati è l’unione di due liste: quella già nota, basata sulla coppia 2178 / 8712 e una seconda lista, analoga alla prima, ma basata sulla coppia 1089 / 9801.
Uno sguardo alla nuova serie
Osservando la coppia 10989 e 98901, non sfugge la somiglianza con 21978 e 87912:
E, infatti, anche in questo caso il 9 al centro del numero fa passacarte per il passaggio del riporto nella sottrazione. Quindi, anche in questo caso, si può sia eliminare il 9 che aggiungerne a volontà:
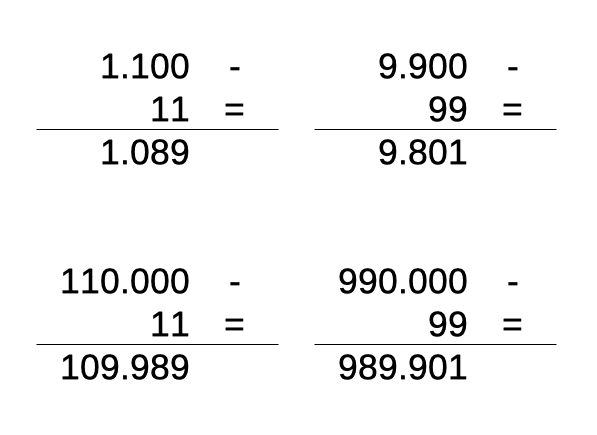Ma non basta ancora!
Sulla base delle due famiglie trovate, se ne possono costruire infinite altre con una semplice osservazione. Guardiamo cosa accade al numero 21782178, ottenuto ripetendo due volte di seguito le cifre di 2178:
È come se si fondessero per accostamento due repliche della stessa moltiplicazione. È evidente che questa operazione può essere ripetuta infinte volte, per ciascuna delle coppie base trovate (2178 / 8712, 21978 / 87912, 219978 / 879912, …, 1089 / 9801, 10989 / 98901, …).
E la simmetria si conserva anche accostando opportunamente palintiples diversi, della stessa famiglia:
In questo caso ho sistemato a panino un 10989 tra due 1089.
I palintiples nell’Enciclopedia online delle sequenze di interi (OEIS)
L’algoritmo di esplorazione utilizzato consente allo sguardo di andare appena più in là della semplice osservazione carta e matita. Non ha certo la pretesa di fornire una risposta esaustiva sull’esistenza dei palintiples: ci saranno altre famiglie di base, oltre le due trovate?
Una risposta si può trovare nell’Enciclopedia online delle sequenze di interi, l’OEIS. La sequenza che ci interessa è la sequenza A008919, che comincia così:
1089, 2178, 10989, 21978, 109989, 219978, 1099989, 2199978, 10891089, 10999989.
A prima vista sembra che tutti i numeri della sequenza mostrati nella pagina web siano riconducibili a quanto trovato con il semplice algoritmo utilizzato. Sarà così? Devo approfondire.
L’immagine di apertura dell’articolo è di Ulrike Leone da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
Articoli correlati:
