Algoritmi, che passione!

Una dei momenti più divertenti e appassionanti dell’attività informatica è la progettazione degli algoritmi: idearli, mettere giù i codici, provarli con i primi dati di test e scoprire che non funzionano come dovrebbero.
Ripensarne la logica, modificare il codice, riprovare con test via via più complessi, simulando le condizioni limite a cui la creatura dovrà far fronte. Ripetere, fino a quando non siano diventati abbastanza solidi da affrontare i dati reali.
Di tutti gli algoritmi realizzati (in alcuni casi anche ideati), sono affezionato in particolar modo a due, che misi a punto nel tempo libero a fine anni ’70, quando ero progettista hardware, fresco di laurea e appena assunto alla Olivetti di Ivrea.
Il primo era legato alla selezione equiprobabile di un elemento in un gruppo di campioni, l’altro era relativo all’ordinamento di valori numerici, e si merita un post a parte.

---

Algoritmi, il gioco si fa elettronico

A fine anni ’70 comparvero i primi aggeggi elettronici per il gioco degli scacchi, capaci di tener testa a un giocatore medio-basso come me.
La comparsa dei primi rivoluzionari microprocessori, come lo Zilog z80 e il 6502 della MOS Technology, rendeva da un lato fattibili i primi computer personali (Sinclair ZX Spectrum per il primo, il Commodore VIC 20 per il secondo), dall’altro consentiva di concentrare in poco spazio, e a un costo ragionevole, la capacità di calcolo per applicazioni specializzate, come appunto l’automazione del gioco degli scacchi.

Rimasi intrigato da un articolo di Martin Gardner comparso nella sua rubrica pubblicata su “le Scienze”, con la descrizione dell’algoritmo min-max alla base di quella automazione, e, avendo a disposizione nei ritagli di tempo libero il laboratorio di lavoro di Mamma Olivetti, decisi di provare a realizzare qualcosa sul tema.

Lungi dal cimentarmi sugli scacchi, scelsi un gioco più semplice, popolare e divertente, non ancora investito dall’ondata informatica, il Reversi.

Gli algoritmi e il gioco del Reversi

La solita Wikipedia spiega molto bene le regole e le strategie di base per giocare al Reversi.
In sintesi estrema:

• si gioca su una tavola di 8×8 caselle, tutte colorate uniformemente di verde;
• i due giocatori hanno a disposizione 64 pedine bianche da un lato e nere dall’altro;
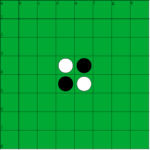
• inizialmente sono già occupate le 4 caselle centrali, come si vede nella prima figura che segue;
• alternativamente, a partire dal nero, ciascun giocatore deposita una pedina in una casella vuota, con il proprio colore all’insù, purché, tra la pedina che viene depositata e un’altra dello stesso colore, siano racchiuse una o più pedine dell’altro colore in una fila orizzontale, verticale o diagonale; se ciò non è possibile, il giocatore salta il turno;
• tutte le pedine così racchiuse, in tutte le direzioni possibili, vengono capovolte, conquistate da chi effettua la mossa;
• il gioco termina quando tutte le caselle sono occupate, oppure quando nessuno dei due giocatori può più muovere;
• a quel punto vince chi ha più pedine.

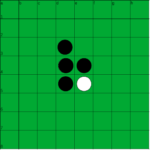
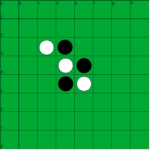
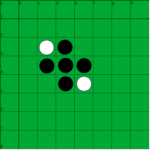
Qui di seguito le prime mosse di una partita di Reversi.

L’algoritmo min-max

L’algoritmo min-max si propone di scegliere la mossa migliore per un giocatore virtuale, data una certa situazione di gioco.
Rimandando ancora una volta a Wikipedia per un’esposizione più completa dell’algoritmo, quella che segue è una veloce spiegazione.

A partire dalla situazione di gioco attuale, l’algoritmo prevede di analizzare una per una, tutte le mosse possibili per il giocatore virtuale che deve muovere. Per ciascuna mossa, viene quindi analizzata ogni possibile risposta dell’altro giocatore e, per ciascuna di queste, viene analizzata ogni possibile contro-risposta del primo giocatore. E così via, per il numero di livelli desiderato.

Supponiamo, per semplicità, che si analizzino i primi tre livelli.
Dopo mossa e risposta, l’algoritmo genera quindi tutte le situazioni generate dalle possibili terze mosse. A ciascuna di queste situazioni viene attribuito un punteggio, in base a una valutazione posizionale (quanti pezzi ha ciascun giocatore, come sono disposti, il numero di mosse possibili da quella posizione e così via).

Poiché la terza mossa è del giocatore che muove, è ovvio che questi sceglierebbe come terza mossa quella che massimizza il punteggio della situazione di arrivo.

Al livello precedente (che toccherebbe all’altro giocatore), questi sceglierebbe ovviamente la mossa a cui corrisponde il minimo valore delle situazioni successive (la situazione meno-peggio per lui). E al primo livello, il giocatore virtuale sceglierebbe il massimo valore fra questi minimi.

Dall’alternanza di minimi e massimi deriva il nome dell’algoritmo. L’intelligenza dell’algoritmo sta tutta nei criteri utilizzati nella valutazione posizionale.

Algoritmi, la realizzazione pratica hardware

La componente hardware era la parte meno complessa per me, visto che il mio lavoro era proprio il progetto hardware.
Processore z80 con clock a 2.5 MHz, 8 chip di memoria DRAM da 16 kbit, per realizzare 16 kByte di memoria. Programma contenuto in una EPROM da 32 kByte, pochi componenti di contorno, il tutto in una scatoletta ricavata saldando ritagli di scarto di circuito stampato.

Il cervello elettronico era comunque di tutto rispetto, in linea con la tecnologia disponibile al momento. Quello che lasciava a desiderare era l’interazione umana, che passava per un semplice display a matrice di led e a due tasti: reset e scegli (tra le opzioni che scorrevano sull’unica riga del display).

Il software

Il programma sviluppato consentiva di gestire partite di Reversi tra due giocatori, che potevano essere sia umani che virtuali. Escluso il caso terribilmente inefficiente di umano-vs-umano, era possibile gestire quindi partite umano-vs-virtuale e virtuale-vs-virtuale.

Per il giocatore virtuale era possibile scegliere il numero di livelli su cui far lavorare l’algoritmo min-max (3 livelli era il massimo accettabile, a patto di non avere fretta), e una tra diverse valutazioni posizionali.
Era quindi possibile mettere a confronto differenti criteri di valutazione, in modo da individuare il più furbo ed eventualmente mettere a punto migliorie.

I risultati

Per assegnare una valutazione oggettiva a ciascun criterio di valutazione, avevo predisposto un giocatore virtuale di riferimento, che sceglieva a caso tra le mosse possibili. Dopo 100 partite tra il giocatore virtuale sotto esame e quello di riferimento, il numero di partite vinte dal primo forniva una semplice e significativa indicazione della sua efficacia.

Un indice di 50 significava che l’algoritmo non aveva di fatto alcuna intelligenza, mentre un algoritmo molto efficiente avrebbe raggiunto il massimo valore, 100.
Non superai mai 85. Cioè, il miglior criterio di valutazione posizionale che misi a punto, perdeva comunque il 15% delle volte contro un giocatore che non applicava nessun criterio, se non il caso.

Deludente, ma mi divertii un sacco e imparai molte cose, gestendo in proprio tutti gli aspetti di un progetto, cosa che nel lavoro reale non era ipotizzabile per un quasi neo-assunto.

L’algoritmo di selezione equiprobabile

Una premessa: mi sono laureato al Politecnico di Napoli, specializzazione Telecomunicazioni. La formazione era eccellente per quanto riguarda il progetto hardware, mentre, in quel lontano 1973-1976, il progetto software era meno sviluppato che in altre realtà universitarie.
Per esemplificare, avevo studiato in dettaglio gli algoritmi per la sintesi circuitale di moltiplicazioni tra numeri, ma non sapevo nulla della gestione delle code. Le mie soluzioni algoritmiche quindi favorivano forzatamente la semplicità di realizzazione a scapito della purezza informatica.

Nel realizzare il mio giocatore di riferimento, la soluzione canonica avrebbe previsto:

• sistemare in una lista le mosse possibili, man mano che venivano trovate;
• contarne il numero (N);
• scegliere un numero a caso con equiprobabilità tra 1 e N.

Il primo punto mi sembrava complicato (non avevo mai gestito una lista). Mi chiesi quindi se non fosse possibile scartare una mossa ogni volta che avessi trovato la successiva, pur assegnando a ognuna delle possibili mosse la stessa probabilità di successo. Il vantaggio sarebbe stato quello di non avere una lista di mosse tra cui scegliere alla fine, ma effettuare una serie di semplici scelte binarie.

Algoritmi, i pesi della scelta

Supponiamo che le mosse possibili siano solo 4: S₁, S₂, S₃, S₄, e che vengano trovate in quest’ordine. Ognuna deve essere scelta con probabilità 1/4 = 25%.

Il mio algoritmo deve quindi inizialmente scegliere tra S₁ed S₂, poi tra la superstite di questa scelta e S₃, infine tra la nuova superstite e S₄.
Se a ogni scelta ho una probabilità uguale per le due contendenti (50% e 50%), evidentemente la favorita è S₄, la più sfigata è S₁. Occorre quindi modificare la distribuzione di probabilità a ogni giro.

Al primo confronto è giusto assegnare un’uguale probabilità alle due scelte (1/2 e 1/2). Invece al secondo occorre tener conto che la superstite del primo giro ha già effettuato un confronto, quindi deve avere probabilità doppia (2/3) rispetto alla terza contendente (1/3).
Analogamente, al terzo confronto la superstite, che ha già effettuato due confronti (effettivi o equivalenti), deve avere probabilità tripla (3/4) rispetto alla nuova contendente (1/4).

Generalizzando, l’algoritmo può quindi essere sintetizzato così:

• comincio a selezionare la prima mossa possibile trovata, S₁;
• quando trovo l’ennesima mossa possibile S_N, seleziono questa con probabilità 1/N e, quindi, conservo la superstite con probabilità (N-1)/N.

Algoritmi, una verifica con Ruby

Poche righe di programma in linguaggio Ruby consentono di verificare se l’algoritmo funziona.

n_campioni = 4
n_cicli = 1000 * n_campioni
conta = Hash.new(0)
#
(1..n_cicli).each do |ciclo|
	best = 1
	(2..n_campioni).each do |campione|
		x = Random.new.rand(1..campione)
		if x == 1 then best = campione end
	end
	conta[best] += 1
end
print conta.sort.to_h

Il programma effettua un numero di cicli di simulazione pari a 1.000 volte il numero di campioni. Questo rende semplice la verifica visiva della bontà dell’algoritmo: idealmente ogni campione dovrebbe essere scelto 1.000 volte.

Questo il risultato di una esecuzione del programma:

{1=>1023, 2=>1035, 3=>978, 4=>964}

Cosa accade con più campioni, ad esempio con 20 campioni?

{1=>1022, 2=>1037, 3=>1016, 4=>1000, 5=>992, 6=>947, 7=>961, 8=>999,
9=>1060, 10=>1039, 11=>947, 12=>979, 13=>973, 14=>1036, 15=>1011,
16=>1038, 17=>1000, 18=>982, 19=>960, 20=>1001}

---

Ho scoperto come gestire liste e code solo successivamente. Per fortuna, perché quella iniziale ignoranza mi ha regalato l’occasione per una sana e impagabile ginnastica mentale. Sarebbe da considerare una sorta di pensiero laterale, se non fosse per il fatto che in effetti fu la pigrizia a farmi evitare la via canonica.

La foto di apertura del post è di TeroVesalainen da Pixabay