Quest’anno la Pasqua si celebrerà il 17 aprile. Sarà domenica, perché la Pasqua cade sempre di domenica, mentre giorno e mese ballano da un anno all’altro: la Pasqua 2021 è capitata il 4 aprile, l’anno prossimo invece festeggeremo il 9 aprile.
Ma la Pasqua può cadere anche in marzo, come è avvenuto l’ultima volta il 27 marzo del 2016, e ricapiterà nel 2024 (31 marzo).
Qual è allora l’algoritmo che assegna la data di Pasqua?
La regola che decide la data è complicata da decifrare ed è basata sul ciclo lunare. Talmente complicata, almeno per me, da farmi desistere nei mei ripetuti tentativi di venirne a capo.
Per fortuna nel 1800 il grande matematico Carl Friedrich Gauss tradusse il procedimento in un algoritmo matematico molto semplice da eseguire. Ancora più semplice è far ricorso a una funzione built-in della libreria dateutil di Python.
Vediamo in dettaglio le due procedure, insieme a qualche curiosità statistica.
La data di Pasqua e il ciclo lunare
Wikipedia racconta:
La Pasqua ebraica è celebrata al tramonto del giorno 14 del mese di Nisan del calendario ebraico, come prescrive la Bibbia. Ogni mese di tale calendario ha inizio con la luna nuova e il quindicesimo giorno coincide con il plenilunio. […] Il 15 del mese di Nisan dovrebbe corrispondere sempre al primo plenilunio successivo all’equinozio di primavera (20 marzo).
Poco più avanti, Wikipedia descrive invece come la cristianità ha fissato la data della Pasqua:
Il principio-regola che fissa la data della Pasqua cristiana fu stabilito a seguito del Concilio di Nicea (325): la Pasqua cade la domenica successiva alla prima luna piena di primavera (all’epoca dei primi computi l’equinozio cadeva il 21 marzo, che pertanto divenne la data di riferimento).
Peccato che il calendario cristiano non sia basato sul ciclo lunare. E per non farci mancare nulla, il calendario attuale (gregoriano) è in funzione solo dal 1582, quando sostituì il precedente calendario giuliano.
Il calendario giuliano
Per diversi secoli i Romani hanno utilizzato un calendario che richiedeva una regolazione manuale, per così dire, per far corrispondere la durata media dell’anno calcolato con quella dell’anno solare. Basato su dieci mesi, venivano poi aggiunti i giorni necessari a quadrare i conti, anno per anno.
La prima razionalizzazione del calendario avvenne con il calendario Giuliano, elaborato dall’astronomo egizio Sosigene di Alessandria e tradotto in legge da Giulio Cesare, nel 46 a.C. Il calendario Giuliano era basato sulle stagioni e introduceva il concetto di anno bisestile, per tener conto della durata effettiva di un anno terrestre, poco più lunga di 365 giorni esatti.
La regola che fissava le annualità bisestili (una ogni 4 anni) non venne però inizialmente applicata correttamente, accumulando un po’ di bisestili in più.
Toccò quindi all’imperatore Ottaviano Augusto rimettere a posto le cose, nell’8 d.C., dopo di che il calendario tenne abbastanza bene per diversi secoli, anche se la durata media dell’anno era lievemente maggiore del dovuto.
Il calendario Gregoriano
Si arriva così al 1582. Lo spostamento che si è accumulato è sensibile, 10 giorni. Il Papa Gregorio XIII crea un gruppo di lavoro, tra ecclesiastici esperti chi in matematica, chi in astronomia, ma c’erano anche teologi ed esperti delle leggi della Chiesa. La soluzione che viene scelta è quella attuale, che non considera bisestili gli anni che terminano un centenario (1700, 1800, …), purché non siano multipli di 400 (e quindi 1600 e 2000 rimangono bisestili).
Per recuperare i giorni di ritardo accumulato, si decide che il giorno successivo al 4 ottobre 1582 sia il 15 ottobre, azzerando in un colpo solo lo scostamento.
La riforma viene accolta subito dalle nazioni cattoliche, mentre le altre rifiutano la riforma e solo successivamente si allineeranno.
La Svezia, ad esempio, lo farà nel 1699, scegliendo però di assorbire lo scostamento in modo graduale, cancellando i prossimi 10 anni bisestili. Purtroppo però, eliminato il primo, dimenticano di eliminare i successivi 9. Di fatto ritornano al calendario giuliano fino al 1753, data in cui recupereranno in un colpo solo lo scostamento.
La Cina passerà al calendario gregoriano nel 1912, la Russia nel 1917, grazie a Lenin.
La Rivoluzione di Ottobre è appena avvenuta, ma in novembre, per colpa del calendario giuliano. La Chiesa Ortodossa rimarrà fedele però al calendario giuliano e questo spiega perché le festività religiose ortodosse siano spostate in avanti rispetto a quelle cattoliche.
La data di Pasqua: algoritmo di Gauss
Si fa prima a scrivere il codice che a descriverlo a parole:
# Calcolo della data di Pasqua con il procedimento di Gauss
# I valori e sono specifici per la fascia di anni che va dal 1900 al 2099
x,y = 24,5
for year in range(1900,2100):
a = year % 19
b = year % 4
c = year % 7
d = (19 * a + x) % 30
e = (2*b +4*c + 6*d + y) % 7
if d + e <= 9: day,month = 22 + d + e, 3 elif d + e > 9:
day, month = 22 + d + e - 31, 4
# eventuale correzione
if d + e == 35:
day, month = 19, 4
if d + e == 34 and d == 28 and a > 10:
day, month = 18, 4
print (year, ';', str(day)+'/'+str(month))
Piccola guida:
- i valori x e y variano di secolo in secolo, quelli indicati sono quelli corretti nella fascia dal 1900 al 2099;
- l’operazione year % 19 indica il resto della divisione del valore year per 19; analogamente per gli altri utilizzi dell’operatore %;
- l’istruzione: day, month = 19, 4 assegna simultaneamente il valore 19 a day e il valore 4 a month.
Il programma genera le date della Pasqua per gli anni dal 1900 al 2099, nel formato:
2021 ; 4/4
2022 ; 17/4
2023 ; 9/4
2024 ; 31/3
2025 ; 20/4
2026 ; 5/4
2027 ; 28/3
Importando l’output in un foglio di calcolo, le date verranno lette come appartenenti tutte all’anno corrente (il 2022), il che semplifica l’estrazione di statistiche.
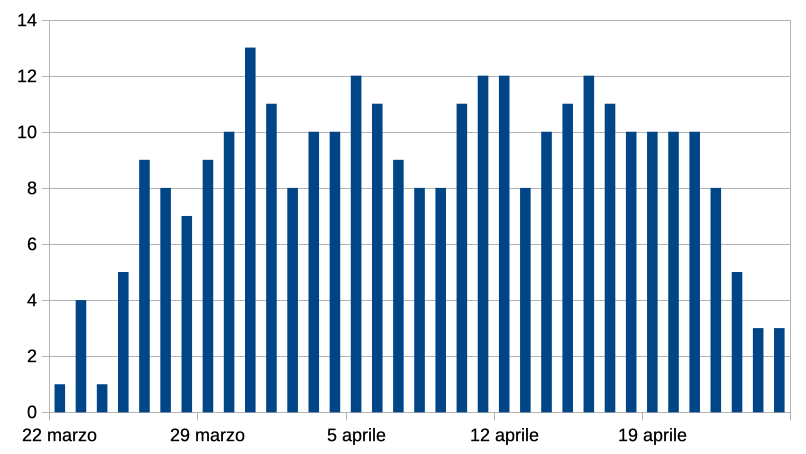
La distribuzione delle date è riportata nel grafico che segue:
Qualche osservazione:
- la Pasqua più anticipata possibile si ha quando il primo plenilunio di primavera capita un sabato 21 marzo, in questo caso il giorno dopo, 22 marzo, è Pasqua; è capitato nel 1818;
- la Pasqua più in ritardo si ha con un plenilunio il 20 marzo, di sabato; il successivo seguirà 29 giorni dopo, domenica 18 aprile e quindi Pasqua capiterà ancora una settimana dopo, il 25 aprile; è capitato nel 1943, succederà di nuovo nel 2038;
- dal grafico sembra esserci una lieve preferenza per il 31 marzo.
Rimane da vedere se ho realizzato correttamente l’algoritmo.
La data di Pasqua: la funzione Python “dateutil.easter”
from dateutil.easter import *
print ('Anno;formato US; gg/mmmm; gg/mm/aaaa')
for year in range(1583,1583+5000):
print (year, ';', easter(year), end=';')
en_date = str(easter(year))
it_date = en_date[8:10] + '/' + en_date[5:7]
it_date_full = it_date + '/' + str(year)
print(it_date,';',it_date_full)
Confrontando i risultati dei due programmi, si verifica che le ricorrenze della Pasqua nel tratto comune sono identiche, benedicendo così la mia realizzazione dell’algoritmo di Gauss (evviva!).
La distribuzione delle date nel periodo di 5000 anni analizzato è come segue:
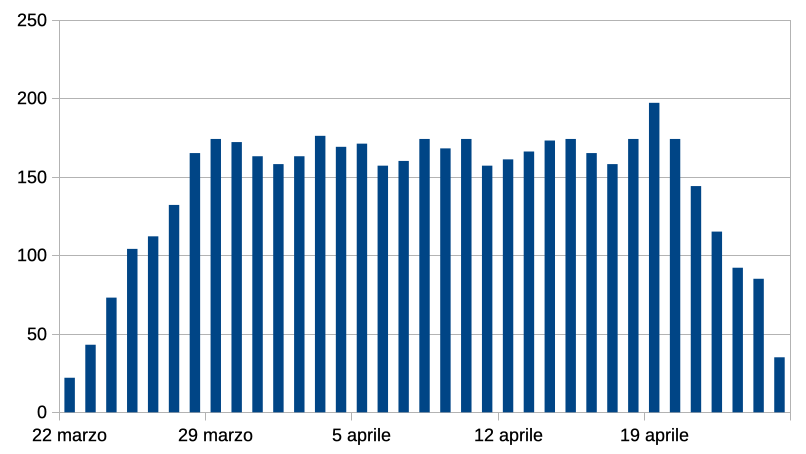Nel periodo più lungo la preferenza si sposta all’altro estremo delle possibili date, al 20 aprile. Si confermano 22 marzo e 25 aprile come date estreme.
Il codice Python riportato è stato eseguito su Google Colaboratory, il Jupyter Notebook reso disponibile gratuitamente da Google. Se ne è scritto qui.
I fogli di calcolo possono essere scaricati, invece, da qui, in formato LibreOffice ed Excel. Attenzione: nel formato excel le date anteriori al 1900 vengono visualizzate come errori.
Una descrizione decisamente completa della determinazione della data di Pasqua si trova su Matematicamente.it.
Immagine di apertura di Andreas Lischka da Pixabay.
Articoli correlati:
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
