Repunit, dall’inglese Repeated unit, è un numero formato solo dalla cifra 1, ripetuta quante volte si vuole. Quindi: 1, 11, 111, 1111, … sono tutti Repunit.
Poiché la matematica esige sintesi verbale, utilizzando simboli parlanti, un repunit con n cifre si indicherà con Rn.
Implicitamente mi sono riferito alla rappresentazione dei numeri in base 10, quella che utilizziamo comunemente per contare. Ma la definizione si applica anche ad altre basi di numerazione, ad esempio quella binaria: 111 in base 2 equivale a 7 in base 10. Ogni base merita una discussione a sé, qui ci limiteremo alla base 10.
La matematica pone domande
Tipiche domande da ricreazione matematica: ci sono quadrati perfetti tra i repunit? O meglio, più in generale, può un repunit essere una potenza di un numero intero? Ci sono numeri primi tra i repunit, oltre a 11?
Porre una domanda, nel campo della matematica, può essere molto semplice, ne abbiamo appena viste alcune. Rispondere può essere complicato a piacere.
Può un repunit essere un quadrato perfetto?
La risposta a questa domanda si trova con un ragionamento abbastanza semplice.
Se si esclude R1 (cioè 1), dividendo Rn per 4 si ha resto 3. Per convincersene, basta isolare le ultime due cifre e, poi, dividere per 4. Esempio: dividendo per 4 il repunit R5 = 11111 = 11100 + 11, il primo termine, multiplo di 100, dà contributo nullo al resto, che è quindi determinato dal secondo termine, 11. E il resto a 4 di 11 è pari a 3.
Ora, un qualunque numero dispari elevato al quadrato e diviso per 4 dà resto 1. Basta osservare che:
(2n +1)2 = 4n2 + 4n + 1
Quindi nessun repunit può essere il quadrato di un numero intero.
Questo semplice ragionamento esclude tutte le potenze pari. Infatti una sesta potenza, ad esempio, sarebbe il quadrato di una terza potenza, quindi anch’essa pur sempre un quadrato.
E per le potenze dispari?
Qui il discorso si fa più complicato. Una dimostrazione completa del fatto che un repunit non può essere la potenza di un numero intero si deve ai matematici francesi Yann Bugeaud e Maurice Mignotte, che nel 1999 hanno pubblicato diversi risultati sulle equazioni diofantee, tra cui appunto la non esistenza di repunit potenze di un numero intero:
We announce several new theorems on the Diophantine equation (xn−1)/(x−1)=yq, which include the fact that any integer greater than 2 and with all digits equal to 1 in base ten cannot be a pure power.
Cosa c’entrano le equazioni diofantee?
Basta osservare che Rn = 111…1 = 999…99/9 = (10n−1)/(10−1), e si arriva all’equazione citata appena sopra.
Per un altro articolo sulle equazioni diofantee, vedi Noci di cocco e marinai: l’indovinello di B. A. Williams, sempre su Inchiostro Virtuale.
Quanti repunit primi esistono?
Qui la faccenda si fa complicata, intrecciandosi al problema ad oggi insoluto della legge di distribuzione dei numeri primi.
Si congettura che esistano infiniti repunit che siano numeri primi, intanto perché non c’è prova del contrario, e poi perché esplorando la sequenza degli Rn, ogni tanto si inciampa in un numero primo.
Risultano infatti primi: R2(=11), R19, R23, R317.
Sono abbastanza rari i repunit primi e, in mancanza di altri criteri, occorre fattorizzare, cioè scomporre in fattori primi, ciascun candidato.
Per fortuna si può effettuare una buona scrematura iniziale. Si trova infatti che, perché Rn sia primo, anche n deve essere primo. Questo risultato è di quelli a cui si arriva con un semplice ragionamento.
Prendiamo in esame, ad esempio, R12, e ricorriamo a questa rappresentazione:
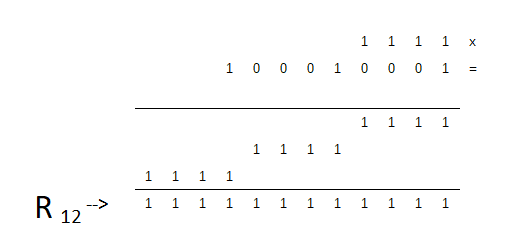Quindi R12 è divisibile per R4 e, ricorrendo a uno schema analogo, per R3. Divertente notare come l’altro fattore della scomposizione sia composto solo da 0 e 1.
In generale, Rn sarà divisibile per ogni fattore di n. Perché Rn sia primo, quindi, occorre che n sia primo.
Questa osservazione riduce sensibilmente il numero di repunit da esaminare e, inoltre, sono stati messi a punto altri criteri che restringono la ricerca. Rimane il fatto che ogni cifra che si aggiunge rende più lungo il lavoro di fattorizzazione.
Lo stato attuale della ricerca dei repunit primi
La pagina dedicata ai repunit su Mathworld.wolfram.com riporta lo stato attuale della ricerca sul tema: sono primi verificati gli Rn con n = 2, 19, 23, 317 e 1031, mentre sono sotto indagine gli Rn con n = 49081, 86453, 109297 e 270343.
La sezione di matematica del sito italiano Elektrosoft.it riporta lo stato del progetto di ricerca dei repunit primi, oltre ad alcune altre curiosità matematiche.
L’impatto del calcolatore elettronico sulla matematica
La storia della ricerca di repunit primi è uno dei tanti esempi dell’accelerazione consentita dal calcolo elettronico.
L’interesse sui repunit era nato nel diciannovesimo secolo, con la dimostrazione del fatto che, per ogni primo p maggiore di 5, il periodo dell’espansione decimale di 1/p è uguale alla lunghezza del più piccolo numero della forma 11…1, divisibile per p.
Esempio: 7 è primo, 1⁄p = 0,142857 142857 14…
La parte frazionaria è costituita dalla ripetizione della sequenza di 6 cifre: 142857. Se fattorizziamo i primi repunit:
R2 = 11 (primo)
R3 = 111 = 3 × 37
R4 = 1111 = 11 × 101
R5 = 11111 = 41 × 271
R6 = 111111 = 3 × 7 × 11 × 13 × 37
notiamo che il più piccolo repunit divisibile per 7 è proprio R6.
Da qui era nato lo sforzo per fattorizzare i numeri della forma 11…1, culminati nella scoperta che R19 è primo, da parte del matematico Oscar Hoppe nel 1916. Qualche anno dopo, nel 1929, Lehmer and Kraitchik dimostrarono che il primo successivo è R23.
Il primo successivo, come abbiamo visto, è R317, assolutamente fuori dalla portata di un calcolatore umano. E infatti per scoprirlo occorre attendere il 1960, con i primi calcolatori elettronici con una potenza sufficiente ad affrontare il problema.
I numeri di Mersenne
Lo stesso destino è stato vissuto dalla ricerca di primi ben più famosa dei numeri di Mersenne, quelli della forma 2n – 1, e indicati con Mn.
Nel 1876 il matematico francese Lucas trova che M127 = 2127 – 1 (numero di 39 cifre) è primo. Per trovare il successivo, M521, numero di 157 cifre, occorre attendere il 1952 e, naturalmente, un calcolatore elettronico: lo SWAC.
Dotato di 2300 valvole termoioniche, con una memoria di 256 parole, sapeva fare solo somme, sottrazioni, moltiplicazioni, comparazioni. Eppure era già incomparabilmente più veloce (e affidabile) del calcolo umano.
Il 1952 è il mio anno di nascita e, proprio nel 1952, il matematico statunitense Raphael M. Robinson fa compiere un balzo in avanti alla ricerca dei primi di Mersenne.
Comincia il 30 gennaio, con M521 e M607. Prosegue il 25 giugno con M1279 (due giorni dopo nasco io). Poi in ottobre, il 7 e il 9, rispettivamente M2.203 e M2.281. Il successivo, M2.281, arriverà cinque anni più tardi, nel 1957.
Doveva esserci qualcosa nell’aria, in quel lontano 1952.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
Articoli correlati:
