Qualche settimana fa, ho visto girare su Facebook un giochino matematico legato al simbolo del fattoriale. Originato da un tweet, in Italia è stato rilanciato da Linkiesta.it e suona più o meno così:
Non ci crederai, ma 230 – 220 × 0,5 = 5!
L’assenza di parentesi induce a pensare che il tranello sia nell’ordine delle operazioni, invece sta nell’ultimo carattere, in quel punto esclamativo che ha la doppia valenza di operatore matematico (il fattoriale di 5, per l’appunto, uguale a 120) e un’espressione di sorpresa.
Chissà quanti hanno calcolato e ricalcolato, finché non sarà tornata a galla la reminiscenza liceale legata a quel punto esclamativo.
(Per rinfrescarsi la memoria sull’ordine corretto con cui effettuare le operazioni, si rimanda all’articolo sul PEMDAS).
Cos’è un fattoriale
Per esprimere in modo conciso il prodotto dei numeri interi positivi da 1 a n si utilizza la notazione n!. Quindi, ad esempio:
5! = 1 × 2 × 3 × 4 × 5 = 120
Il simbolo del fattoriale trova largo utilizzo nel calcolo combinatorio: in quanti modi diversi posso sistemare 4 persone in fila?
I modi diversi sono 4! .
Ipotizziamo che le 4 persone siano A, B, C e D. Tutte le possibili permutazioni con A primo della fila sono 6 = 1 × 2 × 3 = 3! :
A B C D A B D C A C B D A C D B A D B C A D C B
Tenendo conto che tutti e 4 possono essere in cima alla fila, le combinazioni saranno quindi 24 = 4 × 3! = 4!
Altro esempio: se si desidera calcolare la probabilità di azzeccare la combinazione del superenalotto, è bene prepararsi a una scorpacciata di fattoriali.
Colonia 1808, nasce il simbolo del fattoriale
C’è un anno preciso, il 1808, e un luogo di nascita preciso, la città tedesca di Colonia, dove vede la luce il trattato Éléments d’arithmétique universelle. Il padre ufficiale del fattoriale è il matematico (e medico) francese Christian Kramp. Lavora sul calcolo combinatorio e l’operazione fattoriale ricorre spesso nelle sue dimostrazioni:
Je me sers de la notation trés simple n! pour désigner le produit de nombres décroissans depuis n jusqu’à l’unité, savoir n(n−1)(n−2)…3⋅2⋅1n(n−1)(n−2)…3⋅2⋅1. L’emploi continuel de l’analyse combinatoire que je fais dans la plupart de mes démonstrations, a rendu cette notation indispensable.
Non tutti sono dello stesso avviso: in realtà, un simbolo per il fattoriale, è già stato proposto ed è anche utilizzato. Consiste in un tratto a L che racchiude il numero n. Peccato che complichi non poco il lavoro degli stampatori, mentre il punto esclamativo va che è una bellezza.
Qualcuno prova a contrastare la novità. Il matematico-logico inglese Augustus De Morgan ci va giù deciso:
Among the worst barbarisms is that of introducing symbols which are quite new in mathematical, but perfectly understood in common, language. Writers have borrowed from the Germans the abbreviation n! … which gives their pages the appearance of expressing admiration that 2, 3, 4, etc., should be found in mathematical results.
L’accenno ai Germanici è dovuto al fatto che Kramp insegna a Colonia, città sotto il dominio francese dal 1794 al 1815.
Nonostante il rigore di De Morgan (che ha previsto con un paio di secoli di anticipo l’inganno del nostro indovinello iniziale), il punto esclamativo si diffonde rapidamente e si afferma assoluto vincitore.
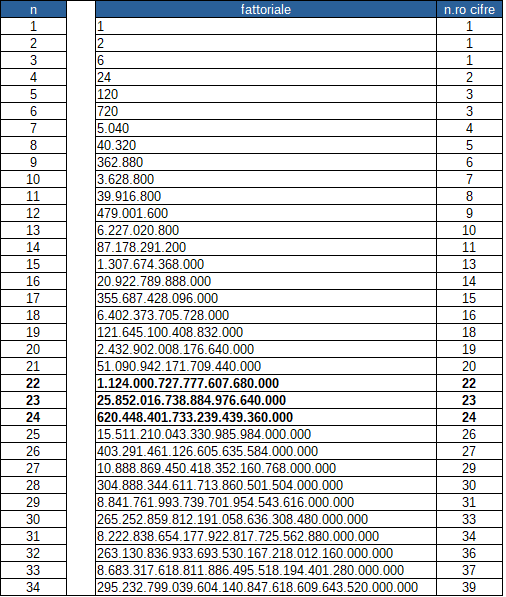
Numeri a crescita vertiginosa
Per sua stessa definizione, il fattoriale di un numero n è n volte il fattoriale del numero precedente; quindi, al crescere di n, il valore del relativo fattoriale cresce sempre più velocemente.
Un semplice file Libre Office Calc (o Excel) consente di calcolare le cifre dei fattoriali dei primi numeri naturali (il file è scaricabile da qui).
Evidenziati in grassetto i fattoriali di 22, 23 e 24, che hanno rispettivamente 22, 23 e 24 cifre. Da lì in avanti il ritmo di crescita del numero di cifre si accentua e nessun altro numero potrà avere questa proprietà.
Fun Facts sul fattoriale
1. Si potrebbe lanciare un nuovo meme: sai quanti secondi ci sono in 6 settimane? 10!
Facciamo due conti:
60 secondi × 60 minuti × 24 ore × 7 giorni × 6 settimane = (4 × 3 × 5) × (2 × 3 × 10) × (3 × 8) × 7 × 6
Raggruppando in modo diverso i fattori, si ha:
2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 = 10!
2. Per rendere più immediata la sensazione di crescita dei fattoriali, si pensi a un mazzo di 52 carte francesi. I possibili differenti modi di disporle sono 52! ≅ 8 × 1067. Se ipotizzassimo che in una normale giornata, ci fosse in giro per il mondo un miliardo di tavoli in azione, ciascuno con 100 mani di qualche gioco, avremmo 1011 rimescolate di carte. In un milione di anni avremmo 365 × 106 giorni, con la possibilità quindi di effettuare 3,65 × 1019 rimescolate. Ebbene, le rimescolate risultanti sarebbero una frazione di 1 su 2 × 1048 , con un’elevatissima possibilità, quindi, di avere mani tutte diverse.
E se si usassero le 40 carte napoletane? In questo caso le possibili differenti rimescolate sarebbero poco più di 8 × 1047, molte meno quindi. Ma, con la stessa intensità di gioco ipotizzata per le carte francesi, in un milione di anni si effettuerebbe una frazione di 1 su 2 × 1028 , comunque abbastanza piccola da potersi attendere mani tutte diverse.
Quanti zeri finali ha il fattoriale di n?
Dalla tabella appena riportata si vede che al fondo del fattoriale si accumulano degli zeri. Questo fatto ispirò un problema proposto nella rubrica di matematica ricreativa, pubblicata verso la fine degli anno ’60 dalla rivista Oggi (vado a memoria, ma dovrebbe trattarsi proprio di Oggi).
Calcolare quanti zeri finali ha 100!
Ogni zero è dovuto alla presenza di un 2 e di un 5 tra i fattori di n!.
Ora, di fattori 2 se ne accumulano in abbondanza: da 1 ad n, infatti, un numero ogni due è pari. Sono più rari i 5. Quindi per contare gli zeri in n! basterà contare quanti 5 sono presenti come fattori dei numeri da 1 a n.
Esempio: da 1 a 34, avremo che: 5, 10, 15, 20, 25 e 30 sono multipli di 5. Ognuno porta un fattore 5, ma 25 ne porta due. Quindi mi aspetto 6 + 1 = 7 zeri finali. E infatti 34! = … 609.643.520.000.000.
Quanti zeri avrà allora 100! ?
Contiamo i multipli di 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100. Sono in tutto 20. In più, 25, 50, 75 e 100 hanno un ulteriore fattore 5. Quindi mi aspetto: 20 + 4 = 24 zeri finali.
Una ricerca su Google ci offre una tabella dei fattoriali dei primi 1.000 numeri, che ci fornisce:
100! = 93.326.215.443.944.152.681.699.238.856.266. 700.490.715.968.264.381.621.468.592.963.895. 217.599.993.229.915.608.941.463.976.156.518. 286.253.697.920.827.223.758.251.185.210.916. 864.000.000.000.000.000.000.000.000
Chi avesse voglia di sviluppare il ragionamento, può divertirsi con 1.000!, che di zeri ne ha 249.
Logica di funzionamento del file di calcolo dei fattoriali
Un calcolo diretto in Excel, utilizzando la funzione fattoriale(n), va in crisi con il fattoriale di 21, che viene calcolato come:
51.090.942.171.709.400.000, invece di 51.090.942.171.709.440.000
La precisione necessaria va quindi realizzata mediante un algoritmo più articolato, realizzato nel file Excel per il calcolo dei fattoriali.
Il file si compone di tre fogli:
- “calcolo“: le colonne da C a O ospitano 13 gruppi di tre cifre, dando quindi la possibilità di arrivare fino a 39 cifre totali per il fattoriale; ogni cella è calcolata come resto a 1.000 della corrispondente cella della riga precedente, moltiplicata per il numero n (in colonna A) di cui si sta calcolando il fattoriale; il quoziente intero della divisione per 1.000 viene invece trasferito alla colonna adiacente a destra (il riporto di scolastica memoria;
- “generatore“: nelle colonne da C a O, le corrispondenti celle del foglio “calcolo” vengono tradotte nella porzione di fattoriale da visualizzare, lasciando la cella vuota quando è necessario, aggiungendo gli zeri che servono e il puntino di separazione delle migliaia dove va inserito;
- “fattoriale“: le porzioni di fattoriale vengono assemblate nell’ordine giusto (dalla colonna O alla colonna C) e viene anche calcolato il numero di cifre dei vari fattoriali.
Si sarebbe potuto realizzare con meno fogli? Sicuramente sì, a costo però di complicare decisamente le formule. Si può estendere a un numero maggiore di cifre? Con un po’ di pazienza, sì. Nei primi due fogli basta aggiungere le colonne volute oltre la O, le righe necessarie, e infine estendere le formule, copiandole. Per il terzo foglio basta modificare la formula di assemblaggio del fattoriale ed estendere le righe.
Esiste un algoritmo più semplice? Scommetterei di sì, ma a me non è venuto in mente, almeno non ancora!
Foto di Gerd Altmann da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.