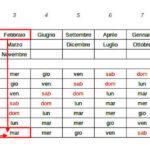
Qualche anno fa, correva il 2013, pubblicai sul mio blog Elaborando un calendario dell’Avvento matematico. Un dubbio che mi è sempre rimasto è se le caselline del calendario dell’Avvento debbano essere 24 o 25 (incluso quindi anche il giorno di Natale). Nel dubbio, mi tenni largo.
Una fatica boia trovare sul web 25 quiz basati su numeri, geometria o logica, che avessero il giusto grado di complessità: né troppo facili, né troppo complicati. E che, inoltre, fossero carini.
Ho ripescato una manciata di quei quiz, che ripropongo in questo articolo.
Ma il primo dicembre è lontano – penserà qualcuno. Beh, vorrei far notare che al supermercato sono già spuntati i panettoni, quindi il mio anticipo appare legittimo.
Le soluzioni seguiranno nei commenti, ma non subito!
PS: il mio Elaborando è fermo al post del 24 maggio del 2016. Chissà che, prima o poi, non riprenda vita.
Calendario dell’Avvento matematico: primo quiz!
Il primo quiz che ripropongo era stato prelevato da un sito norvegese. A quell’url oggi c’è una re-direzione a un sito che tratta comunque di quesiti matematici per la gioventù. Ho qualche difficoltà con il norvegese, non saprei ritrovare la pagina del quiz, ammesso che sia ancora sul sito. Comunque il quiz era questo:
Due anni fa, Petter aveva tre volte l’età di Ulrik. In due anni, Ulrik avrà solo la metà degli anni di Petter. Qual è la somma attuale dell’età di Ulrik e di Petter?
Ci sono almeno due modi per risolvere il problema: uno con la classica coppia di equazioni con due incognite, l’altro basato su una rappresentazione grafica delle età dei due ragazzi.
Secondo quiz: logica e dadi
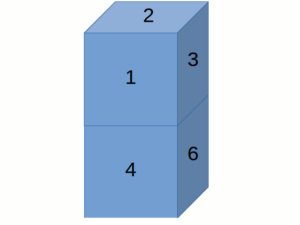Questione semplice, se si hanno a disposizione due dadi uguali. In caso contrario, occorre andare di logica.
Sul tavolo due dadi, uguali tra loro, sono sistemati uno sull’altro, come in figura.
Ricordando che la somma dei valori delle facce opposte di un dado è sempre pari a 7, con quale faccia poggia sul tavolo il dado inferiore?
Un piccolo aiuto per la soluzione:
- primo passo: che valore hanno le facce nascoste del dado posto in alto?
- secondo passo: quali sono i valori possibili per la faccia che poggia sul tavolo?
- ma i dadi sono uguali! Quindi…
Terzo quiz: fattoriali
In matematica n! indica il prodotto di tutti i numeri interi, da 1 fino a n. Esempio: 6! = 1 * 2 * 3 * 4 * 5 * 6 = 720.
A introdurre questa annotazione compatta fu Christian Kramp, matematico francese vissuto a cavallo del 1800.
I fattoriali sono numeri ricchi di fattori primi. Nel nostro esempio: 720 = 24 * 32 * 5.
Per cominciare, n! ha come fattori tutti i numeri primi tra 1 e n. Peraltro quelli maggiori di n ovviamente mancano. E poi ha un sacco di 2, basti pensare che, un numero sì e uno no, si aggiunge uno o più 2 ai fattori di n!.
Fatte queste premesse, se n! = 215 * 36 * 53 * 72 * 11 * 13, quanto vale n?
Dovrebbe essere facile rispondere, senza fare nemmeno troppi calcoli.
Quarto quiz
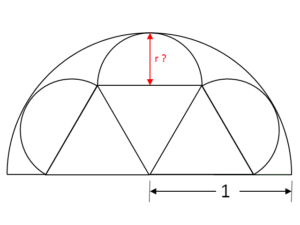Nell’immagine qui a lato è riportata una figura geometrica composta da tre semicerchi costruiti sui lati di tre triangoli equilateri uguali, e completata dal semicerchio esterno, su cui poggiano i triangoli equilateri, e che è tangente ai tre semicerchi.
Se il raggio del semicerchio esterno misura 1, quanto misura il raggio r dei tre semicerchi interni?
Questo problema è un esempio di come la figura che accompagna il testo possa facilitare oppure offuscare la strada verso la soluzione.
Nel disegno, infatti, se si evidenziasse il raggio del semicerchio maggiore (1) in una diversa posizione, sarebbe molto più semplice individuare la strada per la soluzione.
Quinto quiz
Il nostro sistema di numerazione è un sistema posizionale, su base 10. Vuol dire che con 10 simboli (le cifre da 0 a 9) e le potenze successive di 10, possiamo rappresentare qualunque numero. Ad esempio, 123 rappresenta il numero 1 × 102 + 2 × 101 + 3.
Perché 10 ? La natura ci ha fatto con cinque dita per mano, è quindi venuto naturale aiutarsi a contare grosse quantità di oggetti con le due mani, cioè con 10 dita. Quelle pecore laggiù? Sono 2 volte le due mani, più altre 3. Un piccolo passo di sintesi e diventano XXIII. Un altro passo ed eccoci a 23.
Con 6 dita per mano ci saremmo trovati molto meglio a fare di conto: 12 ha molti più divisori di 10 e ci saremmo semplificati la vita nel maneggiare le frazioni. Ci hanno provato in molti, come dimostra, per fare un esempio, la misura del tempo in minuti e secondi (60 = 12 × 5, arriva dai Babilonesi). E le uova? vanno a dozzine, tranne a Livorno dove si comprano a coppie.
L’informatica ci ha portato poi altre basi di numerazione: 2, poi 8 (abbandonata) e 16.
Un esempio: 123 (base 16) = 1 × 162 + 2 × 161 + 3 = 291 (base 10).
Ed eccoci al quiz:
In quale base di numerazione x l’intero positivo 1254 (base x), una volta raddoppiato, dà come risultato 2541 (base x)?
Si può risolvere sia con una classica equazione che con passaggi logici.
Sarà venuta a qualcuno l’insana voglia di preparare un Calendario dell’Avvento matematico ai propri figli o nipoti? Penso di no, forse non sarebbe nemmeno una buona idea. Meglio, probabilmente, l’approccio di mia figlia Valentina con la piccola Luna, che si avvicina ai 4 anni: dolcetti, giochini e qualche attività divertente da svolgere con mamma o papà, nei momenti strappati al lavoro e alle faccende di casa.
Però un giochino proverei a inserirlo, se solo me lo consentissero.
L’immagine di apertura dell’articolo è di Pixaline, da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
Articoli correlati:
