La spirale di Ulam è una curiosa rappresentazione grafica dei numeri primi, creata nel 1963 dal matematico polacco Stanislaw Ulam.
Durante un incontro di lavoro, si ritrovò infatti a riportare i numeri naturali (1, 2, 3, …) su un foglio di carta, disponendoli lungo una spirale immaginaria. Partendo da un punto centrale del foglio, la spirale si avvolgeva via via in una disposizione completamente diversa da quella della scrittura naturale da sinistra a destra.
La sorpresa si materializzò quando Ulam marcò i numeri primi, per farne risaltare la posizione sulla griglia: i primi tendevano a disporsi infatti sulle linee diagonali dello schema dei numeri.
Non è ancora chiaro cosa questo fenomeno possa rivelarci della natura per molti versi misteriosa dei numeri primi, ma certamente può essere interessante ripercorrere i passi di Ulam, questa volta con un computer a disposizione.
La spirale di Ulam al computer
Il modo più rigoroso per costruire una rappresentazione a computer della spirale di Ulam è quello di ricorrere a del codice di programmazione. Avrei potuto utilizzare il mio solito Ruby, o anche ricorrere a una macro su LibreOffice Calc (l’equivalente gratuito di Excel). La pigrizia del pomeriggio estivo mi ha spinto invece a una rappresentazione semi-automatizzata (ma praticamente manuale) su un foglio di calcolo. L’assenza di macro rende il file (scaricabile da qui) fruibile sia da LibreOffice Calc che da Excel.
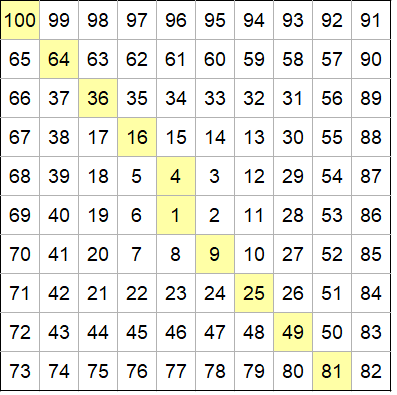
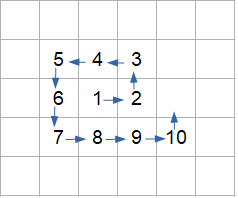Volendo costruire la spirale per i numeri primi minori di, ad esempio, 2.000, dovrò disporre i numeri da 1 a 2.000 in un quadrato, il cui lato sarà almeno pari alla radice quadrata di 2.000. Il quadrato avrà quindi il lato di 45 celle. Questo mi suggerisce la posizione della cella da cui far partire la spirale: più o meno in riga 23, colonna 23. Pigrizia per pigrizia, ci si può poi aggiustare strada facendo.
Inserito il numero 1, punto di partenza della spirale, ho inserito nella cella immediatamente a destra la formula:
= <cella_a_sinistra> + 1
per ottenere 2, il numero successivo. Poi nella cella appena sopra il 2, la formula:
= <cella_sotto> + 1
per ottenere 3. In modo del tutto analogo ho ottenuto il 4, completando il primo quadrato (1, 2, 3, 4).
A questo punto ho esteso la formula dalla cella del 4 a quella alla sua sinistra (5), poi nella cella sottostante ho inserito la formula:
= <cella_sopra> + 1
per ottenere 6 e, estendendo in basso, per ottenere 7.
Partiamo con la spirale!
Da questo punto in avanti è sufficiente disegnare la spirale ripetendo via via i tre passi:
- copia la formula dell’incremento dal vicino del giro di spirale precedente;
- seleziona le celle da popolare, nella direzione giusta;
- incolla la formula.
Il riempimento della spirale procede all’inizio molto lentamente, poi, aggiungendo giri alla spirale, si accelera progressivamente. Il risultato è una cosa come quella mostrata in figura.
Essendo il procedimento essenzialmente manuale, è bene verificare di tanto in tanto di non aver commesso errori. Per farlo basta controllare che al completamento dei vari quadrati concentrici ci siano in progressione i quadrati dei numeri naturali, i pari da un lato e i dispari dall’altro.
Bene, la spirale è compilata.
Come evidenziare i numeri primi
In un lavoro di programmazione ben concepito, i numeri primi andrebbero calcolati. Ma, nella mia personale giornata dedicata alla pigrizia, ho preferito scaricare dal Web la lista dei numeri primi che mi occorreva. Sempre per pigrizia ho inserito la lista nel file excel così com’era (foglio “primi“), con i primi fino a 5.000, anche se me ne servivano di meno. Una volta avrei detto: «Per sviluppi futuri ».
A questo punto, duplicato il foglio con la spirale (che ho chiamato “interi“), nel nuovo foglio ho sostituito in ogni cella le formule generatrici della spirale con una formula che lascia visibile il numero solo se è primo. Esempio, nella cella B2 ho inserito la formula:
=SE.ERRORE(CERCA.VERT(interi!B2;primi!$A:$A;1;0);””)
Anche questa operazione è decisamente semplice: si inserisce la formula nella cella nel vertice in alto a sinistra e la si ricopia in lungo e in largo nel quadrato.
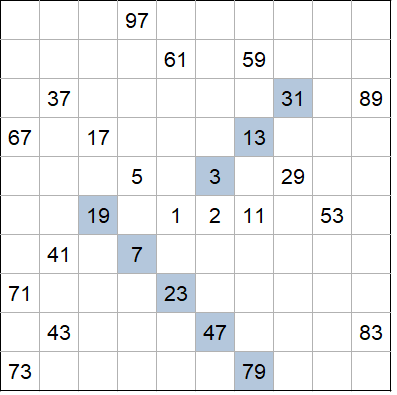
Nel quadrato ho evidenziato i numeri primi disposti lungo diagonali, si nota subito una sequenza di 5 primi (19, 7, 23, 47, 79). Non è invece una sequenza da 5 primi l’altra evidenziata perché (3, 13, 31) non è ricongiungile al 7 dal momento che 1 non è un numero primo.
Quanto possono essere lunghe le sequenze?
Inizialmente avevo compilato la spirale fermandomi a 1.000, e avevo notato diverse sequenze di lunghezza 5, la massima presente.
Volendo capire se possa esserci un limite implicito, il primo passo da effettuare è ampliare nel limite del fattibile la spirale, e vedere cosa succede.
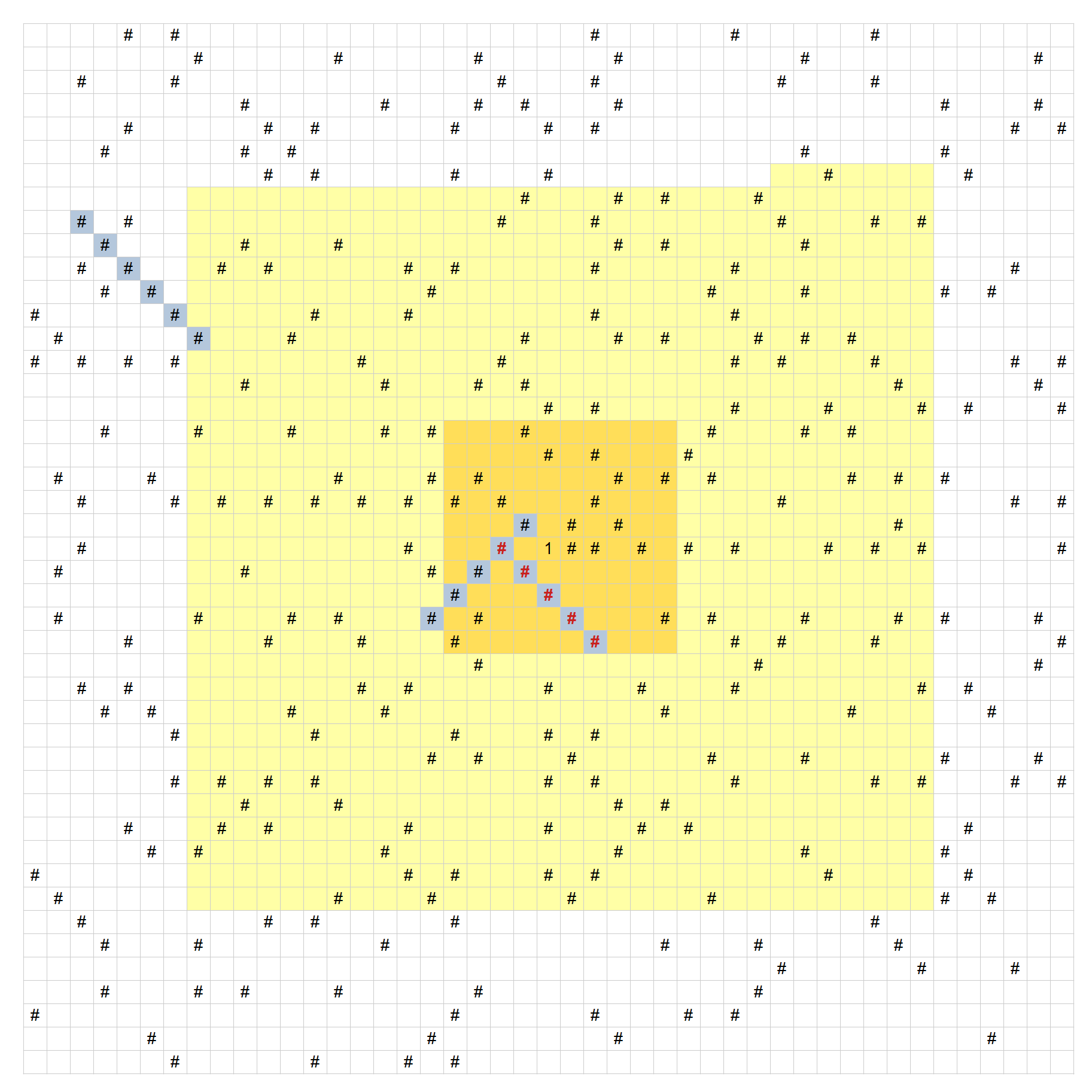
Per rendere leggibile la tabella ho preferito sostituire i numeri con dei caratteri “#“. Ho poi evidenziato il campo dei primi 1.000 numeri, e alcune sequenze individuate.
Tirando le somme
Nell’immagine è evidenziato anche il quadratino centrale con i primi 100 numeri. Interessante vedere come una sequenza di 4 in questo quadrato si è poi rivelata essere da 5.
Riguardo alla domanda iniziale (potrebbe esserci un limite a 5 numeri primi in sequenza?), la risposta è evidentemente no, visto che in alto a destra c’è una sequenza da 6.
A questo punto vengono curiosità sulla spirale di Ulam che è complicato soddisfare con un foglio di calcolo, se non altro per la difficoltà di cogliere “a occhio” le sequenze e la correlazione tra di loro. Mi sa che sarebbe meglio passare a del codice serio.
L’estate è ancora lunga, ci penso.
Foto di apertura di Gerd Altmann, da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
Articoli correlati:
