La sequenza o congettura di Collatz ha il fascino delle domande semplici a cui nessuno ha ancora dato una risposta.
Nota anche come congettura di Ulam o di Thwaites, capita di incontrarla inoltre come problema di Kakutani o di Syracuse, oppure come algoritmo di Hasse, o infine come sequenza della grandine (hailstone).
Tanti nomi diversi testimoniano un grande interesse per la questione, nata negli anni ’30 del secolo scorso ma con larga diffusione in campo matematico solo a partire dagli anni ’60.
Come funziona la congettura di Collatz?
Costruiamo una sequenza a partire da un numero intero positivo, dividendolo per 2 se è pari, oppure moltiplicandolo per 3 e sommando 1 se è dispari. Partiamo, ad esempio da 11:
11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
Da qui la sequenza si ripete in un ciclo infinito: 1 → 4 → 2 → 1 → 4 …
Provando con un po’ di numeri diversi, si osserva lo stesso comportamento: dopo un po’ di su e giù, la sequenza precipita incontrando numeri pari divisibili più volte per 2 (nell’esempio: 40, poi 16). E alla fine atterra su 1.
La congettura di Collatz consiste nell’ipotizzare che questo avvenga per tutti i numeri interi positivi.
Il comportamento delle sequenze ricorda la formazione della grandine. Nuclei di ghiaccio portati su dalle correnti ascensionali e giù dal proprio peso, si aggregano tra loro fino a diventare troppo pesanti e precipitare al suolo. Da qui il nome di sequenza della grandine, in inglese hailstone sequence.
La formulazione della congettura di Collatz
La congettura di Collatz fu formulata negli anni ’30 del ‘900 dal matematico tedesco Lothar Collatz. A oggi la questione è ancora aperta, in attesa di essere dimostrata vera o confutata.
Nel tempo molti matematici hanno provato a fornire una risposta rigorosa, spinti dall’apparente semplicità della domanda. Ma il problema si è rivelato ostico. Quanto ostico?
Un’idea ce la fornisce la valutazione del matematico ungherese Paul Erdős. Solito offrire a colleghi e studenti una ricompensa economica per la soluzione dei problemi che proponeva, il premio partiva da pochi dollari per problemi che impegnano duramente anche esperti. Arrivò a 50$ per un problema ancora oggi irrisolto (frazioni egizie, ne scriverò prima o poi qui). A chi avesse fornito un risposta alla congettura di Collatz, Erdős offrì invece 500$. Il suo intuito gli suggeriva che servisse una matematica ancora da scoprire.
Matematico dalle mille collaborazioni, Paul Erdős si spostava da una casa all’altra, ospite dei suoi colleghi, senza avere fissa dimora. I suoi effetti erano in due vecchie valigie che portava con sé negli spostamenti.
Another roof, another proof era il suo motto (Un nuovo tetto, una nuova dimostrazione).
Una prima analisi della congettura di Collatz
Una sequenza di Collatz potrebbe comportarsi in tre modi distinti:
- precipitare a 1, dopo aver altalenato su e giù come nell’esempio riportato; la congettura di Collatz suppone che questo si verifichi per ogni numero intero positivo;
- terminare su un ciclo diverso da 4 → 2 → 1→ 4 (…) ;
- divergere, toccando numeri sempre maggiori e non terminando mai né a 1, né in un ciclo.
Una congettura (caso 1) può essere dimostrata vera o falsa, in base ad un rigoroso ragionamento logico-matematico, oppure confutata trovando un controesempio (casi 2 o 3).
Entrambe le strade vengono attivamente esplorate da più di 50 anni, senza che sia stata trovata né una dimostrazione, né un controesempio. È stato verificato ad oggi che tutti gli interi positivi fino a 5 x 260 terminano infatti, prima o poi, a 1 (per farsi un’idea del numero, basta una ricerca su Google).
In alcuni casi il percorso è particolarmente lungo, tenendo conto del numero da cui si è partiti. Ad esempio, partendo da 27 si arriva a 1 dopo un percorso di ben 112 passi. Nel suo viaggio la sequenza sale fino a 1.780, ridiscende a 167, si impenna fino a 9.232, per poi scendere più o meno a capofitto verso 1.
Quali strade sono state battute dai ricercatori, alla ricerca di regolarità, che diano la chiave di risoluzione? Il primo passo è farsi un’idea di come varia la lunghezza della sequenza, in base al numero di partenza.
Esploriamo la congettura di Collatz
Si può cominciare dal generare con un programma, ad esempio in Ubasic (qui le istruzioni per installarlo sul pc), un elenco di dati in formato .csv, da analizzare poi con Excel o LibreOffice.
Un mio semplicissimo programma Ubasic che genera un file .csv con la lista dei numeri dispari da 3 a 50.001, con relativa lunghezza della sequenza, si può scaricare da qui.
In realtà il programma genera anche altri dati. Partendo, infatti, dall’osservazione che a un passo “dispari” segue necessariamente almeno un passo pari (es. 5→ 16), è possibile aggregare i due passi in uno solo, modificando il passo dispari in:
( n → (3n + 1)/2)
In questo caso si salterà il conteggio di un passo (pari) per ogni passo dispari presente nella sequenza. Quindi, se la sequenza di p passi pari e d passi dispari ha originariamente lunghezza p + d, quella ottenuta aggregando il primo passo pari è di p + d – d = p passi. Quindi la lunghezza riflette solo il numero di passi pari.
Si può aggregare in un solo passaggio anche gli eventuali dimezzamenti successivi. In questo modo nella sequenza rimangono solo i numeri dispari (11 → 17 → 13 → 5 → 1), e quindi la lunghezza della sequenza è uguale a d.
Quando negli anni ’60 il problema cominciò a girare tra le università statunitensi, i calcolatori non erano ancora diffusi come oggi. Il modo più comune per affrontare un problema come questo era ancora carta e penna.
L’apparente semplicità indusse molti a provarci, spendendo ore di calcoli senza cavare un ragno dal buco.
Con un pizzico di ironia qualcuno ipotizzò che la congettura facesse parte di una cospirazione sovietica, intesa a paralizzare la ricerca matematica statunitense.
Qualche grafico sulla congettura di Collatz
Se effettivamente tutte le sequenze portano a 1, allora gli interi positivi dovrebbero disporsi secondo un albero, con radice in 1. Le diramazioni dovrebbero passare, prima o poi, per tutti i numeri interi positivi. Questo tipo di costruzione mostra delle regolarità, ma non ha fornito ad oggi lo spunto desiderato.
Qui di seguito alcune esplorazioni, replicate nel file Excel scaricabile da qui.
Nell’ordine:
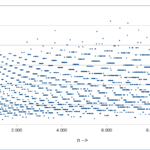
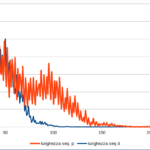
- la lunghezza delle sequenze di Collatz per i numeri dispari minori di 10.000. Si osservano frequenti gruppetti di numeri vicini che hanno la stessa lunghezza. Poiché due numeri dispari consecutivi non hanno fattori primi in comune, si tenderebbe a escludere un legame tra lunghezza della sequenza e fattori primi;
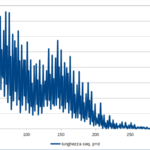
- distribuzione delle lunghezze per i numeri dispari minori di 10.000. La gobba che si nota intorno alla lunghezza di 120 è (purtroppo) fuorviante, si livella analizzando più numeri;
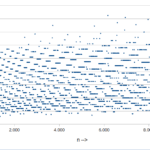
- numero di passi pari, che come visto è la lunghezza della sequenza che aggrega il passo 3n + 1 con il successivo dimezzamento. L’andamento è simile a quello visto nella fig. 1 perché…
- …il numero di passi pari e quello dei passi dispari sono correlati: se la sequenza arriva ad 1, i primi devono compensare in diminuzione l’effetto dei secondi in aumento. Il grafico mostra l’andamento del rapporto p/d, e…
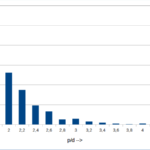
- …la distribuzione di p e di d;
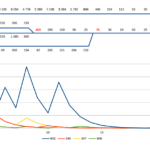
- un gruppo di numeri dispari consecutivi con la stressa lunghezza di sequenza: 943, 945, 947, 949. Si noti l’ampiezza del viaggio di 943 e come invece 949 proceda piatto.
Altre esplorazioni della congettura di Collatz
Altri hanno provato ed estendere l’analisi ai numeri interi negativi (a volte, allargando l’obiettivo, entrano nella visuale elementi nuovi). Altri ancora hanno provato ad esaminare le sequenze in cui il passo dispari è ottenuto triplicando e sottraendo 1 ( n → 3n -1).
A oggi la sfida è ancora aperta. Basta un piccola conoscenza di programmazione per divertirsi a generare sequenze e osservarne il comportamento. Dopo 50 e passa anni di ricerche è difficile che esista una prova o una confutazione della congettura a portata di mano, ma il divertimento è assicurato.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.