C’è irrazionale e irrazionale, mi fa notare, in modo molto semplice e ingegnoso, un recente articolo su Slate. L’articolo mostra infatti come costruire un’immagine. simile a un codice a barre, che evidenzia con immediatezza quanto un numero irrazionale possa essere approssimato con una frazione semplice.
Qui si intende per frazione semplice una frazione in cui sia il numeratore che il denominatore sono numeri con poche cifre (definizione che dal punto di vista matematico fa rabbrividire).
È il caso di π, approssimato a meno di due milionesimi dalla frazione 355 ⁄ 113 dal matematico e astronomo cinese Zu Chongzhi, vissuto tra il 429 e il 500. Allo stesso risultato sarebbe poi arrivata anche la matematica occidentale, ma solo un migliaio di anni dopo.
Nell’articolo di Slate si confronta appunto il codice a barre di π con quello di φ, il rapporto aureo. Sorpresa: φ si comporta in modo molto diverso, segnalando quindi di non avere una buona approssimazione mediante una frazione semplice. Evviva, quindi, l’irrazionalità profonda di φ.
Mi è però venuto il dubbio che ad essere rara sia la proprietà di π, non quella di φ. Poche righe di Python mi hanno consentito di verificare.
Razionale e irrazionale
Un breve richiamo della matematica delle medie. Un numero è razionale quando può essere rappresentato da una frazione. Esempio: 3, 0,5, 0,3333… sono numeri razionali, potendoli rappresentare rispettivamente come 3, 1 ⁄ 2, 1 ⁄ 3.
In caso contrario il numero si dirà irrazionale. Esempio: √2, π sono numeri irrazionali, in quanto nessuna frazione può avere esattamente lo stesso valore. Vale la pena di ricordare la leggenda legata alla scoperta dell’irrazionalità di √2, con Pitagora che condanna all’esilio in mare, con conseguente morte per naufragio, dello scopritore dell’irrazionalità nei numeri, Ippaso di Metaponto.
Il codice a barre di un numero
Si immagini di riportare su un asse orizzontale la parte decimale di un numero e quella di un buon numero dei suoi multipli dal doppio a salire.
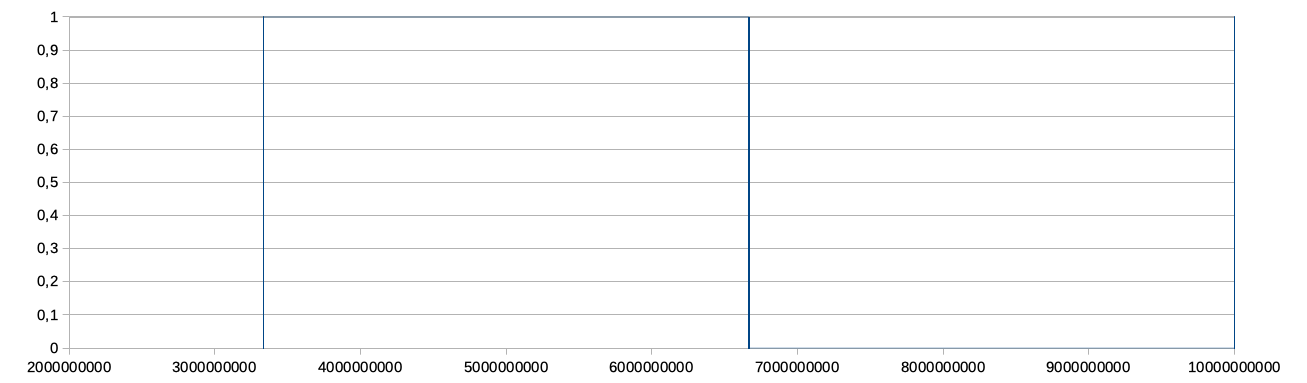
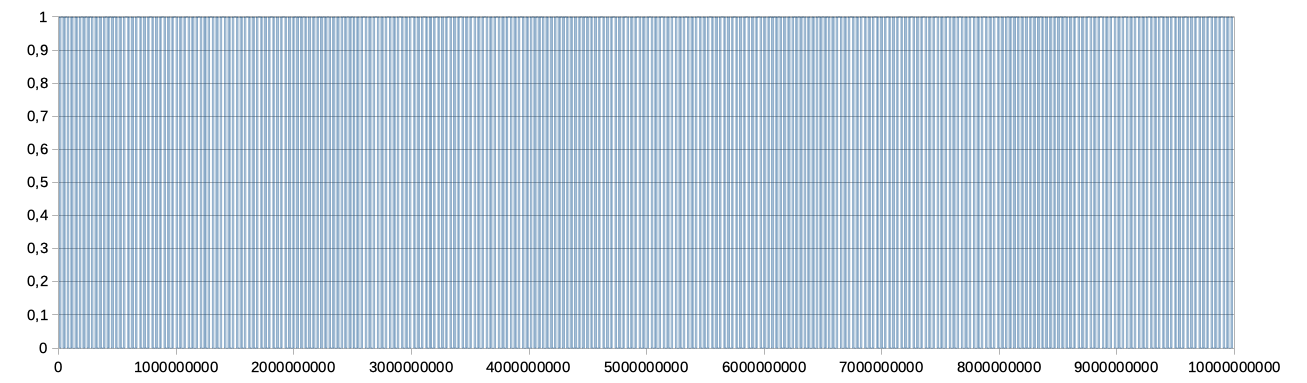
Esempio: posto x = 1 ⁄ 3, riportiamo sull’asse la parte decimale di x, 2x, 3x, … 999x. In corrispondenza di ogni valore, tracciamo un breve tratto verticale di lunghezza fissa. Si ottiene un’immagine così:
Si evidenziano solo tre barre, su cui vanno ad accumularsi i 1.000 valori rappresentati nel grafico: in corrispondenza di 1 ⁄ 3, 2 ⁄ 3 e di circa 1.
Breve spiegazione del grafico: sull’asse delle x è riportato il valore della parte decimale di x e dei suoi multipli, troncata a 10 cifre. Per esigenze di calcolo ho approssimato 1 ⁄ 3 con 0,3333333333, troncando il valore, per difetto, alla decima cifra decimale. Questo fa sì che la terza barra che dovrebbe essere in realtà posta a 0, sia invece vicinissima a 1.
Il perché del grafico è semplice. Prendiamo ad esempio il caso del multiplo 53 × 1 ⁄ 3 = (51 + 2) × 1 ⁄ 3 = 17 + 2 ⁄ 3. La parte decimale di questo multiplo sarà quindi 2 ⁄ 3. Analogamente, per gli altri multipli il risultato non potrà che essere 0, 1 ⁄ 3, 2 ⁄ 3.
Cosa avviene con altre frazioni?
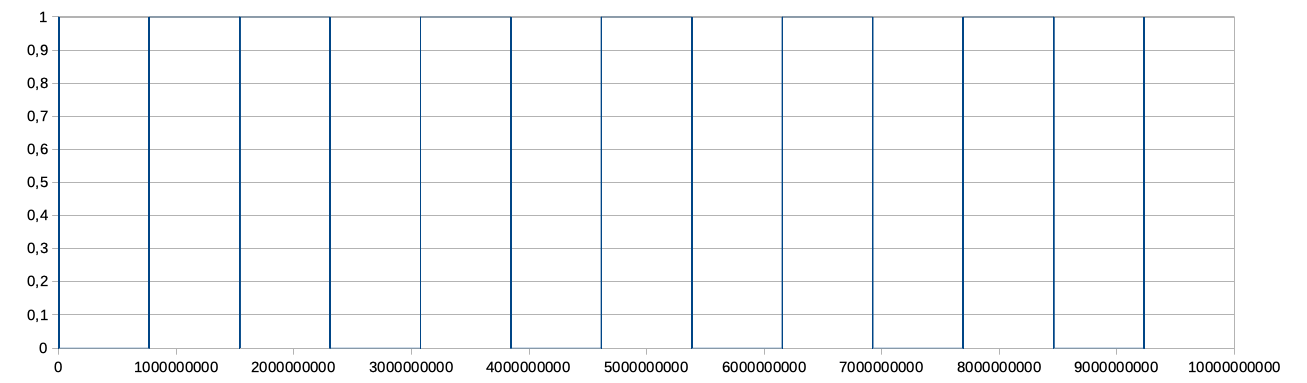
Prendiamo ad esempio la frazione 11 ⁄ 13. Il suo codice a barre presenta 13 barre verticali:
Le 13 barre verticali sono in corrispondenza di 0, 1 ⁄ 13, 2 ⁄ 13, … 12 ⁄ 13. Il numeratore (11) non ha effetto sul grafico.
Come ho elaborato il codice a barre
Bastano poche righe di codice Python per calcolare la lista dei valori da riportare poi in un grafico LibreOffice Calc o Excel.
s = 18461538462 # 1 + 11/13
n_dec = int(math.log10(s))
lista = []
print ("costante:",s/10**n_dec)
print ("numero_di cifre_decimali:",n_dec)
print ("decimali dei multipli:")
for k in range(1,1000):
lista.append(str(k*s)[-n_dec:])
y=0
for i in sorted(lista):
print (i,y)
y = 1 - y
print (i,y)
Nella prima riga il valore impostato per il numero di partenza è 1 + 11 ⁄ 13, e non 11 ⁄ 13 solo per evitare di verificare (pigrizia pura) il comportamento del codice a fronte di numeri con una parte intera uguale a 0 (come per 11 ⁄ 13) oppure diversa da 0 (come per π = 3,14159…). La forma del codice a barre non è impattata.
Irrazionale ma non troppo: π a confronto con φ
Ci si potrebbe immaginare che, per un numero irrazionale, la componente decimale sia caotica, senza una struttura periodica come avviene per i numeri razionali. E quindi che la parte decimale dei suoi multipli tenda a distribuirsi uniformemente tra i valori 0 e 1.
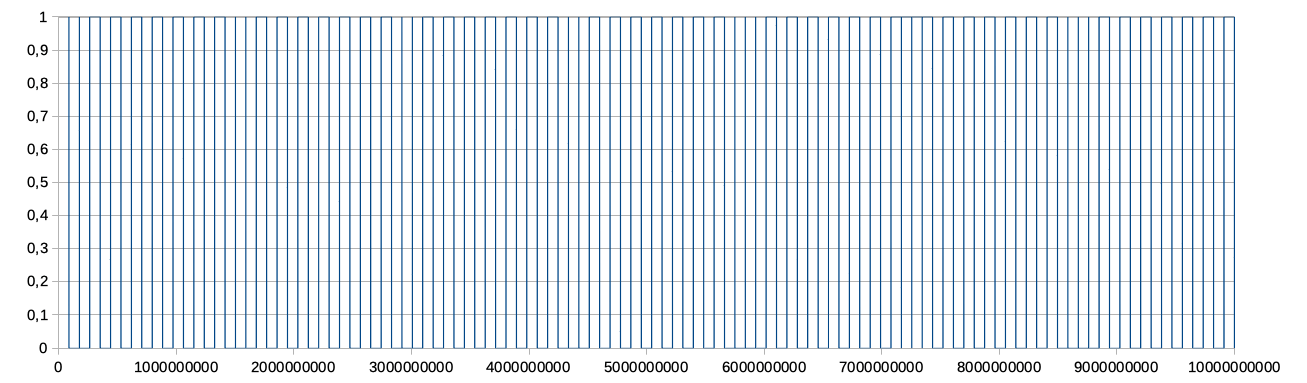
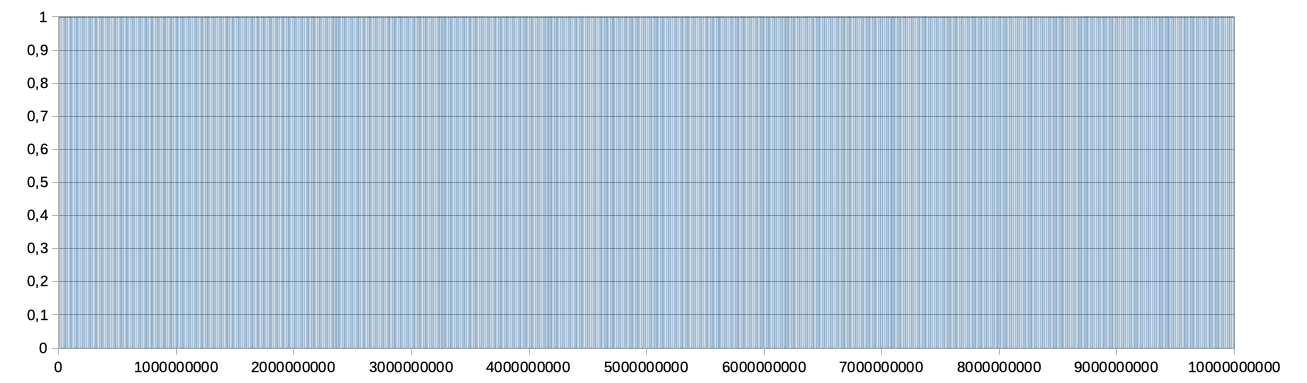
Non è sempre così. Di seguito riporto i codici a barre di π e φ (rispettivamente pi greco = 3,14159 … e Rapporto Aureo = 0,61803…)
Nel caso di π il codice a barre è molto vicino a quello di una frazione. Le barre dovrebbero essere 113 (non ho avuto la costanza di contarle a mano).
Per il rapporto aureo φ, invece, le barre si dispongono ben distribuite, a meno di piccoli addensamenti di cui mi risulta però difficile cogliere la regolarità.
Cosa avviene per altre costanti irrazionali note?
Ho provato a costruire il codice a barre per altre costanti note: e (numero di Eulero o di Nepero), √2, la costante di Apéry.
In tutti i casi il codice si presenta simile a quello del rapporto aureo, a sottolineare che π è un caso a sé, con una natura per certi versi più simile a un numero razionale.
Riporto solo il codice a barre per Apéry:
Anche qui si notano degli addensamenti più o meno regolari, ma il caso è ben diverso rispetto a π.
Un caso particolare
Una verifica della correlazione tra approssimazione frazionaria della costante e sua rappresentazione via codice a barre l’ho trovata nel caso della costante irrazionale di Cahen.
L’ho scoperta per caso, frugando nella lista delle costanti note, alla ricerca di una che avesse una buona approssimazione razionale.
In effetti un’ottima approssimazione si trova troncandone ai primi 5 termini la serie generatrice:
1 – 1 ⁄ 2 + 1 ⁄ 6 – 1 ⁄ 42 + 1 ⁄ 1806 = 83 ⁄ 129
L’immagine richiama quella di π, con la differenza che abbiamo 129 barre al posto di 113. Il che sottolinea il carattere di eccezionalità di π.
Ma è meglio la razionalità o l’irrazionalità?
Anni fa avevo trovato questa divertente interpretazione della differenza tra razionalità e irrazionalità.
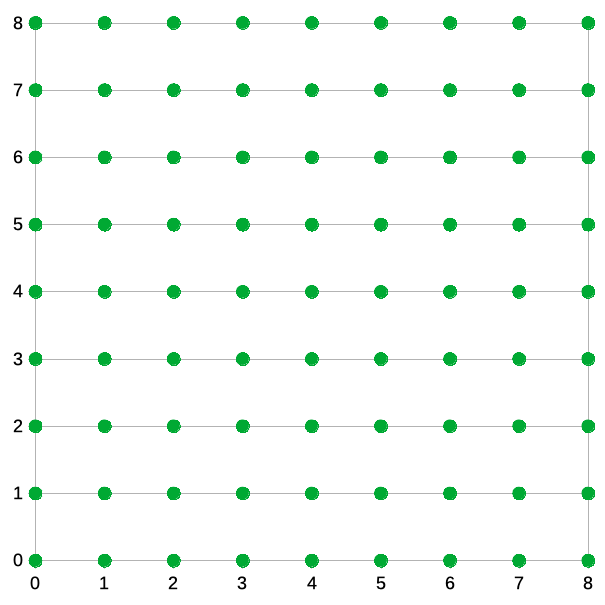
Si immagini di avere un bosco infinito, con alberi puntiformi piantati in punti ben precisi su un reticolo a maglia quadrata con lato pari a 1. La figura che segue ne riporta un pezzo:
Se ci si pone nel punto di coordinate (0,0) e si guarda in una direzione razionale, una direzione cioè in cui la componente orizzontale e quella verticale siano in un rapporto frazionario, il nostro sguardo si fermerà sull’albero posto proprio nel punto corrispondente a quella frazione.
Se, viceversa, la direzione è irrazionale, allora nessun albero si troverà lungo la linea del nostro sguardo e si potrà esplorare fino all’infinito.
Una volta di più, quindi, ogni tanto ci vuole un momento di irrazionalità, se vogliamo uscire dalla rigidità degli schemi.
Immagine di apertura di Andrew Martin, da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.