Indovinello dei travasi, quando la matematica diverte

Alzi la mano chi non si è mai imbattuto nell’indovinello dei travasi: avete a disposizione due recipienti non graduati e di capacità diversa (esempio: 3 e 5 litri), e dovete ricavare una quantità esatta di liquido, diversa dalla capacità dei due recipienti (esempio: 4 litri).
Vediamo come si affronta l’indovinello e come realizzare con Excel un Risolutore universale. Un modo divertente per ripassare, o scoprire, qualche interessante formula di Excel.

L’indovinello

In una scena del film Die Hard – Duri a morire, Bruce Willis e Samuel L. Jackson, alle prese con una bomba da disinnescare, devono ottenere esattamente 4 galloni con l’aiuto di due taniche, una da 3 e l’altra da 5 galloni.
Ci riusciranno, ovviamente all’ultimo secondo, dopo aver capito la corretta sequenza di riempimenti, travasi e svuotamenti.

Non essendo pressati dall’emergenza del disinnesco, possiamo analizzare con tutta calma come utilizzare logica e matematica per trovare un algoritmo risolutore. Per poi passare alla sua realizzazione con Excel (o LibreOffice, il foglio elettronico Open Source compatibile con Excel).

L’impianto dell’indovinello è semplice. Sono disponibili:

due recipienti non graduati di capacità diversa;
tutto il liquido che si vuole.

Si possono inoltre svuotare a terra i due recipienti quando serve.

Esiste una versione equivalente dell’indovinello, in cui è dato un terzo recipiente, di capacità maggiore e pieno di liquido, da cui si può travasare nei primi due, e in cui questi possono essere svuotati.

Come si risolve questo tipo di indovinello? Partiamo da un po’ di logica

L’approccio tipico consiste in una serie più o meno casuale di riempimenti, svuotamenti e travasi, da cui si emerge o felici con la soluzione (e chi ricorda più qual è la sequenza?), oppure gettando la spugna.

Un pizzico di logica e uno di matematica forniscono invece la strada giusta.
Per praticità esaminiamo il problema di Die Hard, e cerchiamo un multiplo di 5 e uno di 3 che differiscano di 4.
Troviamo facilmente 5 (5 x 1) e 9 (3 x 3). Questo ci suggerisce che se riempiamo tre volte il contenitore da 3 e utilizziamo una volta il contenitore da 5 per svuotare, dovremmo rimanere con 9 – 5 = 4 galloni.
Chiamando A il contenitore da 5 e B quello da 3, ne segue che una sequenza che risolve è (tra parentesi riporto il numero di galloni spostati):

riempio B (3)
travaso in A (3)
riempio B (3)
travaso in A (2); A ora e pieno, in B è rimasto 1 gallone
svuoto A (5)
travaso in A (1)
riempio B (3)
travaso in A (3); in A ora ci sono 1 + 3 = 4 galloni

La soluzione è un po’ più lunga di quella di Willis e Jackson, ma funziona!

Tornando ai nostri multipli, troviamo ancora una coppia che funziona: 10 (5 x 2) e 6 (3 x 2).
Quindi possiamo questa volta riempire A due volte e svuotare B due volte. Vediamo la sequenza:

riempio A (5)
travaso in B (3); in A rimangono 2 galloni
svuoto B (3)
travaso in B (2); A ora e vuoto, in B ci sono 2 galloni
riempio A (5)
travaso in B (1); B ora è pieno e in A sono rimasti 5 – 1 = 4 galloni

Trovata! è la soluzione di Die Hard. Rimarrebbe da svuotare B, ma è chiaramente superfluo.

E un po’ di matematica

Quello che abbiamo fatto è cercare soluzioni dell’equazione in due incognite: 5x + 3y = 4. Non fatevi ingannare dal segno +, x e y possono assumere anche valori negativi. In effetti abbiamo trovato le due soluzioni: x = -1, y = 3 e x = 2, y = -2.

Un’equazione di questo tipo, che si può generalizzare come: ax + by = c si chiama diofantea, dal nome del matematico greco Diofanto di Alessandria.
Per nostra fortuna è ampiamente studiata, e si dimostra che ha soluzioni (e in numero infinito) solo se c è multiplo del massimo comun divisore (MCD) di a e b.
Il risultato è interessante, perché ci dice che se i due recipienti hanno capacità espressa da numeri primi tra loro (MCD = 1), come è il caso di Die Hard, si trova un modo per isolare qualunque quantità, purché possa essere contenuta in uno dei due recipienti. Invece, ad esempio, con due contenitori di 8 e 6 litri (MCD = 2) non sarà mai possibile isolare una quantità dispari.

Il Risolutore in Excel: l’impostazione

Excel si presta a realizzare un semplice Risolutore dell’indovinello dei recipienti.

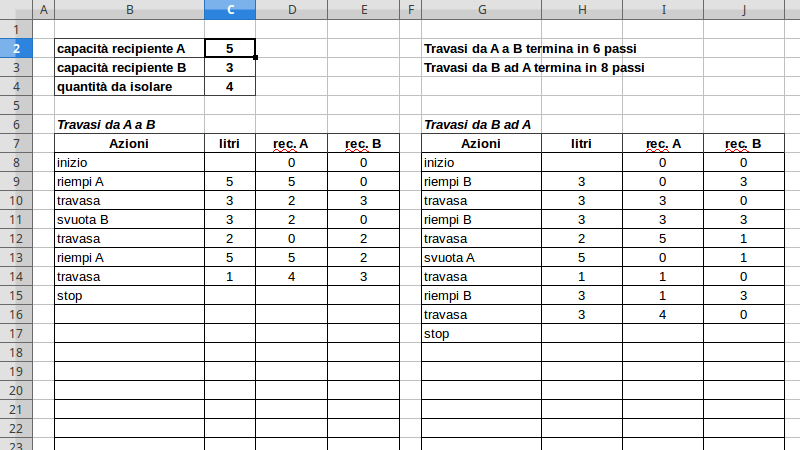
Nella figura è riportato come esempio la risoluzione dell’indovinello di Die Hard, per entrambe le strategie: travasi dal recipiente da 5 a quello da 3, e travasi dal recipiente da 3 a quello da 5.

Come per altri miei articoli di ricreazione matematica (ad esempio: Disegnare con il pc…), il file presentato è disponibile per il download. L’excel per questo articolo può essere scaricato da qui; la versione base è nel foglio “risolutore”.

Come si realizza il Risolutore?

Il primo passo è definire l’algoritmo. Come abbiamo visto ci saranno due possibili strategie: riempire A e svuotare B, oppure riempire B e svuotare A. Esaminiamo nel dettaglio la prima.

Il passo successivo è definire la struttura dei dati del Risolutore.
Nel nostro caso riportiamo in testa al foglio i dati dell’indovinello, cioè la capacità dei due recipienti A e B e la quantità di liquido da isolare. Variando questi dati sarà possibile simulare tutti i casi che si desidera.

Sotto impostiamo invece l’algoritmo vero e proprio, con delle formule che, una riga per volta, calcolano il passo da effettuare:

l’azione da compiere, scelta tra “riempi A”, “svuota B”, “travasa”, “stop”;
la quantità di liquido da spostare nell’azione;
il livello di riempimento di ciascuno dei due recipienti, dopo aver effettuato l’azione calcolata in questo passo.

Le formule sono le stesse per tutte le righe. Non esiste un meccanismo automatico per estenderle fin dove serve, quindi le formule sono da copiare manualmente in basso per un numero abbondante di righe.
Per rendere evidente il caso in cui il numero di righe attrezzate con le formule non sia sufficiente, adotto due accorgimenti:

le formule sono concepite in modo da lasciare in bianco le righe dopo lo stop;
le celle della zona attrezzata sono evidenziate con dei bordi.

In questo modo è immediato capire se lo spazio predisposto con le formule è sufficiente, oppure se occorre estenderlo, ricopiando le formule ancora per qualche riga.

Un breve ripasso di Excel

Il Risolutore si basa sulle operazioni di base di Excel, e su un paio di funzioni che torna utile ricordare:

= se(condizione; se-vero; se-falso)
Il valore restituito dalla funzione dipende dalla condizione: se è vera, viene restituito il secondo parametro (se-vero), altrimenti il terzo (se-falso).
= o(condizione1; condizione2;…; condizioneN)
Ritorna VERO (=1) se almeno una delle condizioni è vera; ritorna FALSO (=0), se tutte le condizioni sono false.

Delle operazioni base di Excel vale la pena rammentare tre cose:

una stringa va racchiusa tra una coppia di “ (esempio: “svuota A”);
una stringa vuota si identifica con “” ;
copiando una cella in un’altra, i riferimenti ad altre celle contenuti nelle formule si adattano automaticamente; per renderli invariabili si utilizza il carattere $ (ad esempio: C3 si adatta, mentre $C$3 rimane invariato; scrivendo C$3 si adatta solo la colonna).

Procedimento “travaso da A a B”: calcolo dell’azione

Nella prima riga riportiamo direttamente lo stato iniziale: scriviamo “inizio” nel campo dell’azione, lasciamo vuoto il campo della quantità di liquido da spostare, e impostiamo a 0 il riempimento dei due recipienti (sono inizialmente vuoti).

Nella seconda riga costruiamo la formula per calcolare l’azione necessaria (cella B9):

=SE(O(B8=”stop”;B8=””);””; …

Tradotto in umano: se il procedimento si è appena fermato, oppure era già fermo, lascialo fermo. Fin qui non dovrebbe essere difficile.

Al posto dei puntini sospensivi, la formula prosegue con l’azione da effettuare nel caso in cui il procedimento non sia ancora fermo:

SE(O(D8=$C$4;E8=$C$4);”stop”;…

Cioè: se uno dei due contenitori (D8, E8) ha raggiunto l’obiettivo ($C$4), fermati. Se non ci siamo ancora, i puntini sospensivi portano a:

SE(E8=$C$3;”svuota B”;…

Se il contenitore B è pieno, svuotalo, altrimenti:

SE(D8=0;”riempi A”; …

Se il contenitore A è vuoto, riempilo. Altrimenti (e siamo alla fine della formula, è il momento anche di chiudere le parentesi di apertura delle funzioni se):

“travasa”))))

Calcolo del liquido da spostare

Determiniamo ora la quantità di liquido da spostare, e proviamo a farlo analizzando l’intera formula in C9:

=SE(B9=”riempi A”;$C$2;SE(B9=”svuota B”;$C$3;SE(B9=”travasa”;MIN(D8;$C$3-E8);””)))

da leggere come: se l’azione è “riempi A”, allora il liquido da versare è la capacità di A; altrimenti, se è “svuota B”, il liquido da eliminare è pari alla capacità di B; ancora, se l’azione è “travasa”, allora il liquido in gioco è quello contenuto in A, purché B non trabocchi, quindi è il minimo tra il contenuto di A e lo spazio disponibile in B.
Infine, se l’azione non è nessuna di queste, vuol dire che il procedimento è fermo, quindi lascia vuota la cella.

Il contenuto dei recipienti

Terza formula, contenuto di A (D9):

=SE(O(B9=””;B9=”stop”);””;SE(B9=”riempi A”;D8+C9;SE(B9=”travasa”;D8-C9;D8)))

La cella viene lasciata vuota se il procedimento è fermo; altrimenti la quantità D9 viene aggiunta (D8 + C9, “riempi A”) oppure sottratta (D8 – C9, “travasa”). Negli altri casi il contenuto di A rimane invariato (D8).

Analoga la formula per il contenitore B (cella E9):

=SE(O(B9=””;B9=”stop”);””;SE(B9=”svuota B”;0;SE(B9=”travasa”;E8+C9;E8)))

Procedimento “travaso da B ad A”

Nelle colonne da G a J si replica il procedimento invertendo il ruolo tra A e B.
Mutatis mutandis, le formule sono del tutto analoghe. Vediamo, ad esempio quella dell’azione:

=SE(O(G8=”stop”;G8=””);””;SE(O(I8=$C$4;J8=$C$4);”stop”;SE(I8=$C$2;”svuota A”;SE(J8=0;”riempi B”;”travasa”))))

Come si vede “svuota B” e “riempi A” sono state sostituite “svuota A” e “riempi B”. Alcuni parametri sono stati modificati, ma l’impostazione logica delle formule rimane la stessa.

Qualche raffinamento successivo

Mi è capitato spesso di utilizzare per lavoro fogli Excel con un’impostazione creativa come quella del Risolutore presentato in questo post, per automatizzare l’esecuzione di procedimenti ripetitivi, generalmente report statistici.
In questi casi è utile aggiungere qualche automatismo che evidenzi il risultato e per segnalare anomalie.

Per il nostro Risolutore potrebbe tornare utile aggiungere l’indicazione del numero di passi per ciascuno dei due procedimenti e una segnalazione nel caso di mancata terminazione.
Per farlo (foglio “risolutore+”) occorrono un paio di funzioni Excel aggiuntive.

La prima:

=CONFRONTA(“stop”;B:B;0)

trova in quale riga della colonna B si trova “stop”. Il parametro finale 0 indica che si cerca un match esatto.
Per conoscere il numero di passi del procedimento basterà allora calcolare la posizione di “stop” rispetto a quella di “inizio” e sottrarre 1 (perché “stop” non è un passo):

CONFRONTA(“stop”;B:B;0)-CONFRONTA(“inizio”;B:B;0)-1

Cosa succede se il procedimento non si ferma? Succede che la stringa “stop” non viene trovata e la funzione CONFRONTA va in errore (#N/D).
In questo caso interviene la seconda funzione:

= SE.ERRORE(espressione1; espressione2)

che restituisce il valore dell’espressione 1, se questa non va in errore; altrimenti restituisce il valore dell’espressione 2.

Vediamo come si applica al caso del “travaso da A a B” (l’altro è analogo):

=”Travasi da A a B” & SE.ERRORE(” termina in ” & (CONFRONTA(“stop”;B:B;0)-CONFRONTA(“inizio”;B:B;0)-1) & ” passi”;” non termina!”)

Basterà ricordare che il carattere & concatena due stringhe in una, e la formula dovrebbe essere chiara.

Aggiungere ancora intelligenza al foglio Excel è possibile.
Ad esempio si potrebbe distinguere, in caso di mancata terminazione, se ciò è dovuto al numero insufficiente di righe attrezzate, oppure all’impossibilità di trovare una soluzione.
Il foglio “risolutore++” aggiunge questa intelligenza. Come? Scoprirlo è un divertimento lasciato alla curiosità di chi legge!