Cosa ci porterà il nuovo anno? Visti i regali dei suoi recenti predecessori, ci basterebbe un po’ di operosa tranquillità.
Nell’attesa di verificare direttamente, posso replicare il gioco con il quale solitamente attendo il nuovo anno: dare un’occhiata aritmetica al numero 2023, per cominciare a svelare qualcosa del carattere dell’anno che ci attende.
Per cominciare 2023 è un numero dispari, nella simbologia dei numeri viene visto quindi come qualcosa di incompleto, a differenza dei pari a cui si associa la perfezione. Per come è andata con il 2020 (Covid) e il 2022 (invasione dell’Ucraina), darei un po’ di credito ai dispari.
Vediamo altre curiosità legate al 2023.
I numeri del 2023: cominciamo dai fattori primi
2023 è un numero composto. L’ultimo numero primo che abbiamo visto passare è il 2017, il prossimo sarà il 2027. Con l’aiuto di una calcolatrice (sullo smartphone ho questa, bellissima, replica digitale di una Casio scientifica) scopriamo che 2023 = 7 × 17 × 17.
Ora, non voglio lasciarmi guidare dalla scaramanzia legata alla mia origine campana, ma ribadire il 17 mi sembra eccessivo. Verrebbe da dire che partiamo con il piede sbagliato.
Come siamo messi a venerdì 17?
Al 17 è legata la diffidenza verso i venerdì 17. In un articolo di qualche anno fa si era visto che di giornate così in un anno ce n’è sempre almeno una e al massimo tre. Come va con l’anno in arrivo? Il 2023 ce ne porta 3, di più non poteva fare.
Quindi attenzione al 17 di febbraio, marzo e novembre.
I numeri del 2023: la somma delle cifre
Colpisce a prima vista una coincidenza: la somma delle cifre di 2023 è 7, che è anche uno dei suoi fattori primi.
Quanto è comune questo legame tra somma delle cifre e fattori primi? Qualche riga di Python ci aiuta a fare chiarezza.
min_n = 1000
max_n = 3000
for n in range (min_n, max_n+1):
if n%3 == 0:
continue
s = sum([int(k) for k in str(n)])
if n%s == 0:
print (n,s)
Il codice esplora i 2001 anni dal 1000 al 3000 inclusi, alla ricerca di anni con questa proprietà, saltando quelli multipli di 3, per i quali l’evento è molto più probabile.
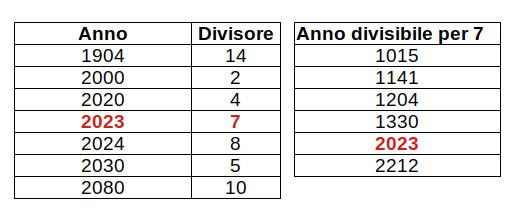
Si trovano 105 ricorrenze, che diventano 363 se si includono i multipli di 3. Ecco un dettaglio di quanto produce il codice:
Questi primi anni del 2000 ci hanno dato un’abbondanza di casi di questo tipo, anche trascurando i multipli di 3: è capitato nel 2000, poi nel 2020 e anche il prossimo anno rientra nella categoria. Ma, prima del 2000, il precedente risaliva al 1904 e, dopo il 2030, occorrerà attendere il 2080.
Se ci si limita ai multipli di 7, vediamo che il precedente risale al 1330 (quando il diciassettenne Boccaccio fantasticava a Napoli per la sua Fiammetta, probabilmente Maria d’Aquino, figlia illegittima di Roberto D’Angiò) e poi occorrerà attendere il 2212 per vederne un altro.
2023 come somma o differenza di potenze
Un’altra curiosità che mi piace esplorare è quella della possibilità di esprimere un numero come somma o differenza di potenze. Venendo al 2023, altre righe di codice Python e si scopre che non c’è modo di esprimere 2023 come somma di potenze di numeri interi positivi, almeno fino all’ottava potenza.
Anche se il 2023 non ce l’ha, questa proprietà è abbastanza comune. L’ultimo caso è stato il 2020 (162 + 422 e 242 + 382), mentre il prossimo sarà il 2025 (272 + 362).
Va meglio se cerchiamo di esprimere 2023 come differenza di quadrati, si trovano infatti tre soluzioni: 682 – 512, 1482 – 1412 e 10122 – 10112.
Non dovrebbe sorprendere osservare che 68 – 51 = 17, 148 – 141 = 7 e 1012 – 1011 = 1. Basta rispolverare qualche ricordo scolastico delle medie, tipo a2 – b2 = (a + b)(a – b).
Il metodo di Fermat per scomporre un numero in fattori primi
Al matematico Pierre de Fermat si deve la famosissima congettura di Fermat, solo da pochi anni dimostrata vera.
Tra i tanti altri risultati prodotti da Fermat, c’è anche un metodo per trovare i fattori primi di un numero composto, basato proprio sulla proprietà appena descritta.
Se, infatti, si riesce a trovare due numeri a e b, tali che N = a2 – b2, allora si può scrivere N = (a + b)(a – b) e quindi (a + b) e (a – b) sono fattori primi di N.
Fermat dimostrò questo metodo trovando i fattori primi di 2027651281, vale a dire 44021 e 46061.
La vicinanza tra i due fattori si traduce in un valore basso per b, e quindi in una buona rapidità dell’algoritmo, il che fa sorgere il dubbio che l’esempio sia stato costruito ad arte per fare marketing del suo metodo. Rimane il fatto che si tratta di un approccio estremamente ingegnoso.
I numeri del 2023: date palindrome
Il 2022 è stato ricco di date palindrome, cioè di date che rimangono invariate se si inverte il senso di lettura dall’ultima cifra dell’anno alla prima del giorno. Esempio: 22-1-22, 22-2-22, …
Non va così bene con il 2023, a causa del 23 che letto al contrario si legge 32. Rimane infatti una sola data palindroma.
Cominciamo con l’osservare che né la stringa 3202023, né la stringa 32022023 si possono dividere in alcun modo per formare una data consistente nel formato esteso gg/mm/aa oppure gg/mm/aaaa.
Bisogna allora ricorrere alla notazione breve: g/m/aa, grazie alla quale venerdì 3 febbraio 2023 (3-2-23) si legge invariato rovesciando il senso di lettura. Ricordiamoci di festeggiare in modo adeguato, visto che solo due venerdì dopo sarà il 17.
I numeri del 2023: aritmetica con le cifre 0, 2, 2 e 3
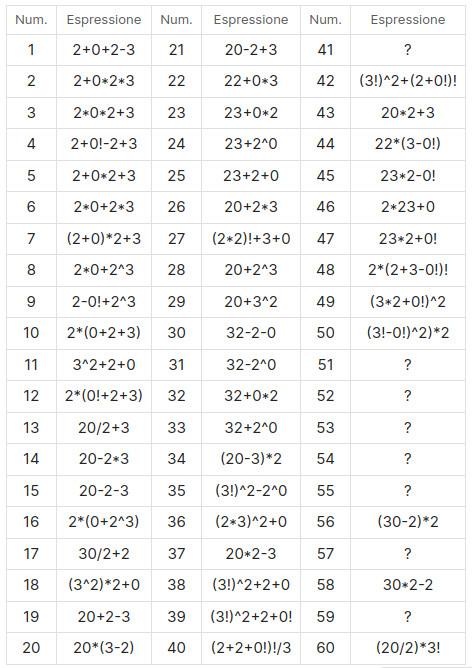
Qualche tempo fa avevo visto su Math.stackexchange.com il post di una persona che chiedeva come esprimere 41 utilizzando una volta sola ciascuna delle cifre di 2023 (quindi due volte il 2 e una volta ciascuno lo 0 e il 3) e delle operazioni scelte tra le quattro operazioni aritmetiche, l’elevamento a potenza e l’operazione di fattoriale (es.: 4! = 1 × 2 × 3 × 4 = 24). Consentito raggruppare le cifre, esempio: 20⁄2 + 3 = 13.
Perché 41? Semplicemente perché era l’unico caso irrisolto, rispetto al suo obiettivo di esprimere in quel modo tutti i numeri da 1 a 50.
La cosa mi aveva intrigato, spingendomi a provare. In poco meno di un’ora sono arrivato esattamente allo stesso punto, tutti i valori da 1 a 50 risolti, tranne il 41.
In realtà, volendo rappresentare le espressioni in una tabella tutta piena, mi sono spinto fino a 60, ma riuscendo a coprire solo tre casi dei numeri da 51 a 60.
Qualche “trucco”
Oltre alle cifre 0, 2 (due volte) e 3, è possibile anche ricorrere a 0! = 1, 3! = 6. E ancora (3 + 0!)! = 24. Ovviamente ricorrere a questi accorgimenti consuma le cifre coinvolte.
Rimane da analizzare in modo esaustivo il caso del 41
Non ne sono venuto a capo manualmente, ma non è detto che non riprovi in un prossimo futuro con un approccio più rigoroso.
Sto meditando infatti di scrivere un generatore di tutte le espressioni possibili, secondo i requisiti del problema.
È complicato, almeno per me, quindi sono in fase di meditazione nel retro-cranio. Per ora mi è venuto in mente che devo comunque porre un limite al numero di operazioni di fattoriale utilizzate. Senza un limite esplicito il generatore potrebbe andare avanti all’infinito. Si pensi, ad esempio, a 3!!! = 260121894356579510020490…000000, per un totale di 1747 cifre.
Nella tabella si vede che ho usato al massimo due operazioni di fattoriale, quindi penso che porre un limite a 3, di cui al massimo 2 consecutivi, sia ragionevole.
2023, pronti… via!
Tradizionalmente accolgo il nuovo anno con un conteggio alla rovescia, realizzato con un’espressione aritmetica che utilizza le cifre da 9 a 0 in ordine decrescente, le 4 operazioni più elevamento a potenza ed eventualmente il fattoriale.
Qualche anno fa calcolai le espressioni di questo tipo per svariati anni a partire dal 1952 (la mia nascita), tra questi è compreso il 2023. Quindi, count down!
987 + 6 + 5 + 4 – 3 + 210 = 2023 !!!
Nota bene, i punti esclamativi esprimono solo entusiasmo, non sono fattoriali!
La foto di apertura è di Tumisu, da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.