Il Goldbach game

Cos’è il Goldbach game?
Tempo fa avevo scritto della Congettura di Goldbach, un tema che mi appassiona fin dai tempi dell’università: “Ogni numero pari maggiore di 2 può essere espresso come somma di due numeri primi“.

La congettura non è un teorema ma, appunto, una congettura, in attesa da quasi 300 anni di una dimostrazione. Per ora ha retto a diversi tentativi di dimostrazione e alla verifica puntuale fino a 4.000.000.000.000.000.000, risultato confortante ma che non può sostituire una prova rigorosa.
Fin da quando ho cominciato a interessarmi alla congettura, ho avuto a portata di mano un’osservazione che mi è sempre sfuggita: il numero di modi in cui un numero pari 2N può essere espresso come somma di due numeri primi, cresce con il numero stesso. Questo porterebbe ad indicare che, per soddisfare la congettura per tutti i pari fino a 2N, potrebbe essere sufficiente una quantità di numeri primi ridotta, rispetto a quella disponibile.

Qualche tempo fa, in risposta al mio articolo, ho ricevuto una email da Vittorio Ornago, appassionato come me di matematica ricreativa e, in particolare, della congettura di Goldbach. Grazie a una notevolissima abilità di calcolo, Vittorio sta costruendo gli insiemi minimi di numeri primi sufficienti a verificare la congettura per i valori di 2N fino a 200. Impresa assolutamente non banale. A questa sfida personale Vittorio ha dato il nome di Goldbach game.

Il Goldbach game: un esempio per cominciare

Partiamo, per chiarirci le idee, da un valore di 2N = 24. La tabella che segue mostra le possibili combinazioni dei primi minori di 24, rappresentabili con l’insieme [3, 5, 7, 11, 13 17, 19, 23] (manca il 2, per un motivo chiarito nel seguito):

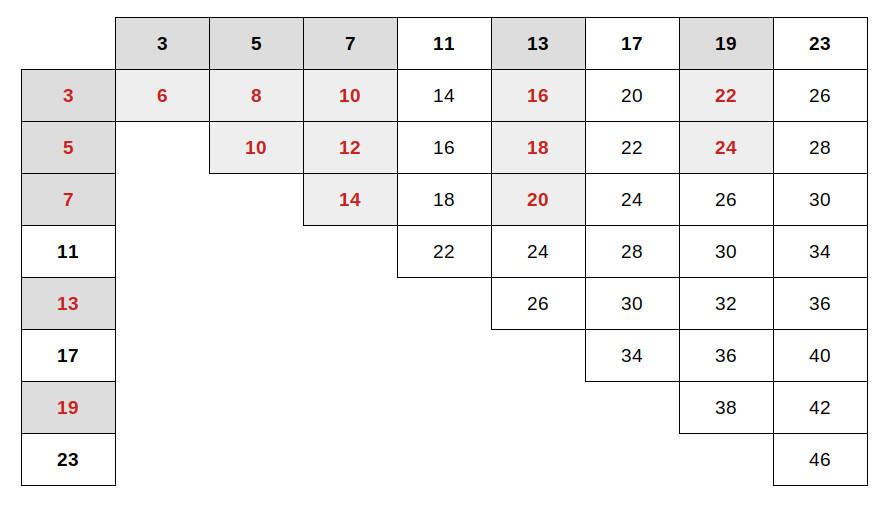L’immagine evidenzia in rosso su sfondo grigio le combinazioni possibili utilizzando solo la selezione di primi [3, 5, 7, 13, 19], ignorando 11, 17 e 23.
Una vista diversa del numero di combinazioni possibili può aiutare a capire l’effetto della selezione:

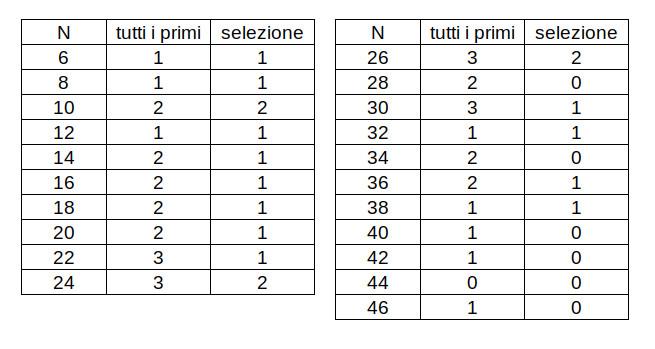È evidente come, utilizzando tutti i primi disponibili, ci sia una ricchezza di possibilità di comporre 2N (colonna tutti i primi) e che è possibile comporre numeri pari anche di molto superiori a 2N (tabella di destra).
Utilizzando la selezione di primi, invece, si riduce l’eccesso di combinazioni possibili, pur rispettando l’esistenza di almeno una combinazione per ogni numero pari fino a 24.

Di quanto si riduce al crescere di 2N la quantità di numeri primi sufficienti a verificare la congettura?

Questa è la prima domanda che mi ha posto Vittorio.
Con un algoritmo consistente nel taglio di sottoinsiemi di primi della forma ax + b, con a e b fissi e x variabile, Vittorio è riuscito a tagliare i 2/3 dei primi disponibili, verificando la congettura per valori di 2N fino a 2 miliardi. Qual è, in effetti, a tendere, la frazione di primi necessaria?

Un approccio esaustivo e un algoritmo euristico

È evidente che una risposta rigorosa a questa domanda richiederebbe di avere prima dimostrato la validità della congettura per tutti i numeri pari. Quindi, allo stato delle cose, è possibile fornire una risposta solo nell’ambito di valori limitati di 2N.
Ancora, si possono assumere due approcci:

una ricerca esaustiva dei sottoinsiemi di primi ottimali;
un algoritmo euristico che determini sottoinsiemi ridotti ma non necessariamente ottimali.

Il secondo approccio consente di arrivare molto avanti nella ricerca, ma ovviamente fornisce una risposta migliorabile con il primo approccio.

Una premessa, prima di aprire il Goldbach game

Il più piccolo numero primo è 2, ovviamente l’unico pari. Nella verifica della congettura, 2 serve solo ad esprimere 4 come 2 + 2. Combinandosi con qualunque altro primo, necessariamente dispari, darebbe infatti come somma un numero dispari. È questo il motivo per cui non ho incluso il 2 nella tabella riportata in precedenza.
Il pari successivo, 6, può esprimersi solo come 3 + 3, quindi anche 3 è necessario in qualunque sottoinsieme di primi che soddisfi la congettura.
Analogamente 8 = 3 + 5 richiede l’inserimento di 5, cosa che soddisfa anche 10 = 5 + 5. Ma 12 = 5 + 7 porta a inserire come socio fondatore anche il 7, che basta anche per 14 = 7 + 7.

Con il 16 comincia il gioco vero e proprio, perché 16 = 3 + 13, ma anche 16 = 5 + 11. Quale primo inserire, quindi: 11 o 13?

L’approccio euristico

Sono partito, Python alla mano, con l’algoritmo euristico.
A partire dal sottoinsieme minimo [2, 3, 5, 7] e da 2N = 16:

se esiste nel sottoinsieme una coppia di primi che dà come somma 2N, procedo con il pari successivo;
altrimenti inserisco nel sottoinsieme il massimo primo disponibile che consente di soddisfare la congettura.

Per 2N = 16 i primi disponibili e non ancora utilizzati sono 11 e 13, quindi scelgo 13. e il sottoinsieme diventa [2, 3, 5, 7, 13].

Perché inserire il massimo primo disponibile e non, ad esempio, il minimo?
Serve un criterio di selezione semplice, e scegliere il massimo dovrebbe fornire più possibilità di combinazione al crescere di 2N. In effetti qualche verifica suggerisce che sia proprio così, ma il ragionamento è, per l’appunto, euristico o, per meglio dire, di buonsenso.

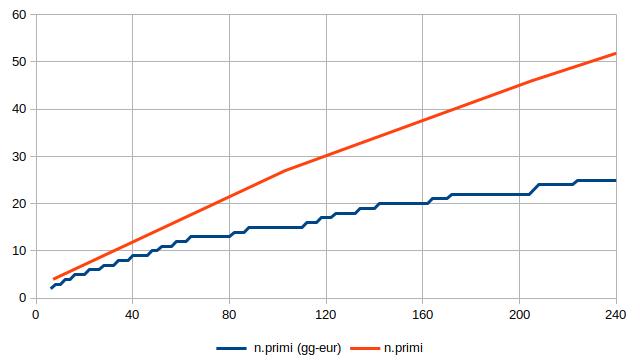
Il grafico che segue mostra il numero di primi disponibili (linea rossa) e la dimensione del sottoinsieme via via costruito (linea blu), per valori di 2N minori di 10.000. È evidente che la frazione di primi utilizzati tende a valori decisamente più bassi di 1/3:

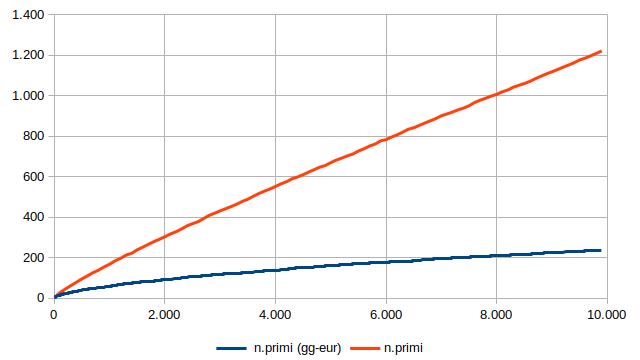Quanto più bassi?

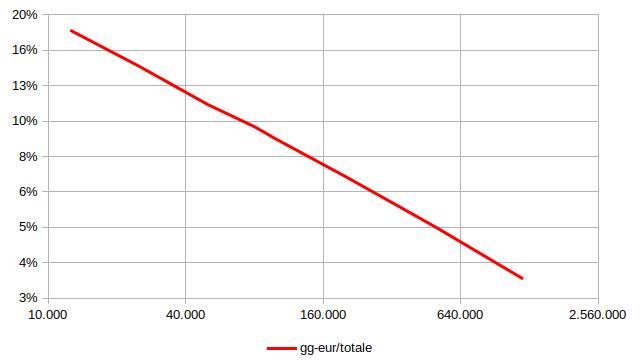
Per valori di 2N più alti conviene utilizzare scale logaritmiche per gli assi:

La percentuale di primi utilizzati scende al di sotto del 4% per 2N = 1.280.000.
Come si comporterà la curva per valori di 2N ancora maggiori? Si stabilizzerà su un valore, per quanto basso, o tenderà a zero? I tempi di elaborazione della mia implementazione dell’algoritmo sono decisamente lunghi per spingersi oltre, ma, dovessi scommettere, punterei su un limite tendente a zero.

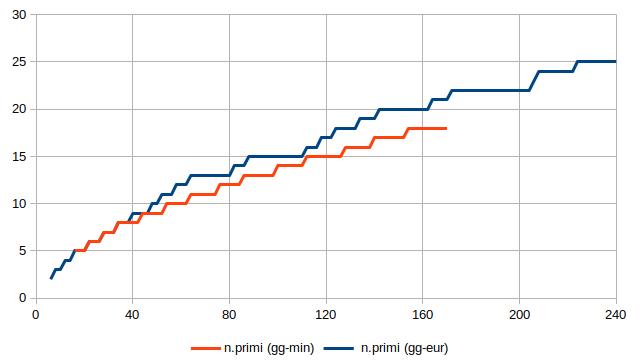
E, a proposito dell’algoritmo, un dettaglio. Una volta aggiunto un nuovo primo al sottoinsieme, non procede direttamente con il 2N successivo, ma calcola la copertura del sottoinsieme, cioè il valore di 2N fino al quale quel sottoinsieme soddisfa la congettura, e riparte dal successivo.
Il grafico che segue, che evidenzia l’andamento a scalini della curva blu per bassi valori di 2N, dovrebbe rendere meglio l’idea:

Goldbach game: un approccio esaustivo

Un algoritmo esaustivo per determinare il minimo numero di primi necessari a soddisfare la congettura fino a un numero pari dato 2N può essere costruito in questo modo:

costruisco l’insieme dei primi minori di 2N (P = [2, 3, 5, 7, …, p]);
assumo che la congettura sia verificata dall’insieme P per tutti i pari fino a 2N, quindi il numero minimo iniziale L è pari al numero di elementi in P;
analizzo uno per uno i sottoinsiemi S_P di P;
se S_P ha un numero di elementi uguale o maggiore di L, passo al sottoinsieme successivo;
altrimenti verifico se S_P soddisfa la congettura per tutti i pari fino a 2N; in questo caso aggiorno il valore di L.

Una volta esauriti i sottoinsiemi di P, in L troverò il numero minimo di primi cercato.

I tempi di elaborazione di un algoritmo del genere crescono esponenzialmente con il numero di primi minori di 2N.
Il numero di sottoinsiemi di un insieme P dato con L elementi, infatti, è pari a 2^L. Come ci si arriva? Basta pensare che ogni numero da 0 a 2^L – 1 può essere rappresentato da una stringa di L cifre binarie 0 o 1, che a sua volta può essere associata a un diverso sottoinsieme di P, dove l’elemento corrispondente di P è presente (cifra 1) o assente (cifra 0).

Per concludere, sul Goldbach game

Nonostante diverse ottimizzazioni, la crescita del tempo di esecuzione di questo algoritmo consente di determinare il minimo numero cercato solo per valori molto bassi di 2N. Pur con questo limite appare però evidente che l’algoritmo euristico fornisce una risposta generosamente abbondante rispetto al valore reale:

La verifica esaustiva si è fermata infatti a 2N = 170. A fronte di 39 primi minori di 170, l’algoritmo esaustivo fornisce un numero minimo di 18 primi:

[2, 3, 5, 7, 13, 19, 23, 31, 37, 41, 43, 47, 53, 79, 101, 109, 113, 127],

mentre per l’algoritmo euristico sono necessari 21 primi:

[2, 3, 5, 7, 13, 19, 23, 31, 37, 43, 47, 53, 61, 79, 83, 101, 109, 113, 131, 139, 157].

Per adesso la mia ricerca si è fermata qui, in attesa di una illuminazione che mi consenta una ricerca esaustiva che si spinga oltre. Arriverà quando meno me l’aspetto?

Foto di apertura di tigerlily713 da Pixabay.