Una domanda posta di recente su Math.stackexchange.com propone un problema che offre lo spunto per rispolverare un argomento finito (per me) nel dimenticatoio: i grafi; l’articolo è Broken calculator puzzle (ways to reach a desired number using a restricted list of operations).
Il problema posto si riassume semplicemente: si supponga di partire dal numero 2 e voler raggiungere il numero 1.000, avendo a disposizione solo due tipi di operazione. Quanti percorsi diversi sono possibili? Le due operazioni a disposizione sono l’incremento di 1 ( es.: 2 → 3) e l’elevazione al quadrato (es.: 3 → 9).
Altra domanda possibile: qual è il percorso più breve?
Per rispondere a queste domande una strada possibile è quella di rappresentare il problema con dei grafi.
Cosa sono i grafi
Un grafo è una struttura matematica costituita da nodi (o vertici) e collegamenti tra i nodi o vertici. Un esempio classico di grafo è quello che rappresenta il problema dei ponti di Königsberg (se ne era scritto qui): il grande matematico e fisico svizzero Eulero si era chiesto se fosse possibile una passeggiata tra i ponti della città di Königsberg, posti alla confluenza nel fiume Pregel dei suoi affluenti, percorrendoli tutti, ma ognuno solo una volta.
La risposta è che non è possibile farlo ma, come spesso accade in matematica, si arrivò a questo no grazie a una nuova, preziosa teoria matematica, quella appunto dei grafi.
È uno dei meccanismi vincenti della matematica: creare un modello, e analizzare le proprietà e gli algoritmi che si possono applicare al modello, consente poi di utilizzare proprietà e algoritmi per le situazioni di vita reale che possono riportarsi a quel modello.
I grafi per il problema dei percorsi da 2 a 1000
Affrontare un problema di petto si rivela spesso un approccio infruttuoso. Può essere molto più efficace partire da un problema che abbia la stessa struttura di quello dato, ma una dimensione ridotta, più facile da visualizzare e da analizzare.
Invece di affrontare subito il caso Da 2 a 1.000, partiamo da un caso molto più semplice: Da 2 a 4, sempre con la limitazione di avere a disposizione solo le due operazioni di incremento di 1 e di elevazione al quadrato.
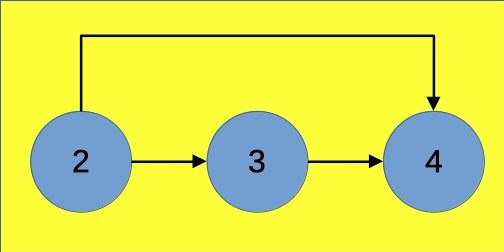
Rappresentando i numeri con dei nodi e le operazioni come dei collegamenti tra i nodi, il problema si traduce così:
Il grafo è un grafo orientato, perché i collegamenti portano da un nodo di partenza a uno di arrivo e non sono percorribili in senso opposto.
In questo semplice caso i percorsi possibili sono due:
- 2 → 3 → 4;
- 2→ 4.
Nel primo caso si sono effettuati due incrementi di 1, nel secondo un’elevazione al quadrato.
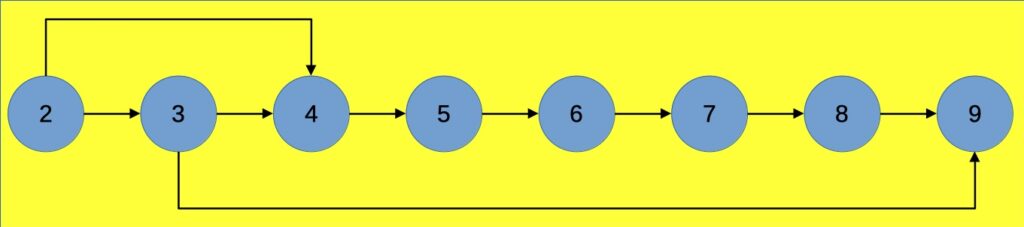
Questo primo esempio non ci dice molto per il problema originario, dobbiamo complicare un po’ la situazione, spingendoci fino a 9, quadrato di 3:
I percorsi possibili diventano 3:
- 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9;
- 2→ 4 → 5 → 6 → 7 → 8 → 9;
- 2 → 3 → 9.
Già questa prima complicazione offre almeno un paio di spunti utili alla soluzione.
Il primo è che l’incremento di percorsi possibili nasce con i nodi che sono un quadrato perfetto. Se, infatti, ci si fosse fermati a 8, i percorsi sarebbero rimasti solo 2.
Leggibilità dei grafi
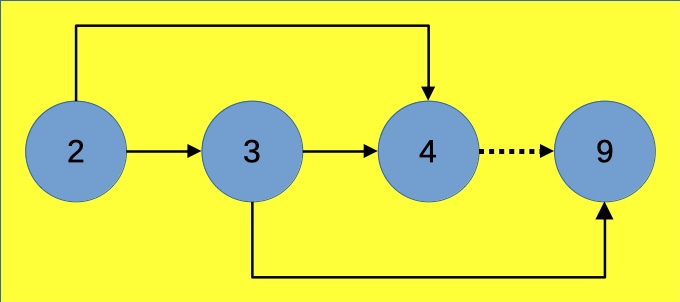
Il secondo è che si può, ed è conveniente, rendere un po’ più compatta la rappresentazione grafica, senza nulla togliere alla rappresentatività del grafo:
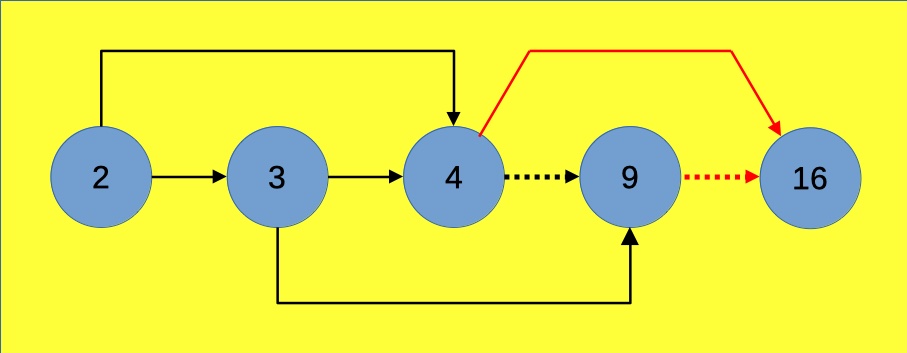
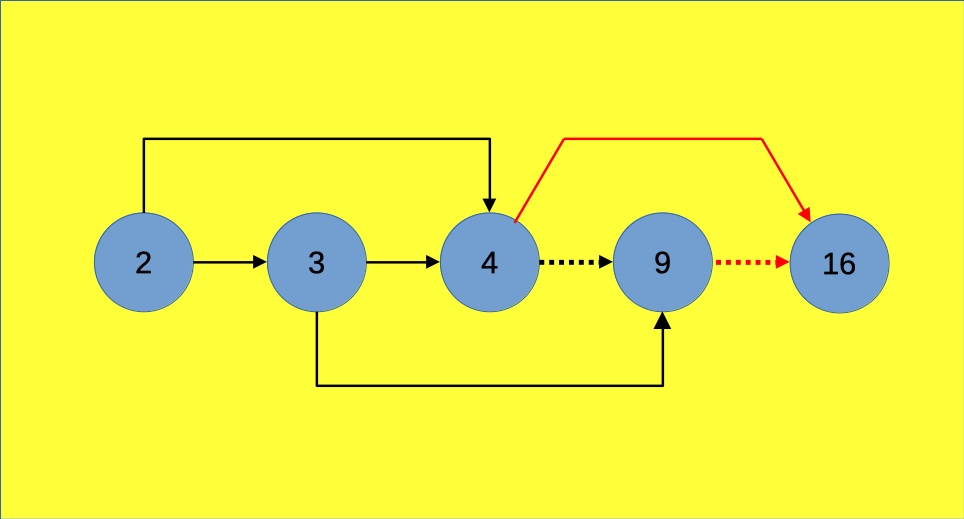
Per cominciare a trarre qualche conclusione occorre quindi spingersi fino al successivo quadrato, 16:
Ancora una volta va sottolineato che il numero di percorsi possibili, quando ci si fermi a 15, rimane quello visto per il caso con traguardo fissato a 9. È l’aggiunta del quadrato perfetto 16 che porta nuovi percorsi.
Quali? La linea punteggiata rossa semplicemente prolunga fino al 16 i percorsi giunti al 9. La linea continua rossa, invece, offre ai percorsi arrivati al 4 un finale diverso, saltando subito al 16.
Quindi, se indichiamo con P(n) il numero dei percorsi diversi che arrivano a n, possiamo scrivere che:
- P(16) = P(9) + P(√16).
Dai grafi alla regola di calcolo
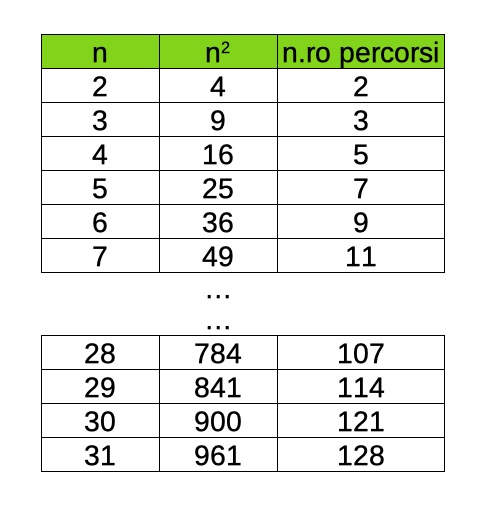
È il momento di trarre le conclusioni. Da quanto si è visto sarà sufficiente costruire una tabella del numero dei percorsi che portano da 2 a n2, con n che va da 2 a 31, il più grande numero il cui quadrato (961) è minore di 1.000.
La tabella può essere costruita progressivamente, sapendo che P(4) = 2 e P(9) = 3. Si proseguirà quindi con P(16) = P(9) + P(4) = 3 + 2 = 5 e, a seguire, P(25) = P(16) + P(5) = P(16) + P(4) = 5 + 2 = 7.
Il tutto si può agevolmente realizzare con un foglio di calcolo (LibreOffice Calc o Excel), con poche semplici formule.
Nella prima colonna (colonna B) ho inserito i numeri progressivi da 2 a 31, nella seconda (Colonna C) il quadrato della corrispondente cella della colonna B.
Nella terza cella (colonna D) ho posto la formula che calcola il corrispondente numero di percorsi nel grafo.
Esempio, se in B6 c’è il valore 5, in C6 c’è 5 * 5 = 25, e nella cella D6 c’è la formula:
-
=CERCA.VERT(INT(RADQ(B6))^2;$C$2:D5;2;0)+D5.
Tradotto in linguaggio (spero) comprensibile, la formula determina il nodo (INT(RADQ(B6))^2) a cui si riporta la gamba addizionale del nuovo nodo e ne cerca il numero di percorsi nella tabella $C$2:D5.
Le formule sono poi copiate per trascinamento, fino alla riga 32, che ci fornisce la risposta cercata: i percorsi diversi tra loro che portano da 2 a a 961 (e quindi da 2 a 1.000) sono in tutto 128.
Nell’articolo di Math.stackexchange.com citato in apertura ci sono almeno un altro paio di approcci che portano al risultato.
E il percorso più breve?
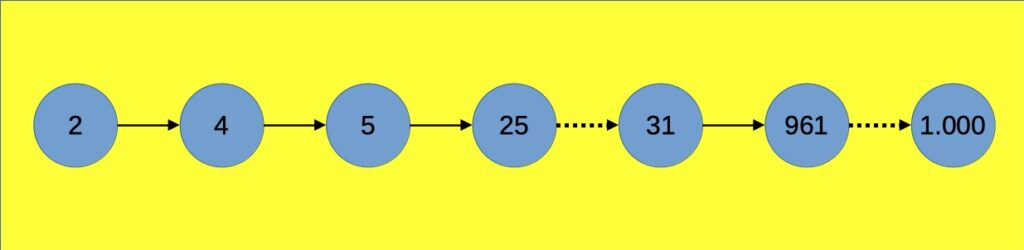
Il percorso più breve può essere intuitivamente costruito a ritroso, partendo da 1.000 e proseguendo fino al primo quadrato che si incontra, che, come visto, è 961, quadrato di 31. Perché il primo che si incontra? Semplicemente perché è quello che consentirà il massimo salto a ritroso.
Il passo successivo, ancora da gambero, è quindi un salto da 961 a 31, e da qui, sempre all’indietro, fino al prossimo quadrato, 25.
Altro salto, da 25 a 5, e da qui a 4 e, infine, a 2.
Il tutto come schematizzato dal grafo che segue:
Il numero di passi per questo percorso sarà quindi: 1 + 1 + 1 + 6 + 1 + 39 = 49 passi, di cui 46 incrementi di 1 e 3 elevazioni al quadrato.
Articoli correlati:
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
