Terne pitagoriche: come ricercarle con Ruby e script Bash

Alle terne pitagoriche ho dedicato nel tempo diverse ore del mio tempo libero, frugando tra le mille curiosità matematiche racchiuse nei triangoli rettangoli con lati misurati da numeri interi. Generalmente la sfida implica l’analisi di lunghe sequenze di numeri con molte cifre e, quindi, richiede uno sforzo di fantasia e creatività nel pensare e realizzare gli algoritmi necessari.
Molti anni fa, correva il 1984 (o forse il 1985), il mio capo di allora in Olivetti mi propose un problema a cui stava lavorando, proprio relativo alle terne pitagoriche. Ecco la ricostruzione di quell’avventura.

Cosa sono le terne pitagoriche

Chi non ricorda che “In ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati costruiti sui cateti“? Esatto, è l’enunciato del buon vecchio teorema di Pitagora.
Bene, quando le misure dei cateti e quella dell’ipotenusa sono numeri interi, allora siamo di fronte a una terna pitagorica. Il triangolo in questione è invece identificato come triangolo pitagorico.

La più nota delle terne pitagoriche è (3,4,5), che individua un triangolo rettangolo con cateti che misurano rispettivamente 3 e 4, mentre l’ipotenusa misura 5. E infatti è: 3² + 4² = 5².

Le terne pitagoriche sono legate all’Ultimo teorema di Fermat, congettura del 1637 dimostrata vera dal matematico Andrew Wiles nel 1994: l’equazione xⁿ + yⁿ = zⁿ ha soluzione con x, y e z interi e maggiori di zero solo per n=2. In questo caso le soluzioni sono le infinite terne pitagoriche.

Le terne pitagoriche nella storia

Già gli antichi geometri egizi conoscevano la terna (3,4,5) che utilizzavano per tracciare precisi angoli retti sul terreno.
Per farlo, infatti, ricorrevano a una corda richiusa agli estremi, con 12 nodi posti a distanza di una unità l’uno dall’altro. Tendendo la corda in tre punti particolari, potevano così formare un triangolo rettangolo con lati lunghi rispettivamente 3, 4 e 5 unità. L’angolo tra il lato da 3 e quello da 4 era quindi retto.

Il teorema di Pitagora era peraltro noto già ai Babilonesi. La tavoletta Plimpton 322, risalente al 1800 a.C., annota infatti una tabella di alcune terne di lati di triangoli rettangoli, utili probabilmente nell’esecuzione di calcoli astronomici.

Una formula generale per generare tutte le infinite terne pitagoriche si deve a Euclide, attivo intorno al 300 a.C.

Il problema dei triangoli pitagorici di uguale area

Non ricordo esattamente quando il mio capo di allora in Olivetti, F.L., mi propose un problema a cui stava lavorando nel tempo libero: trovare un insieme di più di tre triangoli pitagorici di uguale area. Siamo comunque tra il 1984 e il 1985.

Programmando con i mezzi di allora, era infatti riuscito a trovare una terna di triangoli di uguale area (840):

(40,42,58)
(24,70,74)
(15,112,113)

Per dare un minimo di contesto: non c’era ancora Google, né peraltro il Web, così come non esisteva ancora il computer personale, non c’era ancora Excel, la potenza di calcolo disponibile era, per usare un eufemismo, molto contenuta. Era quindi complicato raggiungere qualche risultato apprezzabile nelle proprie ricerche amatoriali e, magari, lavorando a qualcosa che era già stato abbondantemente esplorato da altri.

Una semplice ricerca con Google ci dice, oggi, che esistono quaterne, cinquine, … di triangoli pitagorici di uguale area. Nell’Enciclopedia online dei numeri interi la sequenza di aree in questione è identificata con A055193:

6, 210, 840, 341880, 71831760, 64648584000, 2216650756320, 22861058133513600

Sono infatti le aree del più piccolo triangolo pitagorico (6), della prima coppia di uguale area (210), della prima terna (840), della prima quaterna (341.880) e così via.

Non lo sapevamo, quindi, ma la risposta al problema era 341.880, fuori dal raggio di azione del programma messo a punto fino a quel momento.

L’approccio efficientista

Per lo sviluppo ed esecuzione di programmi, in mancanza di computer personali si poteva ricorrere alle ore notturne di un Olivetti P6060 in dotazione all’ufficio.

Macchina assolutamente fantastica, il P6060 aveva un efficientissimo Basic. Unica pecca: la stampa su carta termica ha fatto sì che non conservi nulla dei lavori fatti in quegli anni, a meno di appunti e qualcosa di fotocopiato (pochissimo, e nemmeno so più dov’è, dopo il trasloco di tre anni fa).

Il primo passo da effettuare era quello di ottimizzare l’algoritmo di ricerca, in modo da consentire risultati apprezzabili in meno di 12 ore.

La struttura del programma messo a punto era molto semplice:

formula generatrice di Euclide: cateti m² – n² e 2mn, ipotenusa m² + n²;
produzione di una lista di terne, annotate insieme all’area del triangolo relativo mn(m²-n²);
ordinamento crescente delle terne, in base all’area;
ricerca di eventuali sequenze di più di tre triangoli con la stessa area.

Niente di rigoroso, tutto all’insegna della speraindio.

Il programma in versione moderna

La generazione delle terne è molto semplice. Riscritta in Ruby, viene una cosa così:

nmax, mmax = 100,100
lista = File.new("terne-short.csv","w")
#
lista.write("s,a,b,c,m,n\n")
(1..nmax).each do |n|
	((n+1)..mmax).each do |m|
		a = m**2 - n**2
		b = 2*n*m
		c = m**2 + n**2
		s = a*b/2
		lista.write("#{s},#{a},#{b},#{c},#{m},#{n}\n")
	end
end
lista.close

Utilizzando 100 come limite massimo per m e n, si generano 4.950 terne. Il file dei dati viene memorizzato (oggi) con l’estensione .csv, in modo da poter essere dato in pasto a Excel o, meglio, a Libre Office.

L’ordinamento delle terne

Come detto più su, Excel non c’era ancora, sarebbe arrivato solo nel 1985 per i sistemi Macintosh e nel 1987 per Windows. E dubito che comunque in quegli anni avrebbe avuto la forza per gestire in un tempo ragionevole l’ordinamento di 4.950 record. Gioco forza, quindi, scrivere codice anche per ordinare la lista.

Data la mia lacunosa cultura informatica di allora, ricorsi a uno dei più scarsi algoritmi di ordinamento esistenti: il Bubble Sorting, che però si presta ad essere codificato con poco sforzo. L’avevo trovato tra gli esercizi di programmazione (in assembler!) del processore Zilog Z80.

In sostanza si scorre la lista da ordinare in una direzione (es.: dal fondo risalendo all’inizio), confrontando a due a due gli elementi contigui. Se non sono in ordine, si scambiano di posto.
Il nome di “bubble“, bolla, deriva dal fatto che, supponendo di partire dal fondo, l’elemento più piccolo prevale ad ogni scambio e quindi risale velocemente, come se si trattasse di una bolla d’aria in un liquido.
Per contro, l’elemento maggiore della lista può scendere solo di una posizione ad ogni passaggio. Da qui l’inefficienza dell’algoritmo, se confrontato con altri più complessi, come l’Heapsort, di cui però all’epoca ignoravo anche l’esistenza.

Il Bubble Sorting era però troppo lento, in una notte il mio programma metteva in ordine molto meno di quanto avrebbe dovuto. E al mattino il P6060 serviva ad altri scopi.

Pensa che ti ripensa, si accende la lampadina

In realtà, con una semplice modifica, si poteva velocizzare l’ordinamento. Bastava ricorrere a una scansione alternata: un passaggio dal fondo in cima (facendo risalire l’elemento più piccolo non ancora a posto) e la successiva dalla cima al fondo (facendo scendere l’elemento maggiore tra quelli ancora da sistemare).
Altra ottimizzazione: il programma poteva annotare l’ultima posizione scambiata in entrambi i sensi. Alla passata successiva sarebbe stato inutile proseguire con i confronti oltre quel punto.

Sembrerà banale, ma sono ancora orgoglioso di quelle due pensate.

La prima quaterna!

L’ottimizzazione fu sufficiente a raggiungere lo scopo. Al mattino successivo il programma evidenziava la quaterna di triangoli:

(1320,518,1418)
(280,2442,2458)
(231,2960,2969)
(111,6160,6161)

Tutti con la stessa area pari a 341.880. E, sorpresa, anche una seconda quaterna, di area maggiore!

Come si affronterebbe oggi questa analisi

Nel frattempo è nato Unix, di cui è semplice scaricare una distribuzione, ad esempio Ubuntu, su un pc, anche se scalcagnato. Oppure, ancora meglio, si può attivare il BASH Ubuntu all’interno di Windows 10, con il vantaggio di avere tutto quello che serve in un solo pc.

Ordinare righe, filtrare, eseguire semplici calcoli è il pane di Unix. Ecco, ad esempio, come ottenere, dal file prodotto dal programma Ruby precedente, la lista ordinata delle aree dei triangoli pitagorici con la relativa numerosità. Premessa: ho spezzettato il comando, che invece va tutto su una riga, per poterne descrivere la logica. Inoltre il carattere pipe (“|”) porta i dati prodotti dal comando che precede il pipe a quello che lo segue.

tail -n+2 terne-short.csv |
awk -F "," '{print $1}' | 
sort -g | 
uniq -c | 
awk '$1=$1' | 
awk 'BEGIN { FS=" "; OFS=","; print "s","occorrenze"} { print $2,$1}' | 
sort -t ',' -gk2,2r -gk1,1 > 
terne-short-conta.csv

Raccontato a parole:

prendi le linee del file “terne-short.csv“, a partire dalla seconda (scartando quindi l’intestazione);
isola la prima colonna del file csv ($1);
disponi i dati numerici della colonna in ordine crescente;
estrai i valori unici; a ognuno viene anteposto il numero delle sue occorrenze nella colonna;
elimina gli spazi iniziali e finali;
trasforma i separatori del file da spazi a virgole, scambia la posizione tra valori unici e occorrenze;
ordina i dati, per numero di occorrenze decrescenti e valori crescenti;
scrivi (finalmente) nel file “terne-short-conta.csv“

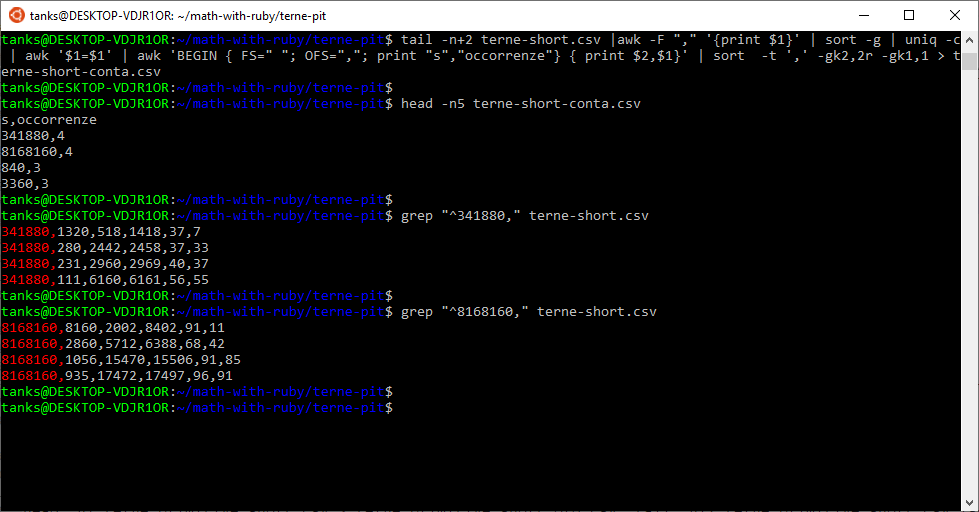
A questo punto è possibile estrarre le prime posizioni della lista e successivamente, dal file “terne-short.csv“, le terne che interessano. La schermata che segue mostra il tutto. Di ogni triangolo viene riportato l’area, i tre lati e i valori generatori della terna, m ed n.

E la prima cinquina?

L’appetito, si sa, vien mangiando. Trovata la quaterna era naturale pensare al passo successivo: cinque triangoli pitagorici di uguale area.

Oggi so che l’area da cercare è pari a 71.831.760, ben al di là di 341.880. E infatti i primi tentativi di spingersi più in là, stiracchiando i limiti del programma e ripulendo il codice per renderlo più efficiente, non raggiunsero lo scopo.
Serviva un approccio diverso.

Le terne pitagoriche primitive

Se i tre numeri di una terna pitagorica non hanno un divisore comune, allora la terna si definisce primitiva. Nella nostra quaterna le prime due terne non sono primitive, poiché ciascuna è il doppio di una terna primitiva. Le ultime due sono primitive.

La prima terna, ad esempio, (1320,518,1418), ha i lati doppi rispetto alla terna primitiva (660,259,709).

Componente quadrata e parte residua

Ora, posso esprimere l’area di una terna primitiva separando i fattori “quadrati” dai fattori con esponente 1. Esempio, se l’area fosse pari a 40 = 2³ * 5, potrei scrivere anche: 40 = (2)² * (2*5) = q² * r,
dove q = 2 e r = 10.

Tutte le terne multiple di questa terna primitiva avranno una componente q maggiore (perché se moltiplico per un fattore k i lati di una terna, l’area viene moltiplicata per k²), ma avranno la stessa componente r.
In altre parole, r (che chiamai parte residua) è una caratteristica che accomuna una terna primitiva e tutti i suoi multipli.

Se quindi ho due terne primitive distinte che abbiano identica parte residua r, con l’area dei rispettivi triangoli pari rispettivamente a q₁² * r e q₂² * r, allora il multiplo q₂ del primo e il multiplo q₁ del secondo hanno la stessa area (q₁ * q₂)² * r.

Bingo! Posso quindi selezionare solo le terne primitive, cercarne 5 o più con la stessa parte residua, e da qui costruire la cinquina (o quello che sarà) di terne cercate. Basterà trovare il minimo comune multiplo delle componenti quadrate e usarlo per scalare le terne primitive di partenza.

La ricerca delle terne pitagoriche primitive

Il programma per generare terne pitagoriche primitive è un po’ più complesso del precedente, poiché, vanno selezionate le coppie di valori generatori m e n che siano primi tra loro e non entrambi pari o entrambi dispari. Sono infatti queste le due condizioni che portano a terne pitagoriche primitive.

Inoltre il valore dell’area va scomposto nella componente quadrata e nella parte residua. Il tempo di esecuzione quindi si allunga, a parità di valori massimi di n e n.

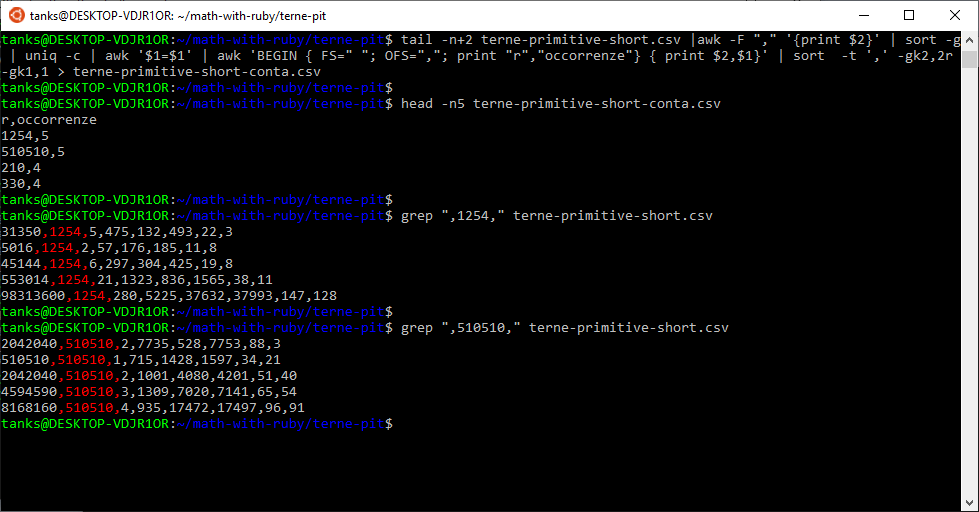
Da qui si può scaricare la versione Ruby del programma, di cui la schermata che segue, analoga alla schermata precedente, mostra i risultati. Impostando il limite di 150 per m ed n si ottengono 4.583 terne primitive.

Due cinquine!
Il primo valore di ogni riga è l’area del triangolo. Evidenziate in rosso sono le parti residue cercate (1254 e 510510). Seguono poi la componente quadrata, le misure dei cateti e dell’ipotenusa e i valori generatori m ed n.

Basta ora trovare il minimo comune multiplo delle componenti quadrate di ogni gruppo (5, 2, 6, 21, 280 –> 840) e (2, 1, 2, 3, 4 –> 12).
L’area della primi cinquina sarà quindi data da 1254 * 840² = 884.822.400. Per la seconda cinquina: 5105150 * 12² = 73.513.440.

La più piccola cinquina è la seconda, che oggi so non essere la minima possibile, di area 71.831.760, come visto. Ma l’obiettivo di trovare una cinquina era raggiunto!

Alla ricerca della cinquina minima ed oltre

In possesso di altri mezzi e conoscendo il risultato, oggi è possibile approfondire la questione.

Partiamo dal calcolare il valore della parte residua r di 71.831.760, che è il valore da trovare.
Ora è:

71.831.760 = (4 * 13)² * 3 * 5 * 7 * 11 * 23 = 52² * 26.565.

E per il valore successivo da trovare? Sempre secondo l’Enciclopedia online l’area della più piccola sestina è:

64.648.584.000 = (8 * 3* 5 * 13)² * 3* 5 * 7 * 11 * 23

Quindi anche qui la parte residua è pari a 26.565.
Un primo dato confortante è che nella nostra lista questo valore di r c’è, anche se solo con tre terne. Evidentemente va estesa l’esplorazione.

Oggi si può

Proviamo a modificare i limiti per m e n, portandoli da 150 a 1000, e modificando nel nome del file-elenco “short” in “large”.
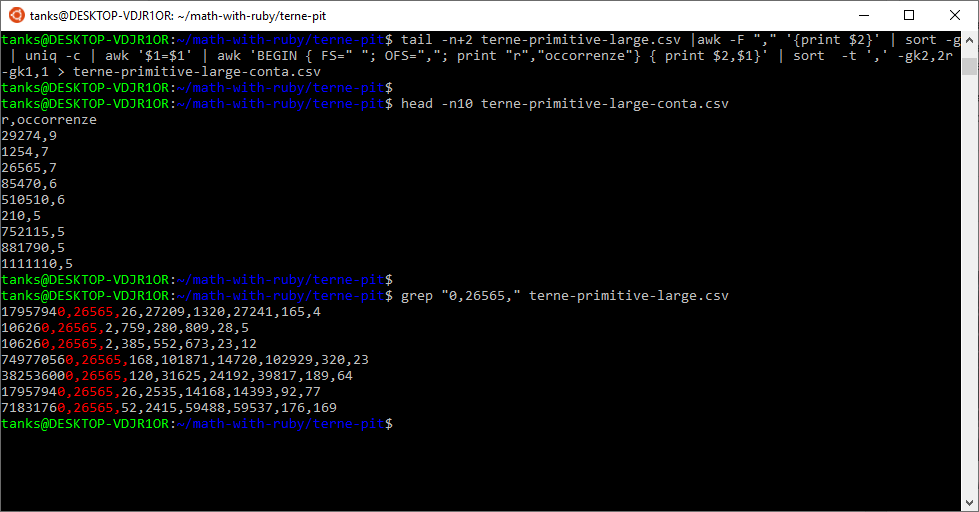
Rieseguendo il programma si ottengono 499.501 terne. Cosa troviamo?

Abbiamo un gruppo di 9 triangoli e due da 7, uno dei quali ha r = 26.565. I relativi 7 triangoli pitagorici sono descritti così (evidenziano in grassetto la parte residua):

17957940,26565,26,27209,1320,27241,165,4
106260,26565,2,759,280,809,28,5
106260,26565,2,385,552,673,23,12
749770560,26565,168,101871,14720,102929,320,23
382536000,26565,120,31625,24192,39817,189,64
17957940,26565,26,2535,14168,14393,92,77
71831760,26565,52,2415,59488,59537,176,169

Per trovare la più piccola cinquina conviene selezionare le prime tre e le ultime due. Il minimo comune multiplo delle parti residue è pari a: (26, 2, 2, 26, 52 –> 52).
Quindi l’area comune ai 5 triangoli cercati è pari a: 26565 * 52² = 71.831.760, che è il valore cercato.

Per la più piccola sestina ricavabile da questo gruppo conviene scartare la quarta riga, ottenendo:
(26, 2, 2, 120, 26, 52 –> 1560), quindi r = 1.560 e l’area dei 6 triangoli risulta uguale a 26565 * 1560² = 64.648.584.000. E anche questo valore torna!

Insieme all’algoritmo di “selezione equiprobabile di un elemento in un gruppo di campioni” descritto nell’articolo precedente, questo elaborato per la ricerca delle terne pitagoriche mi ricorda la meglio gioventù. Prima o poi metterò insieme un libro di ricordi.

Un viaggio tra le terne pitagoriche