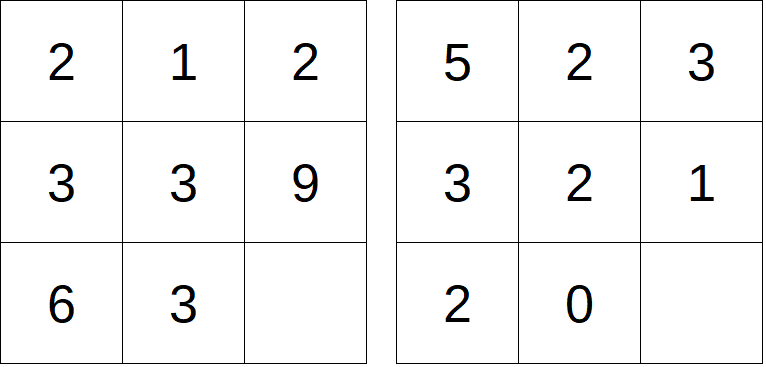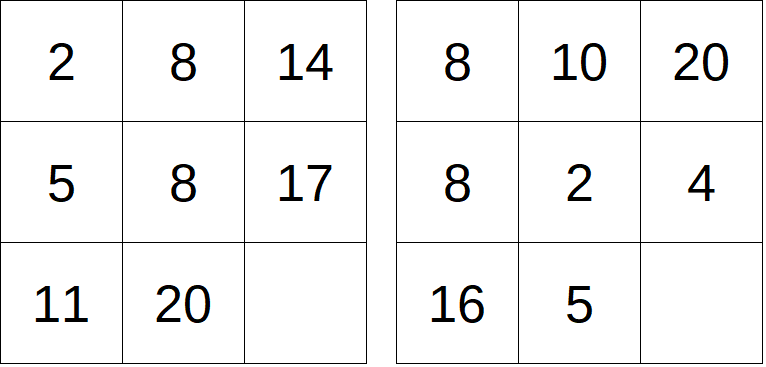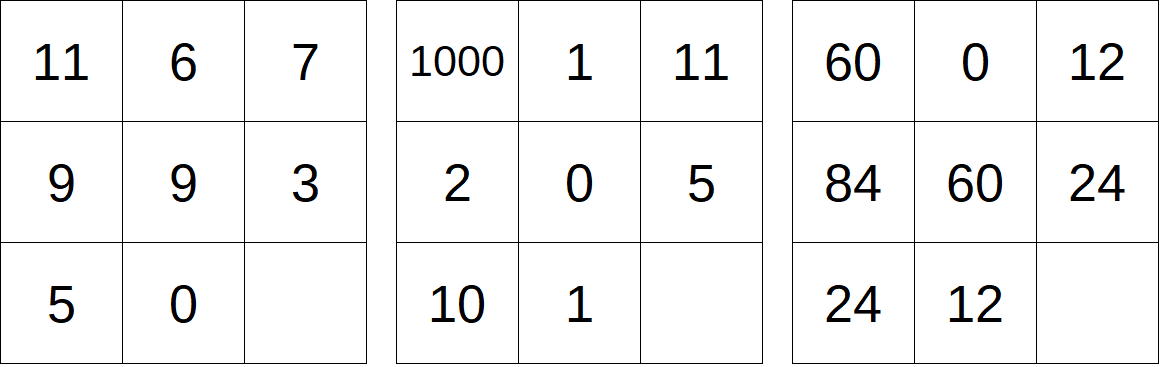Cosa vi richiama alla mente Trafalgar Square? Sicuramente la colonna con la statua dell’ammiraglio Horatio Nelson, che a Trafalgar, al largo della costa sud-occidentale della Spagna, sconfisse nel 1805 le flotte della Francia napoleonica e della Spagna. E poi i quattro leoni di bronzo che fanno da guardia alla base della statua, opera di sir Edwin Landseer, completata nel 1867 tra mille polemiche sulla regolare assegnazione dei lavori.
Se siete appassionati di matematica, invece, avrete sicuramente incontrato questo problema: da quale distanza bisogna guardare la colonna, perché l’altezza percepita della statua sia massima?
Nella scorsa estate c’è stata però una curiosità in più. Una serie di nove puzzle matematici scritti con il gesso sul pavimento della piazza da un giovane artista slovacco.
I puzzle matematici di Trafalgar Square
A raccontare la storia è il sito Transum.org, che riporta la griglia dei nove puzzle tracciati sul pavimento della piazza.
Le regole sono semplici. Si hanno quattro minuti per risolvere quanti più puzzle è possibile, deducendo la logica di successione dei numeri e riempendo di conseguenza l’ultima casella. Al termine si può scrivere il proprio nome nello spazio appena sopra i puzzle ed eventualmente lasciare un obolo.
Dal più semplice al più difficile
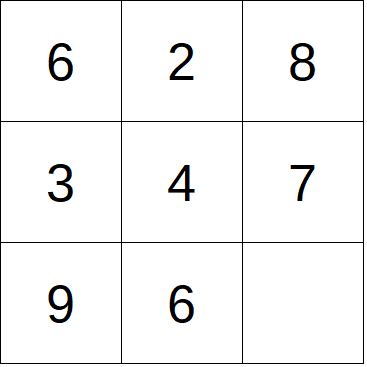La difficoltà dei puzzle è crescente, dal Livello 1 al livello 9. Il primo, riprodotto qui accanto, pone quindi una sfida molto semplice.
Non dovrebbe essere complicato, anche se, rispetto al puzzle numerico tradizionale, qui non siamo di fronte a una sequenza a cui aggiungere un ulteriore numero, dopo aver scoperto la logica nascosta che genera la sequenza.
L’analisi qui deve scoprire una logica bidimensionale, che nel caso del primo livello è molto semplice.
Cosa lega 6, 2 e 8 ? Potrebbe essere 8 = 6 + 2.
Funziona anche con la seconda riga? 7= 3+ 4, sì, funziona!
Lo stesso avviene con le prime due colonne, quindi possiamo provare a indovinare il numero mancante:
8 + 7 = 9 + 6 = 15.
Nella pagina Transum.org sono riportate griglie simili, con cui ci si può allenare. La logica della prima griglia è esattamente quella appena descritta. Provate a inserire il numero giusto nell’ultima cella e poi cliccare sul pulsante Check posto sotto le nove griglie. La spunta verde ci conferma che la nostra deduzione è corretta.
I due successivi livelli, il 2 e il 3, non comportano grandi difficoltà.
Siamo ancora nel campo delle quattro operazioni. Non si tratta dell’addizione ma di… Insomma, è semplice.
Intrigati dai puzzle matematici e dalle sequenze di numeri? Date un’occhiata alla Congettura di Collatz!
Un pizzico di difficoltà in più
I due livelli successivi, il 4 e il 5, presentano una difficoltà lievemente superiore.
Rimaniamo nel campo delle quattro operazioni, anzi, dell’addizione: 2 + 8 = 10, ma il successore è 14. Alla seconda riga, 5 + 8 = 13, ma il successore è 17.
Scatta un campanello di allarme? Da 10 a 14, da 13 a 17, sembra che la logica per costruire il successore sia:
somma i primi due numeri e aggiungi 4
Torna con le prime due colonne? Sì.
Per il livello successivo, il 5, bisogna spremere un po’ di più le meningi. Vediamo: il successore a volte cresce (8, 10, 20), a volte diminuisce (8, 2, 4). Suggerimento: che legame c’è tra il prodotto dei primi due elementi della successione (80, 16) e il terzo numero (20, 4)? Sembra che il prodotto sia 4 volte il terzo numero. Torna con le due colonne? Sì! Quindi la logica potrebbe essere:
successore = metà del primo x metà del secondo
Bene, siamo a cinque puzzle matematici risolti su nove.
Il livello 6, piccola difficoltà in più
Al livello successivo, il 6, cresce la complessità di ragionamento. Proviamo a lavorare sulla seconda riga, che ha i numeri più piccoli, e il terzo termine, il 7, dispari.
Cosa può generare 7?
1 x 7, 1 + 6, 3 + 4, …
Proviamo a sposare i primi due termini della riga, 6 e 6, con queste ipotesi.
Escludiamo il primo, 1 x 7, non c’è somiglianza.
Proviamo con il secondo, 1 + 6. La logica potrebbe essere:
un sesto del primo + il secondo
anche scambiando di ruolo primo e secondo. Ma non torna, nelle altre righe e colonne ci sono numeri non divisibili per 6.
La terza, invece, potrebbe funzionare:
metà del primo + il secondo diminuito di due
6/2 + (6-2) = 3 + 4 = 7
12/2 + (6 – 2) = 6 + 4 = 10
Per ora funziona. Proviamo anche con la prima riga e la seconda colonna. Funziona? Bene!
Alla fin fine sembra davvero tutto semplice, vero?
Proviamo gli ultimi tre livelli
Il livello dei puzzle matematici dal 7 al 9 è decisamente tosto.
Per me il più oscuro rimane il puzzle 8, alla fin fine anche il 9 è dominabile con un po’ di riflessione. Ma l’8?
Per un approfondimento: la questione dei nove puzzle matematici di Trafalgar Square ha generato una discussione su Reddit.
Nella discussione è anche riportata un’osservazione divertente oltre che interessante, applicabile a tutti i puzzle matematici di questo tipo:
Rispondete sempre 19, e non sbaglierete mai.
Perché 19? Semplice. Il metodo di interpolazione di Lagrange consente di determinare un polinomio di grado n che abbia il valore desiderato in n determinati punti. Quindi, dati un certo numero di termini, diciamo quattro, di cui si desidera il successore, basta aggiungere un successore a caso, mettiamo 19, e il metodo di interpolazione di Lagrange ci darà una solida giustificazione matematica al legame tra i quattro numeri dati e il nostro 19.
Se entro sera non trovo la soluzione al puzzle numero 8, ci piazzo un 19 e non ci penso più.
Articoli correlati:
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
