Agli inizi dell’800 una giovane matematica francese, Sophie Germain, sistemava un tassello importante nella storia della dimostrazione della Congettura di Fermat, meglio nota come Ultimo Teorema di Fermat. Ma, per poter essere presa in considerazione, Sophie era stata costretta a fingersi uomo, firmandosi Monsieur Le Blanc.
L’ultimo teorema, da Fermat a Wiles, passando per Sophie Germain
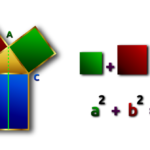
Tutti ricordano, o dovrebbero ricordare, il teorema di Pitagora, che lega le misure dei cateti e dell’ipotenusa di un triangolo rettangolo. Numericamente, se a e b sono le misure dei cateti e c quella dell’ipotenusa, si ha:
a2 + b2 = c2
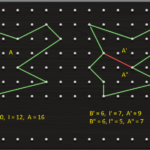
Esistono infinite terne di numeri interi a, b e c che soddisfano questa equazione.
La più semplice è la terna 3, 4 e 5, visto che 32 + 42 = 52. Nota fin dall’antichità, questa terna era utilizzata dagli Egizi per suddividere le terre appena liberata dalle piene del Nilo, tracciando angoli retti sul terreno con l’aiuto di corde. Da qui il nome di tenditori di corde con cui erano anche identificati gli antichi Egizi.
Nel 1637 il francese Pierre de Fermat, magistrato di professione e matematico per hobby, analizzando l’equazione:
an + bn = cn
mentre leggeva una copia dell’Arithmetica di Diofanto di Alessandria, si convinse di aver trovato una dimostrazione mirabile, del fatto che tale equazione non avesse soluzione per a, b e c interi, quando n è un intero maggiore di 2. Dimostrazione che, però, non riusciva a riportare nell’esiguo margine del libro:
[…] demostrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.
Il caso dei quadrati, con le sue infinite soluzioni, sarebbe quindi un’eccezione, mentre per qualunque potenza maggiore di 2 varrebbe la regola di non esistenza di soluzioni intere.
Una dimostrazione che ha atteso 350 anni
Fermat non tornò più sulla questione, e la sua congettura è stata dimostrata definitivamente solo nel 1994, dall’inglese Andrew John Wiles, utilizzando conoscenze sviluppate nella seconda parte del ‘900. Inoltre la prima stesura della dimostrazione di Wiles copre 200 pagine, poi ridotte a 130 razionalizzando e semplificando. È quindi probabile che la prova di Fermat non fosse corretta.
Nel tragitto da Fermat a Wiles ci furono pochi risultati notevoli prima di Sophie Germain: lo stesso Fermat in un altro lavoro diede la prova per n = 4; Eulero provò la Congettura per n = 3.
Sophie Germain, offrendo una prova per un’intera classe di numeri primi, ridestò l’interesse per una dimostrazione completa. Interesse che rimase vivo per tutto l’800, prima di riassopirsi in attesa di Wiles.
Chi era Sophie Germain?
Mentre infuria la protesta popolare che porterà all’assalto al carcere-fortezza della Bastiglia (14 luglio 1789), in rue Saint-Denis una ragazzina tredicenne divora i libri della biblioteca di famiglia. Si chiama Sophie Germain ed è nata a Parigi il 1° aprile del 1776.

Un libro, in particolare, racconta la morte di Archimede: i soldati romani al comando di Marcello, piegata la strenua difesa dei Siracusani, invadono la città. Secondo la leggenda, Archimede, preso nella risoluzione di un problema di geometria, non obbedì al soldato che gli ordinava di seguirlo. Al suo rifiuto, il soldato lo trafisse con la lancia.
Quanto forte doveva essere l’interesse per quel problema, per far ignorare ad Archimede la più elementare cautela per la propria sopravvivenza? Sophie è letteralmente rapita da quell’episodio e si appassiona alla matematica. Legge libri su libri, giorno e notte.
Il padre di Sophie, Ambroise-François Germain, le tenta tutte per riportare gli interessi della figlia nell’ambito normale per un’adolescente. Arriva persino a nasconderle le candele, indispensabili per la lettura notturna, e a non riscaldare la biblioteca di notte. Ma non c’è verso, Sophie si avvolge nelle coperte e nasconde una riserva segreta di candele.
Il pensiero scientifico non è cosa per donne
L’esperienza della piccola Sophie, che scopre l’amore per la matematica leggendo il racconto della morte di Archimede, non è cosa comune sul finire del ‘700.
Certo, una gentil-fanciulla non può e non deve ignorare i progressi scientifici (la conversazione con cui la intrattiene un gentiluomo potrebbe incautamente scivolare su questi argomenti). Ma d’altro canto i testi crudamente scientifici sono inadeguati (è una gentil-dama, perbacco!).
Occorrono quindi testi adatti, anzi adattati. Un esempio:
Il newtonianismo per le dame, ovvero Dialoghi sopra la luce, i colori, e l’attrazione
scritto dal conte Francesco Algarotti e pubblicato il 1 gennaio 1739, a spese di Giambattista Pasquali, libraio e stampatore di Venezia
L’autore, in villeggiatura con un’immaginaria Marchesa E…, la introduce alle meraviglie della teoria gravitazionale di Newton e dei suoi effetti, maree incluse.
Un efficace modo, per giustificare che l’attrazione gravitazionale tra due corpi varia con l’inverso del quadrato della loro distanza, è quello di immaginare il campo gravitazionale di un corpo come la luce di una candela. Come cambia l’intensità della luce, allontanandosi dalla candela?
Immaginiamo delle sfere di diametro via via maggiore, con centro nella fiamma della candela. La luce si diffonde in tutte le direzioni, quindi a una certa distanza x dovrà distribuirsi su tutta la superficie della sfera, pari a 4 π x2. L’intensità si riduce perciò con l’inverso del quadrato della distanza: raddoppiando la distanza, l’intensità si riduce a un quarto.
La Marchesa E… afferra immediatamente il concetto e lo traduce in un’esperienza a lei più consona, l’Amore: una separazione tanto più è lunga, tanto più fa scemare l’Amore. Ragionevole che l’intensità dell’Amore si riduca con il quadrato della durata della separazione. Dopo 8 giorni sarà quindi 64 volte meno intenso (parole della Marchesa E…).
Non so fino a che punto questa similitudine possa chiarire le cose a una fanciulla, ma un paio di perplessità ce l’ho. Primo, un affetto che si abbatta a meno di un sessantesimo dopo poco più di una settimana non mi pare abbia basi solidissime.
Secondo, come farà la marchesa E… a misurare l’intensità dell’Amore? Peccato non si possa approfondire.
Sophie Germain si iscrive all’École polytechnique
No, in realtà Sophie Germain non può iscriversi all’École polytechnique, riservata solo a studenti maschi.
Fondata nel 1794 con il nome di École centrale des travaux publics, nel 1795 diventa polytechnique, neologismo creato per rimarcare che la scuola si occupa delle molteplici declinazioni della tecnica. La rivoluzione francese ha scombinato anche la struttura scolastica, e c’è penuria di tecnici.
A Sophie è quindi precluso l’accesso, ma lei riesce a procurarsi le credenziali di uno studente che ha mollato e se ne è tornato a casa, Antoine Auguste Le Blanc.
Antoine Auguste rimarrà testimonial imperituro dei fuoricorso di tutto il mondo e di tutti i tempi.
Firmandosi Monsieur Le Blanc, Sophie riesce a procurarsi le lezioni del corso supervisionato dal matematico Joseph-Louis Lagrange, a cui fa pervenire le risoluzioni settimanali dei compiti assegnati agli studenti. E spesso le sue soluzioni sono brillanti e originali, le osservazioni acute.
Lagrange è un pezzo da 90 della matematica del ‘700 – inizi ‘800. Torinese di nascita e di studi ha successivamente insegnato prima all’Accademia di Berlino, poi si è trasferito a Parigi.
Inciso turistico: via Lagrange è nella zona pedonale al centro di Torino, termina verso il Palazzo Reale con il cioccolato di Gobino e due passi dopo c’è il Museo Egizio.
Lagrange conosce Le Blanc abbastanza da rimanere sorpreso del suo repentino miglioramento in matematica.
Lo convoca, per complimentarsi. Sophie è costretta a disvelarsi al matematico, che rimane naturalmente sorpreso. È l’inizio di una lunga amicizia, Lagrange non rivelerà la vera identità di Monsieur Le Blanc e la loro collaborazione continuerà nel tempo.
Sophie Germain scopre la Congettura di Fermat
Nei primi anni dell’800, mentre Napoleone costruisce il suo impero, Sophie Germain scopre la Congettura di Fermat e legge dei tentativi fin lì effettuati per dimostrarla.
Si rende conto che affrontare un caso per volta non è la strada giusta, e che serve un approccio completamente nuovo. E infatti la strada da lei imboccata la porterà a un risultato significativo (Teorema di Germain), dimostrando che, nel caso particolare in cui sia n che 2n + 1 sono primi, non c’è soluzione in cui n non divida il prodotto a * b * c.
Il teorema verrà reso pubblico solo nel 1823, dopo essere rimasto in 24 pagine manoscritte, con il titolo di:
Remarques sur l’impossibilité de satisfaire à l’equation xp + yp = zp
Nel 1804 non ha ancora raggiunto il risultato, ma ha cominciato a costruirlo. Sarà sulla strada giusta? Il modo migliore per scoprirlo è contattare la massima autorità matematica riconosciuta, il prussiano Johann Friedrich Carl Gauss. Ed è così che il 21 novembre Monsieur Le Blanc riprende carta, penna e calamaio.
Gauss non si è mai cimentato con la Congettura di Fermat, o forse ha provato ma senza risultato. L’approccio del giovane Monsieur Le Blanc gli sembra però interessante e risponde. Lo scambio continua, con beneficio per entrambi.
Anche Gauss scopre la copertura di Sophie
Intanto Napoleone continua nelle sue campagne e nel 1806 è giunto il momento di invadere la Prussia. Sophie teme per la vita di Gauss e si raccomanda quindi a un amico di famiglia impegnato in Prussia, il generale Joseph-Marie Pernety.
Quando il generale incontra Gauss, lo rassicura e l’informa di aver ricevuto raccomandazioni da Mademoiselle Germain.
E chi è, si chiede Gauss. Ancora una volta la copertura di Sophie cade, e ancora una volta c’è la sorpresa di trovare una donna dietro risultati matematici di estremo valore:
quando una persona del sesso che, secondo i nostri costumi e pregiudizi, deve incontrare difficoltà infinitamente superiori a quelle degli uomini nel familiarizzare con queste scabrose ricerche, riesce nondimeno a sormontare gli ostacoli e a penetrare le parti più oscure della materia, allora senza dubbio ella deve possedere il coraggio più elevato, talenti straordinari e un genio superiore.
Una vita troppo breve
Sophie Germain avrà altri interessi oltre alla Congettura di Fermat. In particolare sarà la sola a rispondere a un bando per la modellizzazione matematica della propagazione di vibrazioni su superfici elastiche, bando posto nel 1811 e chiuso dal suo lavoro nel 1816.
Il suo contributo le costerà l’ostilità polemica di Poisson. In compenso le procurerà l’ammirazione e l’amicizia di Joseph Fourier, padre delle serie e della trasformata che prendono il suo nome (e che terrorizzano schiere di studenti di Analisi).
Sophie Germain se ne andrà per un tumore al seno il 27 giugno del 1831, a soli 55 anni.
Foto di apertura del post da: europeanwomeninmaths.org
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.