PEMDAS è l’acronimo di: Parentesi, Esponenti, Moltiplicazioni, Divisioni, Addizioni, Sottrazioni, ed indica l’ordine con cui eseguire le operazioni nelle espressioni algebriche, se non si vuole incorrere in errori.
Molto diffusa nelle scuole di lingua inglese, questa regola mnemonica è conosciuta in diverse varianti, tutte equivalenti: BEMDAS, BIMDAS, BOMDAS. E in Italia? Non mi risulta che venga insegnata ai nostri ragazzi delle medie, ed è un peccato.
Perché serve una regola
Chi non è incappato su Facebook in un quiz algebrico del tipo:
Solo per geni! Quanto fa: 3 – 3 x 6 + 2 = ?
Nelle risposte si trovano, oltre a quello giusto, almeno altri due risultati, popolari ma ahimè errati. Perché avviene questo? Il problema sta nel fatto che non tutti seguono le regole corrette associate alla definizione delle operazioni algebriche.
C’è chi esegue i calcoli da sinistra a destra, uno per volta:
3 – 3 = 0
0 x 6 = 0
0 + 2 = 2
Questo è l’errore più comune. Chi lo commette ignora (o ha dimenticato) le regole corrette, pur eseguendo i calcoli con un certo ordine.
Altri eseguono correttamente prima la moltiplicazione (3 x 6 = 18), ma poi si impappinano con i segni e tirano fuori 17 come risultato.
Spesso si accendono vivaci dibattiti, non gravi come quelli sull’utilità dei vaccini, ma altrettanto rivelatori di una pericolosa attitudine all’interpretazione personale delle materie scientifiche:
- Bho !!! Non so che conti fate ? Sarò matto io , ma per me il risultato e : 2
- Fa 2 ma che vi bucate tutti 😂
- 17 ovvio
- -13 come il vostro qi 😜
- Impressionante vedere quanti non sanno la matematica, ci credo ci sia bisogno del reddito di cittadinanza, se è questa la forza lavoro meglio lasciar perdere , fa -13
- Aaahhhaaaahhhhaaaa più leggo le risposte più capisco perché gli alieni non ci vengono a fare visita
Qual è l’ordine giusto
La definizione delle operazioni algebriche si accompagna a delle precise regole per la corretta esecuzione del calcolo (Parentesi, Esponenti, Moltiplicazioni, Divisioni, Addizioni, Sottrazioni):
- ogni coppia di parentesi delimita un’espressione che va risolta prima di ogni altra operazione, a partire dalle coppie di parentesi più interne;
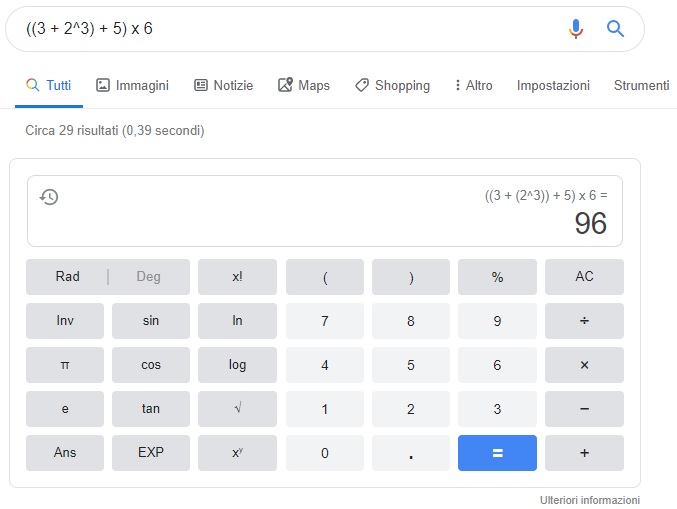
- esempio: nell’espressione ((3 + 2^3) + 5) x 6, si calcola prima (3 + 2^3), poi si risolve (… + 5), poi si conclude moltiplicando per 6;
- all’interno di ogni espressione, la prima operazione da effettuare è l’elevamento a potenza;
- seguono moltiplicazioni e divisioni, nell’ordine in cui sono disposte, da sinistra a destra;
- infine addizioni e moltiplicazioni, anche queste nell’ordine detto.
La nostra espressione va risolta quindi così:
((3 + 2^3) + 5) x 6 =
= ((3 + 8) + 5) x 6 =
= (11 + 5) x 6 =
= 16 x 6 = 96
Sarà giusto? Google ci dà una mano a verificare:
Una verifica è possibile anche con Excel o l’equivalente LibreOffice Calc, basta premettere il segno di uguale all’espressione, e utilizzare i simboli adatti per moltiplicazioni e divisioni:
=((3 + 2^3) + 5) * 6
Inserendo questa espressione in una cella, ne verrà visualizzato il valore, 96. Quindi anche Excel & Co, come la calcolatrice di Google, si direbbe che segua la regola PEMDAS.
Oltre a integrare una calcolatrice scientifica di utilizzo molto semplice, il motore di ricerca di Google consente anche di disegnare grafici sia 2D che 3D. Qualche suggerimento al riguardo si trova su questo articolo di InchiostroVirtuale.
Excel e la regola PEMDAS
In realtà non è esattamente così, per Excel (e LibreOffice Calc). Si consideri la seguente espressione:
– 3^2
Secondo la regola PEMDAS, prima eleviamo 3 al quadrato, ottenendo 9, poi consideriamo il segno meno posto davanti. Quindi il risultato è -9.
Excel fa invece un po’ di confusione. Provate a inserire in tre celle di un foglio Excel queste espressioni:
= – 3^2
= 0 – 3^2
= -3^2 + 0
Il risultato dovrebbe essere uguale a – 9, in tutti e tre i casi, giusto? Per convincersene si può chiedere alla calcolatrice di Google, basta digitare una per volta le tre espressioni nella barra di ricerca.
Invece con Excel solo la seconda espressione darà questo risultato, mentre la prima e la terza daranno 9.
Cosa è accaduto? Il segno meno in inizio di espressione non viene considerato da Excel meno prioritario dell’elevamento a potenza, come dovrebbe essere, ma più prioritario, come se avessimo scritto (-3)^2.
Un errore di Excel? Si direbbe proprio di sì, ma, seppure in casa Microsoft si siano posti il problema, avranno concluso che è impossibile da correggere, se si vuole mantenere l’assoluta compatibilità con i fogli di calcolo costruiti in giro per il mondo.
Come evitare possibili fraintendimenti? Si può utilizzare la prima regola (le parentesi) per forzare l’ordine di esecuzione. Così:
= – (3^2)
darà il risultato giusto anche con Excel. Nel caso di dubbi di interpretazione, quindi, meglio abbondare con le parentesi.
PEMDAS, BEMDAS, BOMDAS e BIMDAS
L’acronimo PEMDAS è quello diffuso nelle scuole statunitensi, dove le parentesi tonde diventano parenthesis e gli esponenti exponents.
Nel Regno Unito, invece, è diffuso BOMDAS, visto che le parentesi diventano brackets e gli esponenti orders. Lo stesso vale in Australia, e in diverse nazioni africane, come la Nigeria. In UK è anche diffusa la variante BIMDAS, in cui gli esponenti sono indicati come index.
Per ficcare bene la regola nella mente dei ragazzi, negli US si utilizza anche la frase: “Please Excuse My Dear Aunt Sally”. Non costerebbe molto immaginare una frase in italiano che richiami l’acronimo.
Esempio: “Per Evitare Molti Danni Alla Salute”. Ma sono sicuro ci sia di meglio.
Perché siamo così riluttanti ad accettare che la scienza non è democratica?
Colpa della scuola, non v’è dubbio, o meglio colpa di come sia degenerato nel tempo l’insegnamento e di un malinteso significato attribuito all’obbligatorietà della frequenza scolastica.
Obbligo scolastico fino a 16 anni non vuol dire promozione garantita fino a quell’età. Semplicemente bisognerebbe insistere, fino a quell’età, affinché anche una capra (o chi non abbia voglia di studiare) apprenda correttamente. Adeguare le aspettative alle capacità dell’allievo, invece, è terribilmente sbagliato, tutto diventa opinabile.
Ci ritroviamo così chi non sa eseguire semplici calcoli, e pretende di essere nel giusto. O anche che misura a peso una supposta pericolosità dei vaccini, per pura ricerca di consenso.
Riusciremo a fermare questa discesa agli inferi?
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.