Cosa sono i numeri socievoli e da dove spuntano?
La storia comincia da lontano, dalla scuola di Pitagora, grosso modo nel 500 a.C. Qualcuno nota che il numero 6 ha una curiosa caratteristica: se si sommano i suoi divisori propri (1, 2, 3), si ottiene proprio 6.
Una caratteristica così particolare, notano i Pitagorici, ce l’ha anche il numero 28, i cui divisori propri sono 1, 2, 4, 7, 14. Se si sommano, il risultato fa 28. Questa caratteristica dà un senso di perfezione a 6 e 28, che perciò vengono denominati numeri perfetti.
Grazie a prova e riprova, i Pitagorici riescono a trovare anche i due perfetti successivi: 496 e 8128. Sarà però Euclide, quasi un paio di secoli dopo, a trovare una condizione forte che deve possedere un numero (pari) per essere perfetto: deve essere della forma
2n-1 × (2n – 1), con (2n – 1) primo
Questa scoperta da un lato semplifica la ricerca dei numeri perfetti, dall’altro ne anticipa l’estrema rarità. Ad oggi sono noti appena 51 numeri perfetti, tutti pari, con un numero di cifre progressivamente più elevato. Il prossimo numero perfetto che sarà trovato avrà più dei quasi 50 milioni di cifre del massimo attualmente noto.
Oltre i numeri perfetti
Se si rilassa la condizione di perfezione, si trova un’altra interessante categoria di numeri.
Chiamiamo S(n) la somma dei divisori propri di n. La condizione di perfezione equivale a scrivere: n = S(n). Immaginiamo ora che si verifichi una condizione di questo tipo:
S(a) = b e S(b) = a.
Il legame tra i numeri a e b è particolare, al punto che i Pitagorici, ancora loro, li definirono numeri amici. Nel nono secolo il matematico arabo Thebit, proveniente dall’attuale Siria, trovò delle condizioni di esistenza simili a quelle trovate da Euclide per i numeri perfetti. Queste condizioni saranno poi perfezionate a metà del ‘700 da Eulero.
I numeri amici (oggi più comunemente chiamati numeri amicabili) sono molto meno rari dei numeri perfetti. Ad oggi ne sono note 1.227.366.104 coppie. Le due coppie più piccole sono 220 e 284, 1184 e 1210.
Immaginiamo ora che si verifichi una condizione di questo tipo:
S(a) = b, S(b) = c, S(c) = d, S(d) = a.
Il legame tra i numeri a, b, c e d è ancora una volta particolare, costituisce infatti una catena chiusa che mette in relazione quattro numeri. La catena avrebbe potuto essere anche più lunga, ad oggi la catena di massima lunghezza nota lega 28 elementi. Un gruppo di numeri con questa caratteristica si dice composto da numeri socievoli.
I numeri socievoli noti sono più rari e in grandissima parte si tratta di catene di 4 elementi. Non è invece nota nessuna catena di tre elementi.
I numeri perfetti e i numeri amicabili possono essere visti come casi particolari di catene di numeri socievoli, di lunghezza rispettivamente 1 e 2. Nel seguito indicherò con socievoli tutti e tre i tipi di numero.
I numeri socievoli più da vicino
Qualche riga di codice Python può aiutare a giocare con i numeri socievoli, provando a riscoprire qualche loro caratteristica interessante. Il codice, che riporto al fondo dell’articolo, non ha ovviamente lo scopo di trovare nuove catene di numeri socievoli, ma di partire da un numero fissato e mostrare l’evoluzione della sequenza: finirà con un numero perfetto, socievole o troverà una coppia di amicabili?
Qualche esempio
Partiamo dal numero 12496. L’output del codice è come segue:
n s(n) n.divisori
12496, 14288, 19
14288, 15472, 19
15472, 14536, 9
14536, 14264, 15
14264, 12496, 7
chiusa la catena con 5 elementi!
Sono partito da un numero noto, quindi fin qui non è che il risultato dia grandi soddisfazioni, a parte constatare che il codice funziona.
Ci si potrebbe chiedere, però, come trovare numeri da cui si finisca in una catena di numeri socievoli (o amicabili o perfetti).
Pari o dispari
Prima di proseguire, è da notare che, se ad oggi non è stato trovato alcun numero perfetto dispari (e nemmeno si è dimostrato che non ce ne siano), sono invece note coppie di numeri amici dispari e catene di socievoli dispari. Ecco un esempio:
n s(n) n.divisori
21548919483, 23625285957, 287
23625285957, 24825443643, 287
24825443643, 26762383557, 143
26762383557, 25958284443, 119
25958284443, 23816997477, 143
23816997477, 21548919483, 71
chiusa la catena con 6 elementi!
Ancora una volta la fonte del numero di partenza è Wikipedia.
Una semplice regola
Supponiamo che il numero di partenza sia uguale al quadrato di un numero primo: p2. I suoi divisori propri saranno allora 1 e p, la cui somma è p + 1.
Procedendo a ritroso, possiamo dire che, se abbiamo un elemento della catena che è uguale a 1 più un primo p, allora p2 porta nella catena. Vediamo un esempio:
n s(n) n.divisori
80089, 284, 2
284, 220, 5
220, 284, 11
trovata una coppia di numeri amici!
Qui sono partito dal fatto che 283 è un numero primo e che quindi 2832 = 80089 avrà come successore 284, portandomi alla coppia di amicabili (220, 284).
Una regola più prolifica
Chiediamoci ora quale tipo di successore sia legato a un numero che sia prodotto di due primi p e q, maggiori di 2, e quindi dispari. I divisori propri di questo numero saranno 1, p e q, quindi il successore è 1 + p + q, che è un numero dispari.
Ne segue che, se il numero di partenza è un dispari che diminuito di 1 è uguale alla somma di due primi p e q, allora p × q è un predecessore del numero dato.
Ma, Goldbach permettendo, un numero pari è sempre uguale alla somma di due primi, almeno in un modo. E 80088 = 80089 – 1 non fa eccezione, essendo scomponibile come somma di due primi in 1056 modi diversi (altro codice, sempre al fondo dell’articolo). La coppia di primi che porta al più piccolo prodotto è (11, 80077), quindi 11 × 80077 = 880847 ci porterà ancora alla catena (220, 284):
n s(n) n.divisori
880847, 80089, 3
80089, 284, 2
284, 220, 5
220, 284, 11
trovata una coppia di numeri amici!
Ma anche qualunque altra delle 1056 coppie, ad esempio (1049, 79039), porterà alla stessa catena. Partendo da 82911911 = 1049 × 79039:
n s(n) n.divisori
82911911, 80089, 3
80089, 284, 2
284, 220, 5
220, 284, 11
trovata una coppia di numeri amici!
Si è trovata, quindi, un’intera categoria di numeri che portano in pochi passaggi alla catena (220, 284).
Una rete che porta alla perfezione
Ho trovato divertente applicare le due regole riportate più su, per generare un pezzetto di rete di connessioni che portano al numero perfetto 6.
Il percorso logico:
- 6 = 5 + 1, con 5 primo; quindi 52 = 25 è un predecessore di 6;
- 25 = 24 + 1, e 24 può essere espresso come somma di due primi in tre modi diversi, cioè (5,19), (7,17), (11,13);
- il prodotto di ciascuna di queste coppie (95, 119, 143) darà un predecessore dispari di 25;
- da ciascuno di questi tre numeri dispari si può risalire a un ulteriore livello di predecessori, e così via.
Il grafico qui sotto riporta (in modo parziale) la rete appena descritta:
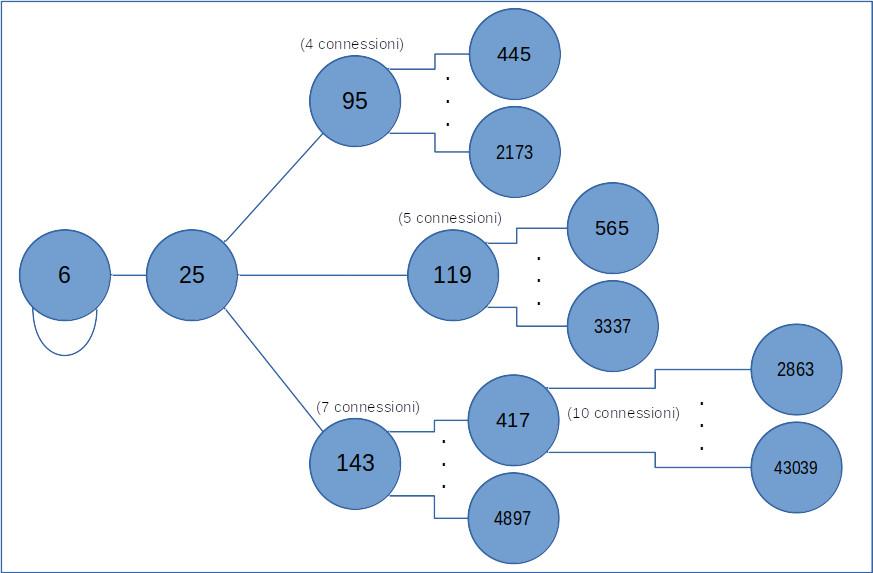Si può ovviamente continuare. Da 2863, ad esempio, si può risalire a 78 coppie di primi che sommano 2862.
Dalla coppia (5,2857), ad esempio, si può avere la seguente linea di successione in partenza da 5 × 2857 = 14285:
n s(n) n.divisori
14285, 2863, 3
2863, 417, 3
417, 143, 3
143, 25, 3
25, 6, 2
6, 6, 3
trovato un numero perfetto!
Il codice
Qui di seguito riporto i due programmi Python utilizzati il primo per costruire la catena di successori da un numero dato, l’altro per trovare le coppie di primi che sommano un numero pari dato. Entrambi i programmi sono stati sviluppati e testati su Google Colaboratory.
Costruzione della catena di successori
n = 5*2857
n_step = 300
radici = [n]
step = 0
trovato = False
#
print ('{:16}{:16}{:16}'.format(' n',' s(n)',' n.divisori'))
while step < n_step:
max = int(n**0.5)
divisori = [1]
for i in range (2 + n%2, max + 1, n%2 + 1):
if n % i == 0:
divisori.append(i)
divisori.append(int(n/i))
if len(divisori) > 1:
if divisori[-1] == divisori[-2]:
del divisori[-1]
print ('{:16},{:16},{:16}'.format(n,sum(divisori),len(divisori)))
n = sum(divisori)
if n == 1:
print ('\ntermina a 1 dopo {} passi!'.format(len(radici)))
trovato = True
break
if n == radici[-1]:
print ('\ntrovato un numero perfetto!')
trovato = True
break
if n in radici:
if radici.index(n) == len(radici)-2:
print ('\ntrovata una coppia di numeri amici!')
trovato = True
break
else:
print ('\nchiusa la catena con {} elementi!'.\
format(len(radici)-radici.index(n)))
trovato = True
break
radici.append(n)
step += 1
if not trovato:
print ('\nnessuna conclusione dopo {} passi'.format(n_step))
Coppie di primi che sommano un numero pari dato
from sympy import isprime
# n = 80088
n = 2862
conta = 0
max_conta = 100
if isprime(n - 3):
print ('{},{}'.format(3,n-3))
conta += 1
p = 5
while p < n/2:
if isprime(p) and isprime(n-p):
if conta < max_conta:
print ('{},{}'.format(p,n-p))
conta += 1
if isprime(p+2) and isprime(n-p-2):
if conta < max_conta:
print ('{},{}'.format(p+2,n-p-2))
conta += 1
p += 6
print ('\ntrovate {} coppie di primi che sommano {}'.format(conta, n))
L’immagine di apertura dell’articolo è stata ottenuta con Monkeylearn.com.
Su quel sito si può generare una word cloud, sulla base di un testo. Ho utilizzato questo testo:
Esistono numeri socievoli, amicabili e numeri perfetti.
I numeri socievoli? Una catena. Gli amicabili: solo due. i numeri perfetti: ognuno fa per sé.
I numeri socievoli sono legati dai divisori propri, inclusa l’unità: ciascun numero è uguale alla somma dei divisori propri del precedente e l’ultimo a quella dei divisori propri del primo.
Se la catena di numeri socievoli è composta da due elementi soltanto, allora questi sono chiamati numeri amicabili.
Con i numeri perfetti, infine, ogni numero è uguale ai propri divisori.
La catena di numeri socievoli più lunga nota è di 28 elementi, la lunghezza più comune è 4, non è nota nessuna catena di lunghezza 3.
Il numero di numeri amicabili noti è molto maggiore di quello dei numeri amicabili. I numeri perfetti, invece, sono molto più rari.
Il sito offre una discreta flessibilità nel configurare la nuvola ottenuta.
Articoli correlati:
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
