I numeri perfetti dispari sono oggetto di ricerca (finora infruttuosa) fin dai tempi degli antichi Greci. Una volta scoperto che alcuni numeri, come ad esempio 6, 28 e 496 avevano la proprietà di essere uguali alla metà della somma dei propri divisori, compreso il numero stesso e l’unità, era nata istintivamente la domanda: ma esistono anche numeri dispari con questa proprietà?
Dopo secoli di infruttuose ricerche, Pace Nielsen, professore della Brigham Young University di Provo, Utah, sembra aver intrapreso una strada promettente per rispondere a quella domanda.
Cos’è un numero perfetto
Il più piccolo dei numeri perfetti è 6, perché la somma dei suoi divisori, inclusa l’unità, è uguale al suo doppio:
1 + 2 + 3 + 6 = 12 = 2 * 6
Il successivo numero perfetto è 28 (divisori: 2, 4, 7, 14, 28):
1 + 2 + 4 + 7 + 14 + 28 = 56 = 2* 28
Questa proprietà dei numeri interi positivi era nota già agli antichi Greci, che trovarono anche la formula generatrice che fornisce tutti i numeri perfetti pari:
se p è primo e 2p – 1 è primo, allora 2p-1 (2p – 1) è un numero perfetto [1].
La formula dà i primi due numeri perfetti assegnando a p il valore di 2 e di 3. Infatti:
2 è primo, 22 -1 = 3 è primo, e 22-1 ( 22 -1) = 2 * 3 = 6
3 è primo, 23 -1 = 7 è primo, e 23-1 ( 23 -1) = 4 * 7 = 28
La ricerca dei numeri perfetti pari
Si deve a Eulero (1707 – 1783) la dimostrazione che la formula [1] fornisce tutti i numeri perfetti pari, che quindi sono legati a doppio filo ai primi della forma 2p – 1, anche detti numeri di Mersenne (per un approfondimento vedi l’articolo sui Repunit).
Si conoscono svariate proprietà dei numeri di Mersenne, ma non se siano o meno infiniti. Sta di fatto che sono da sempre molto studiati e non stupisce che il primato del maggior numero primo conosciuto è quasi sempre detenuto da un numero di Mersenne. Al momento il titolo spetta a 282.589.933 − 1, numero di 24.862.048 di cifre.
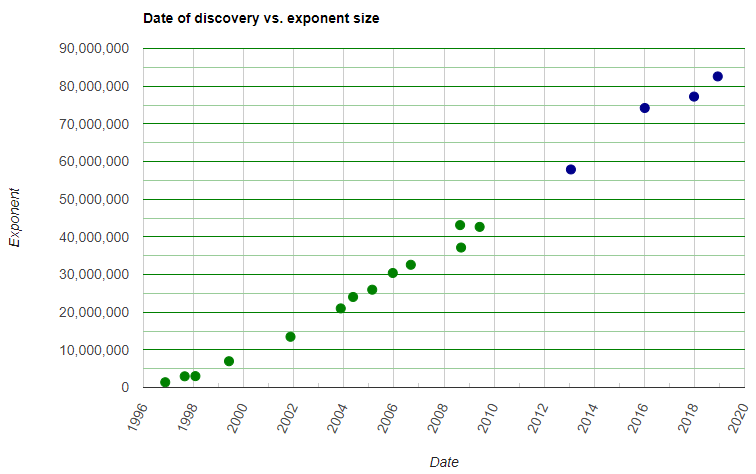
Dal 1996 è attivo il Great Internet Mersenne Prime Search (GIMPS), progetto di ricerca dei numeri di Mersenne, basato sulla capacità di calcolo di pc offerti in rete da volontari. In questi anni il GIMPS ha trovato 17 numeri di Mersenne. Nella tabella riepilogativa sul sito si trovano anche i numeri perfetti pari associati a ciascun primo di Mersenne.
Questo è l’andamento nel tempo della ricerca:
Se si aderisce al progetto si ha una probabilità, per quanto piccola, di passare alla storia!
Numeri perfetti dispari
Diverso è il discorso per i numeri perfetti dispari: per quanto si sia cercato, non ne è stato trovato nemmeno uno.
Sono state invece determinate diverse condizioni che un eventuale numero perfetto dispari dovrebbe soddisfare, e che sono talmente stringenti da portare a ipotizzare che non esista nessun numero perfetto dispari.
Già Eulero aveva dimostrato che, se esiste, un numero perfetto dispari deve essere della forma:
N = p4m+1 * Q2
dove p è un numero primo che non divide il numero intero Q.
Studi successivi hanno portato ad altre condizioni. Ad esempio, che se il numero perfetto dispari N è diviso da 3, 5 o 7, allora deve avere almeno 27 fattori primi. O, ancora, che il suo maggior fattore primo deve essere maggiore di 10.000.000.
Ricerche con algoritmi via via più raffinati hanno portato a concludere che, se esistono numeri perfetti dispari, allora devono essere maggiori di 102.000. Insomma, se dovessi scommettere, punterei sulla non esistenza dei numeri perfetti dispari.
Il punto è che, finora, tra le condizioni trovate non sono state trovate incompatibilità, nel senso di condizioni che non possano essere soddisfatte contemporaneamente da uno stesso numero, il che porterebbe a dimostrare la non esistenza di numeri perfetti dispari.
I motivi di una ricerca
Naturalmente ipotizzare è una cosa, provare è un’altra, e quindi la ricerca sull’esistenza dei numeri perfetti dispari è ancora aperta.
È lecito chiedersi del perché si spendano energie in questo tipo di ricerca. In fondo il risultato in sé (trovare un numero perfetto dispari o dimostrare che non esistono) non porterebbe a nessun vantaggio concreto per la scienza.
Quello che conta è invece il percorso logico di dimostrazione che viene sviluppato. Anche in assenza di un punto fermo, questo tipo di ricerche stimolano l’ideazione di nuovi ragionamenti sull’essenza dei numeri, che portano comunque vantaggio alla conoscenza.
Non dimentichiamo, per fare giusto un esempio, che la crittografia su cui si basa la sicurezza bancaria è strettamente legata agli algoritmi di scomposizione in fattori primi. C’è da tremare all’idea che l’eventuale scoperta di un algoritmo di fattorizzazione radicalmente più efficiente e veloce degli attuali cada nelle mani sbagliate.
La svolta di Pace Nielsen
Oggi professore della Brigham Young University di Provo, Utah, Pace Nielsen si innamorò del problema dell’esistenza dei numeri perfetti dispari quando era alle superiori, a metà degli anni ’90.
Per diversi anni il suo maggior contributo è stato quello di aggiungere nuove condizioni di esistenza, o di rendere ancora più stringenti alcune di quelle esistenti.
Di recente ha concepito un nuovo e promettente attacco al problema.
È partito da un risultato di Cartesio (1596 – 1650) che, analizzando il numero dispari:
198.585.576.189 = 32 × 72 × 112 × 132 × 22.021
ne aveva calcolato la somma dei divisori, dati i suoi fattori primi 3, 7, 11, 13 e 22.021, risultata uguale al doppio del numero stesso.
Bingo! In effetti no, c’è un piccolo particolare da considerare: 22.021 non è un numero primo, la fattorizzazione corretta del numero è:
198.585.576.189 = 32 × 72 × 112 ×132 × 192 × 61
Se si sommano i divisori in base a questa (corretta) fattorizzazione, il numero è lungi dall’essere perfetto, ma ha pur sempre una caratteristica importante: è un falso numero perfetto dispari, soddisfa la condizione di perfezione, a patto di barare sulla fattorizzazione.
Una nuova via da esplorare
L’idea di Pace Nielsen si basa sul fatto che in realtà i veri numero perfetti dispari (ammesso che esistano) sono un sottoinsieme dei falsi numeri perfetti dispari. Le condizioni di esistenza di questi ultimi sono ancora tutte da scoprire, e c’è la speranza di trovare per questa strada quella impossibilità di esistenza a cui finora non si è ancora arrivati per la via diretta.
Per il momento è stata allargata la base di regole da infrangere. Oltre al fattore non primo dell’esempio di 198.585.576.189, il team di lavoro di Pace Nielsen considera anche fattorizzazioni con fattori primi negativi e fattori ripetuti. Quindi ammettere come fattori nella scomposizione anche numeri come -127, oppure considerare 72 × 72 al posto di 74:
−22.017.975.903 = 34 × 72 × 112 × 192 × (−127)1
-101.411.037 = 32 × 72 × 72 × 131 × (−19)2
È difficile prevedere se la strada intrapresa da Pace Nielsen sarà o meno quella giusta. In ogni caso, anche se non dovesse portare a dimostrare la non esistenza dei numeri perfetti dispari, quasi certamente aggiungerà qualcosa nella nostra conoscenza sulla natura dei numeri.
Foto di apertura di Alicja da Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.