Si può fare aritmetica con il domino? Sì, e ce lo dimostra il blog mathequalslove.net.
Credo che tutti abbiano giocato con il domino in qualche momento della vita. Per me è stato quando la mia Valentina era alle elementari.
Finita la colazione, mia moglie schizzava a scuola ben prima delle 8 mentre noi due, in attesa di andare a scuola, giocavamo una decina di minuti. Costruivamo delle sequenze, depositando alternativamente una tessera. Non ricordo però esattamente quali regole seguissimo per giocare con le 28 tessere del gioco:
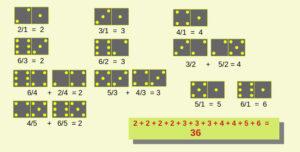
Come si fa aritmetica con il domino? Ad ogni tessera si può far corrispondere una frazione, in cui numeratore e denominatore sono uguali al numero di pallini presenti nelle due metà della tessera. Esempio: alla tessera con 4 e 6 pallini si possono far corrispondere le frazioni 4/6 oppure 6/4.
È evidente che la tessera in alto a sinistra (0/0) va esclusa dal gioco.
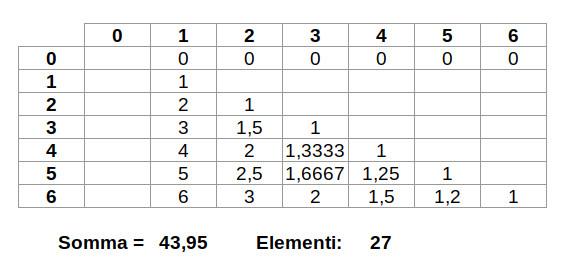
Bene, il post del blog chiede di distribuire le restanti 27 tessere del domino nello schema che segue:
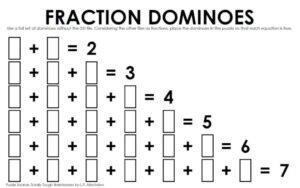
in modo che tornino le somme indicate.
Il gioco è stato in realtà originariamente pubblicato su Puzzles of Leonid Mochalov, che fornisce anche una soluzione.
L’analisi del gioco: prime considerazioni
La prima tentazione è stata quella di mettere giù un programmino Python che scorresse le possibili disposizioni delle 27 tessere, considerando entrambe le possibili frazioni collegate, fino a trovare quelle che rispondessero correttamente al problema.
Momento di realismo immediato: era evidentissimo che non ne sarei mai venuto a capo, meglio cominciare a giocare manualmente, per trovare eventuali possibili semplificazioni dell’algoritmo.
Prima considerazione: le 27 tessere devono essere orientate in modo che la somma delle relative frazioni dia:
2 + 3 + 4 + 5 + 6 + 7 = 27
Appena sistemate le tessere sul tavolo ci si accorge di alcune semplificazioni iniziali:
- le sei tessere 0-1, 0-2, 0-3, 0-4, 0-5, 0-6 possono essere associate solo con le frazioni con 0 a numeratore, e danno contributo nullo alle somme; serviranno quindi come riempitivi per far tornare il numero di tessere in ogni riga;
- le sei tessere 1-1, 2-2, 3-3, 4-4, 5-5, 6-6 possono essere associate ciascuna a una sola frazione di valore 1.
È possibile allora lavorare sulle restanti 15 tessere, da orientare in modo che la somma dia 27 – 6 = 21.
Provando e riprovando
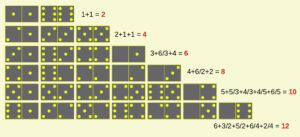
Disposte le 15 tessere sul tavolo, ho provato a raggrupparle in modo che, da singole o a coppie, avessero come valore un numero intero. Sposta qui, metti là, gira un paio di tessere per aumentare o diminuire la somma totale, alla fine ho ottenuto questi raggruppamenti:
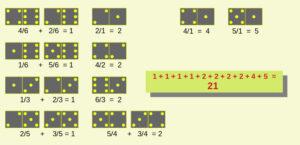Abbiamo quindi raggruppato le tessere in modo che, insieme alle 12 messe da parte, dovrebbe essere possibile completare correttamente la tabella delle somme.
Ultimo passaggio: riempiamo la tabella
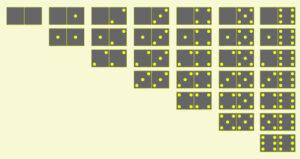
A questo punto, sempre procedendo manualmente, ho distribuito nella tabella i gruppi di tessere appena trovati, in modo da raggiungere esattamente le somme richieste. Questa è la disposizione a cui sono arrivato:
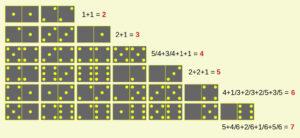
E questa disposizione delle tessere soddisfa il problema posto da mathequalslove.net.
Quante soluzioni esistono?
Nel mio processo manuale ho lasciate inesplorate diverse strade alternative. In particolare:
- non ho analizzato i casi in cui concorrevano non due, ma tre o più tessere a comporre un intero (e la soluzione proposta sul sito di Leonid Mochalov ha proprio questa caratteristica);
- esistono presumibilmente alternative alla mia selezione di accoppiamenti, per giungere al totale di 27;
- nella disposizione finale è possibile scambiare elementi con lo stesso valore tra righe diverse, ottenendo quindi soluzioni differenti.
Quindi è chiaro che di soluzioni ne esistono in quantità, cosa che spiega anche la facilità con cui sono riuscito a trovarne una. A questo punto però la voglia di mettere su un algoritmo per trovare tutte le soluzioni possibili è decisamente scemata.
Una divertente variante
Visto che però la voglia di giocare non era stata soddisfatta appieno, ho pensato a una variante dell’aritmetica del domino: quale sarà la massima somma intera che posso raggiungere con le tessere del domino?
La risposta si ottiene con una relativa semplicità: posiziono tutte le tessere in modo da ottenere frazioni di valore uguale o maggiore di 1, poi, se la somma non è un numero intero, faccio un minimo di aggiustamenti per ottenere un numero intero.
Al primo passaggio (trovare il massimo valore possibile) ottengo:
Nonostante vari tentativi non ho trovato una disposizione delle tessere che mi dia 43, ma ne ho trovato una che arriva a 42. Nell’immagine che segue si vede il relativo raggruppamento delle 15 tessere su cui giostrare. La somma dei valori è 36, a cui vanno aggiunti i 6 punti delle tessere 1-1, 2-2, 3-3, …
Ora, 42 è un numero particolarissimo, almeno se si è letta la Guida intergalattica per autostoppisti, ed è stato anche protagonista di un articolo qui, su Inchiostro Virtuale.
Ma 42 è interessante anche nell’aritmetica del domino. Infatti si può scrivere 42 = 2 + 4 + 6 + 8 + 10 + 12, quindi dovrebbe essere possibile disporre le tessere in uno schema simile a quello proposto da MathEqualsLove, ma con somme di riga in progressione aritmetica di ragione 2.
Ed è possibile!
Se mi fossi avventurato sulla strada del programma in Python è probabile che sarei ancora impantanato a realizzare l’algoritmo. A volte la strada manuale è più agevole, magari non dà risposte esaustive, ma ci si diverte almeno in ugual misura.
L’immagine di apertura è di Peggy und Marco Lachmann-Anke e proviene dal sito Pixabay.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
Articoli correlati:
