Ho studiato statistica (le basi, senza esagerare) e l’ho utilizzata per lavoro, quindi la maneggio con una relativa sicurezza. E quando ho un dubbio, spesso ricorrere alla statistica dei dadi mi aiuta a chiarirmelo.
Stavolta, però, grazie proprio a un articolo sulla statistica dei dadi, mi sono ritrovato in quello che a prima vista sembra un paradosso.
L’articolo WriteUp — Daily Coding Problem (10) di Nicola Moro su Medium.com propone due giochi consistenti nel lancio ripetuto di un dado, fino a che:
- si ottiene una sequenza di due 5;
- si ottiene un 5 seguito da un 6.
Con quale dei due si vince, in media, con una sequenza di lanci più corta?
Risposta istintiva: non cambia nulla tra i due giochi, perché ogni lancio del dado è statisticamente indipendente dai precedenti. Quindi la probabilità che, una volta uscito un 5, al successivo lancio esca ancora un 5 è 1⁄6, esattamente come è 1⁄6 la probabilità che al 5 segua un 6.
Sbagliato, vediamo perché.
Una rappresentazione grafica dei due casi
È possibile rappresentare ciascuno dei due giochi mediante un grafo, composto da degli stati e dalle transizioni tra gli stati.
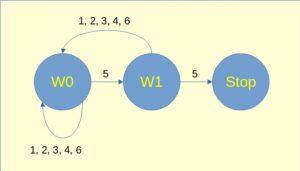
Ecco il grafo del primo gioco, quello che termina con la sequenza 55:
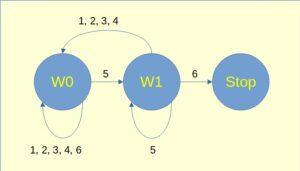
E il grafo del secondo gioco, che termina quando si ottiene la sequenza 56:
Gli stati W0 e W1 sono stati di attesa, e gli archi orientati descrivono il passaggio da uno stato al successivo, a seconda del valore estratto con il dado.
Il tempo medio di gioco, secondo la statistica dei dadi
Il gioco “55”
Chiamiamo w0 e w1 il numero di lanci che occorre attendere, in media, per arrivare allo stato Stop, rispettivamente nei due stati W0 e W1 . Prima del primo lancio siamo nello stato W0.
Nel caso del primo gioco, il “55”, si ha:
- se siamo nello stato W0, occorrerà necessariamente lanciare ancora una volta e poi, in 5 casi su 6 si rimarrà nello stato W0 e in un caso si passerà allo stato W1; quindi:
w0 = 1 + 5⁄6 w0 + 1⁄6 w1; - se siamo nello stato W1, occorrerà necessariamente lanciare ancora una volta e poi, in 5 casi su 6, si ritornerà nello stato W0 e in un caso si passerà allo stato finale Stop, dove non sarà più necessario lanciare ancora il dado; quindi:
w1 = 1 + 5⁄6 w0 + 1⁄6 × 0.
A questo punto basterà risolvere il sistema di due equazioni nelle due incognite w0 e w1.
Dalla seconda equazione si ha: w1 = 1 + 5⁄6 w0 e, sostituendo nella prima, si ha:
w0 = 1 + 5⁄6 w0 + 1⁄6 (1 + 5⁄6 w0), che semplificata dà:
36 w0 = 36 + 30 w0 + 6 + 5 w0 . Raccogliendo i termini, infine, si trova:
w0 = 42.
Quindi, nel caso del gioco “55”, occorrerà attendere in media 42 lanci, prima di ottenere la sequenza di due 5 consecutivi.
Il gioco “56”
Nel caso del secondo gioco, il “56”, si ha:
- se siamo nello stato W0, occorrerà necessariamente lanciare ancora una volta e poi, in 5 casi su 6, si rimarrà nello stato W0 e in un caso si passerà allo stato W1; quindi:
w0 = 1 + 5⁄6 w0 + 1⁄6 w1; - se siamo nello stato W1, occorrerà necessariamente lanciare ancora una volta e poi, in 4 casi su 6, si ritornerà nello stato W0, in un caso si rimarrà nello stato W1 e in un caso si passerà allo stato finale Stop, dove non sarà più necessario lanciare ancora il dado; quindi:
w1 = 1 + 4⁄6 w0 + 1⁄6 × w1 + 1⁄6 × 0.
Dalla prima equazione si ha: 6 w0 = 6 + 5 w0 + w1, che semplificata dà: w0 = 6 + w1.
Sostituendo nella seconda equazione, si ha:
w1 = 1 + 4⁄6 (6 + w1) + 1⁄6 × w1, che semplificata dà:
6 w1 = 6 + 24 + 4 w1 + w1 . Raccogliendo i termini, infine, si trova: w1 = 30.
Infine: w0 = 6 + w1 = 6 + 30 = 36.
Quindi, nel caso del gioco “56”, occorrerà attendere in media 36 lanci, prima di ottenere la sequenza di due 5 consecutivi.
Ma perché il gioco “56” finisce prima?
Contrariamente a quanto avevo concluso inizialmente, quindi, i due giochi non sono statisticamente equivalenti, ma ottenere la sequenza “56” è più probabile che ottenere la sequenza “55”.
Il motivo si può ricavare osservando con attenzione i due grafi riportati in precedenza.
Nel caso del gioco “56”, quando si è nello stato W1 ci sono due esiti del lancio del dado che sono uno favorevole e l’altro non del tutto sfavorevole: se esce 6, il gioco si conclude, se esce 5, invece, si rimane nello stato W1, con la possibilità di chiudere al lancio successivo.
Nel caso del gioco “55”, invece, manca il caso non del tutto sfavorevole; se non esce il secondo 5, occorre ritornare a W0, da cui serviranno almeno due ulteriori lanci per terminare.
Testiamo la statistica dei dadi con Excel
È il momento di verificare con una simulazione se davvero le cose stanno così.
Nell’articolo su Medium l’autore riporta una simulazione in linguaggio GO, che esegue i due giochi per un elevato numero di volte.
Nella mia sconfinata pigrizia, ho preferito ricorrere ad Excel, anzi, a LibreOffice Calc, effettuando una simulazione di portata molto più modesta, ricavando però dei grafici facili facili. Lo so, con poche righe di Python avrei potuto realizzare una simulazione più dignitosa e ottenere gli stessi grafici, ma ha vinto la pigrizia.
Ho preparato quindi due fogli in LibreOffice Calc, ciascuno con un tabellone di 500 righe (i tentativi ripetuti) di 300 colonne (l’attesa massima che mi sono dato per ottenere l’esito “55” o “56”).
In ogni riga una semplice formula ripetitiva simula l’estrazione del dado, mediante la funzione CASUALE(), fino a che non venga rilevata la sequenza “55” in un foglio, “56” nell’altro.
Ecco l’esito di un’esecuzione di 500 tentativi di ciascun gioco:
Con sole 500 prove ripetute non potevo attendermi una precisione più elevata, ma il test conferma comunque il risultato atteso: 43,1 tiri in media per il gioco “55” (invece di 42), contro 37,4 del gioco “56” (invece di 36).
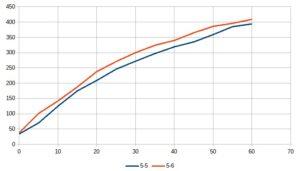
Che il secondo gioco consenta di raggiungere prima il traguardo si osserva meglio da questo grafico, che riporta il numero di prove ripetute con un risultato minore del valore ripotato sull’asse x. La curva del gioco “56” è un po’ più rapida nella salita.
Non si scivola solo sulla statistica dei dadi
Il caso riportato dall’articolo di Medium evidenzia come sia facile scivolare su una questione statistica e come, di conseguenza, la verità possa rivelarsi a volte sorprendente.
Un caso simile è quello del Paradosso di Monty Hall, riportato in un precedente articolo su Inchiostro Virtuale. Anche in quel caso ero scivolato con grande sicurezza nella falla del ragionamento statistico. Insomma, mai sentirsi troppo sicuri di sé, in questo campo.
La foto di apertura dell’articolo è di OpenClipart-Vectors da Pixabay. Il dado è sbagliato, ma la foto mi è piaciuta lo stesso.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.