Mente e acqua: un po' di ginnastica non guasta

Spero di non essere tacciato di futilità se, nel celebrare la Giornata mondiale dell’acqua, mi viene in mente il repertorio di quesiti logico-matematici che legano mente e acqua, sia essa quella di mari, fiumi, piscine, o anche un semplice rubinetto. Vediamone insieme qualcuno.

Mente e acqua: un problema di galleggiamento

Cominciamo dalle piscine. Diversi anni fa, sul sito Freepuzzles.com trovai questo quesito:

In piscina una tavoletta galleggia in acqua. Cosa farà alzare di più il livello dell’acqua: appoggiare una moneta da un euro sulla tavoletta o lasciar cadere la stessa moneta in acqua?

Se ci si ricorda del principio di Archimede, trovare la soluzione dovrebbe essere semplice. Una moneta completamente immersa sposta un volume di acqua pari al proprio volume; se invece è appoggiata sulla tavoletta galleggiante…

Aiuto, una bionda in mare!

Lo so, dovrebbe essere “un uomo in mare”, ma la bionda mi comunica una maggiore urgenza di salvataggio.
Allora: siamo sul trespolo in mezzo alla spiaggia e, da bravi bagnini, scrutiamo l’orizzonte. A qualche decina di metri dalla riva, spostata sulla destra, una bionda annaspa nell’acqua e agita le braccia cercando di richiamare la nostra attenzione.

Un balzo e siamo giù dal trespolo. Qual è la strada più veloce per raggiungere la fanciulla, tenendo conto che siamo più veloci a correre sulla sabbia che a nuotare? Bisogna ragionarci, è un caso classico di mente e acqua.

Verrebbe istintivo scegliere tra:

rendere minimo il percorso, puntando dritti verso la bionda, correndo sulla sabbia finché si può e poi proseguendo a nuoto;
cercare di nuotare il meno possibile, quindi correndo dritti sulla sabbia fino al punto della battigia da cui si vede la bionda sulla perpendicolare.

Ebbene, il percorso più veloce è intermedio tra i due. Avendo seguito proficuamente il corso di fisica, e ricordando alla perfezione la legge di Snell, sappiamo che il percorso ottimale sarà una linea spezzata simile a quella di un raggio di luce puntato in acqua.
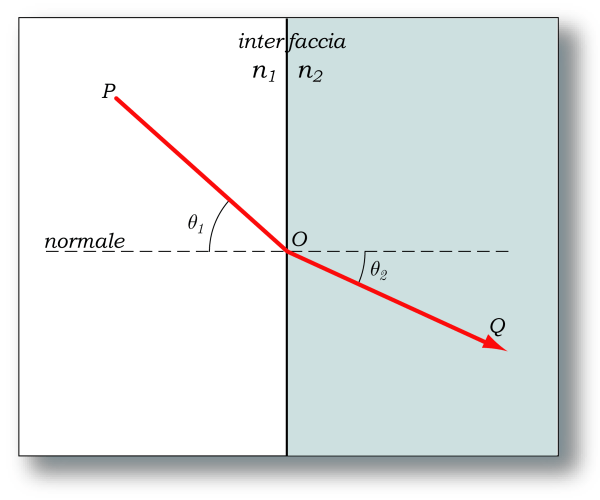
Se, nell’illustrazione in basso P è la posizione iniziale del bagnino e Q quella della fanciulla, allora come indici di rifrazione n₁ e n₂ possiamo considerare il reciproco della nostra velocità, rispettivamente sulla sabbia e in acqua.

Gli angoli θ₁ e θ₂ che descriveranno la nostra traiettoria, saranno allora dati dall’equazione:

n₁ sen θ₁ = n₂ sen θ₂

La funzione “sen” sta per il seno dell’angolo, e non fa assolutamente alcun riferimento alla fanciulla.

Legge di snell, mente e acqua — Da Wikipedia.

Mente e acqua: magie al rubinetto

Devo dire che l’ottica, insieme alla termodinamica, è uno degli argomenti dei corsi di Fisica che mi ha preso meno, e di cui ho un ricordo lacunoso. La legge di Snell mi era però rimasta in mente, perché la rifrazione di un raggio di luce in acqua è qualcosa di pratico, con cui ci si può ritrovare a giocare a mare in un momento di noia.
Se, però, è complicato spiegare a un ragazzino la legge di Snell, ci sono altri esperimenti da fare in casa di sicuro effetto sui ragazzi.
Esempio: facciamo scorrere un filo d’acqua da un rubinetto (più il filo è sottile e continuo, meglio è) e avviciniamo una penna che avremo prima strofinato con un panno (meglio se di lana). Magia!

Una passeggiata sui ponti di Königsberg

Il problema è arcinoto. Nella città prussiana di Königsberg (oggi Kaliningrad, enclave russa in Polonia), il fiume Pregel forma due isole prima di sfociare nel mar Baltico. A metà del ‘700, le due isole erano collegate alla terraferma da sette ponti. La leggenda vuole che una degli svaghi diffusi in città fosse quello di trovare un percorso che attraversasse, una sola volta, tutti e sette i ponti. In azione mente e acqua, quindi.

Il problema fu affrontato e risolto da Eulero, in uno dei primi ragionamenti sulla teoria dei Grafi.

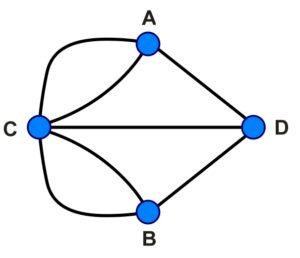
Il colpo di genio del matematico svizzero consistette nel rappresentare in maniera diversa il problema, rimpiazzando le due isole e le due sponde sulla terra ferma con quattro punti, e i ponti con linee che congiungevano i punti stessi.

Nell’immagine: C è l’isola a sinistra, D quella a destra, A la sponda superiore e B quella inferiore.

Il problema si riconduce quindi a percorrere il grafo, passando una sola volta per ogni linea.
Ora contiamo quante linee afferiscono a ciascun punto:

A, 3 linee;
B, 3 linee;
C, 5 linee;
D, 3 linee;

La linea che cerchiamo dovrà partire da un punto, terminare su un altro (o eventualmente lo stesso) ed entrare e uscire dagli altri punti.
Quindi solo due punti (quello iniziale e quello finale) possono avere un numero dispari di linee afferenti, gli altri punti devono averne in numero pari.

Quindi, concluse Eulero, il problema non ha soluzione.

A proposito di ponti: cliccate qui, per leggere l’articolo sui ponti naturali più suggestivi,
e qui, per leggere quello sui ponti artificiali più celebri!

Prendiamo la mano con i grafi

Chi non ricorda la casetta in alto a sinistra nella figura a lato? 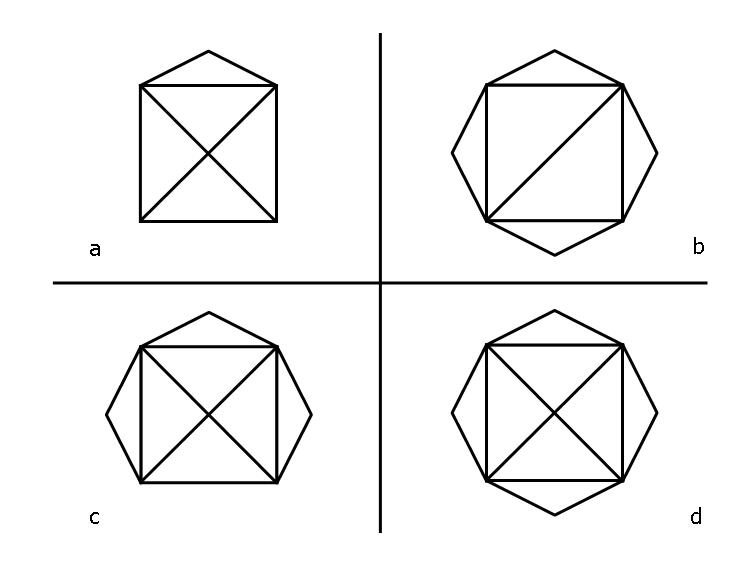Immagino ci siamo passati tutti, alle elementari o alle medie: disegnare la casetta senza staccare la matita dal foglio, e senza ripassare mai due volte sullo stesso lato.

Proviamo ad applicare il ragionamento di Eulero ai quattro disegni della figura. Accanto a ogni vertice scriviamo quindi il numero di lati afferenti.
Per la casetta di scolastica memoria, partendo dal vertice in basso sinistra e procedendo in senso orario, si ha: 3, 4, 2, 4, 3.
Quindi, sì, ricordate bene, il percorso esiste e prevede di partire dal vertice in basso a sinistra (n=3) e terminare in quello in basso a destra (n=3). O viceversa, naturalmente. Gli altri tre vertici (n=4, oppure n=2) sono solo di passaggio.

E per gli altri tre disegni? Due sono possibili, uno no (quale?)

Il labirinto di Theoni Pappas

A metà degli anni ’80 il lavoro mi ha portato per brevi periodi negli Stati Uniti, a Cupertino, dove l’Olivetti Advanced Technology Center era dirimpettaio di una neonata Apple.
In una libreria lì intorno trovai un calendario, con un quiz matematico per ogni giorno dell’anno. Scoprii così l’autrice, Theoni Pappas, insegnante di matematica ed efficace divulgatrice.

In tempi più recenti ho acquistato il suo libro Le gioie della matematica, in cui un paio di pagine sono dedicate ai punti di Königsberg, e le due successive ai grafi.
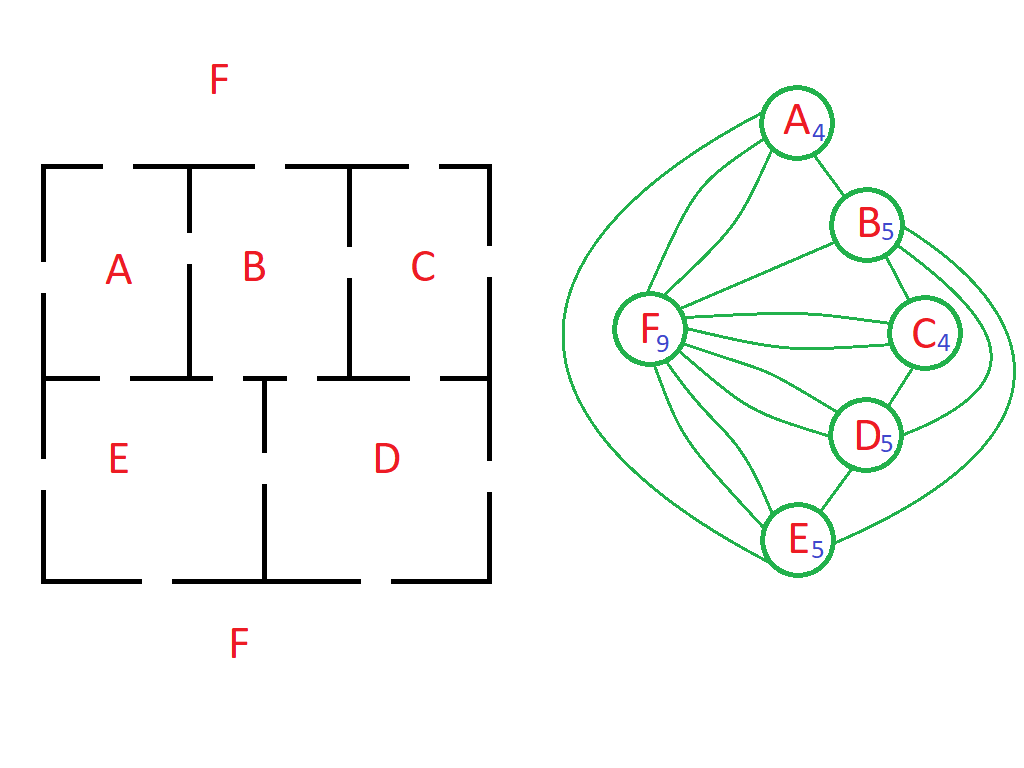In chiusura la Pappas propone di capire se nel labirinto rappresentato in figura sia possibile un percorso che porti ad attraversare ogni porta una sola volta.

Accanto al labirinto ho riportato il grafo relativo. Il punto F rappresenta il “fuori”, assumendo che una volta uscita da una delle stanze verso l’esterno, si possa rientrare da una qualunque delle porte che danno sull’esterno.

Applichiamo allora il nostro metodo deduttivo (mente e acqua, anche se di acqua non ce n’è).
Ci sono ben 4 nodi dispari, quindi la risposta immediata è no, niente percorsi.

Sarebbe però interessante capire se è possibile chiudere delle porte affinché il percorso cercato sia realizzabile.

Chiudete quella porta!

Quale effetto ha sul grafo la chiusura di una porta?
La porta tra le stanze D ed E è rappresentata nel grafo dalla linea che unisce i punti D (n=5) ed E (n=5).
Chiudere questa porta vuol dire eliminare la linea relativa dal grafo, e portare il conteggio dei due nodi a n=4.

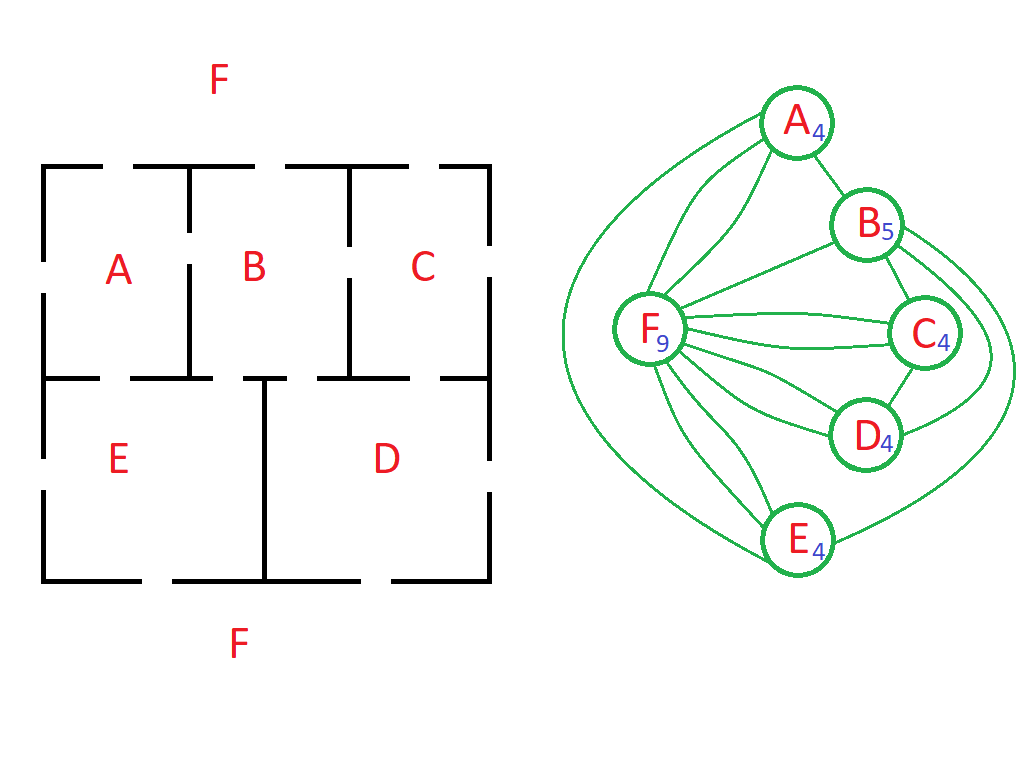Quindi (figura a lato), questa volta un percorso esiste e ha come estremi la stanza B e l’esterno del labirinto, punto F. Non so se esiste una soluzione unica, se volete dare un’occhiata a quella che ho trovato io, è qui.

Cosa accade se si chiude un’altra porta?

Se la porta unisce due punti pari, li rende dispari e quindi rende impossibile tracciare il percorso cercato, perché avremmo di nuovo 4 punti dispari.

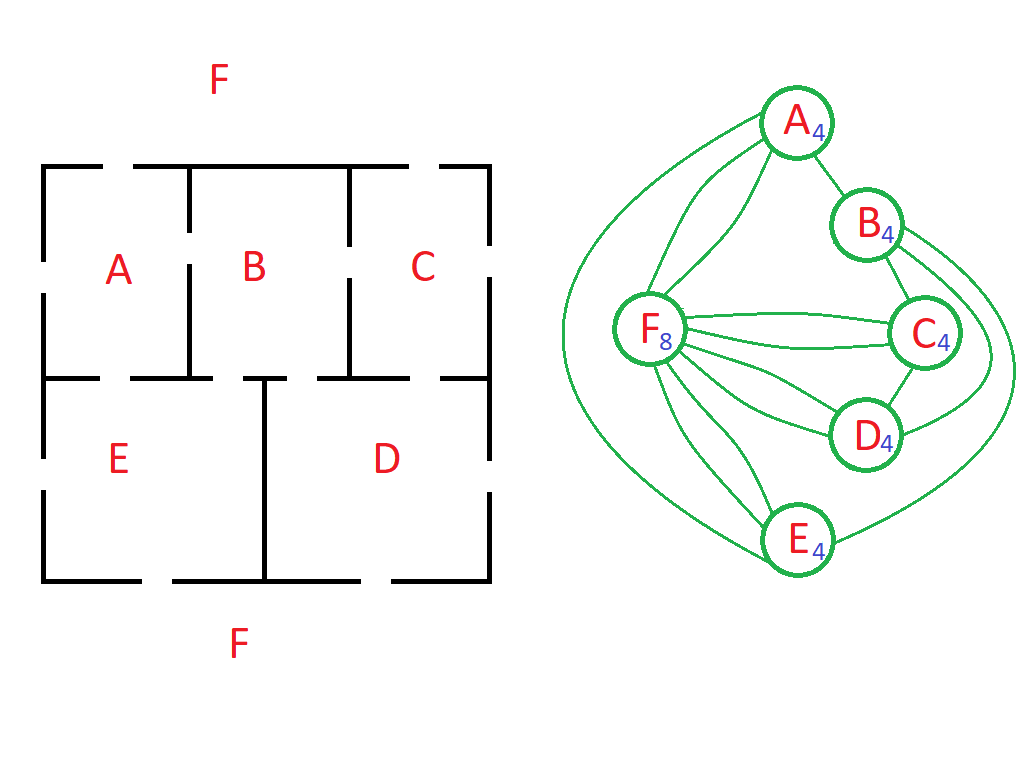Se, invece, la porta unisce i due punti dispari (F e B), allora chiuderla li rende pari.

A questo punto tutti i punti del grafo sono pari e, quindi, non ci saranno punti distinti di inizio e fine, ma il percorso sarà chiuso.

Nella figura a lato si è chiusa la porta che dalla stanza B dà sull’esterno.

Se non trovate il percorso, qui è visibile il mio. Essendo il percorso chiuso, cioè che parte e termina nella stessa stanza, ce ne saranno altri 5 equivalenti, scegliendo una tra le altre 4 stanze, oppure facendo partire e terminare il percorso all’esterno del labirinto (peraltro il problema è più estetico così).

Mente e acqua, ma non solo. Porsi delle sfide mentali è una ginnastica che accompagna il genere umano. Perché di questo si tratta, quando ci si pone una domanda che non ha ricadute pratiche visibili, ma serve solo a fissare una meta, divertendosi nel viaggio.