Il matematico britannico Henry Dudeney (10 aprile 1857–23 aprile 1930) è stato autore di una miniera di puzzle logici, raccolti in numerosi libri; celebre è il suo The Canterbury Puzzles.
Uno dei suoi rompicapo più noti, riportato ad esempio da Martin Gardner negli Enigmi e giochi matematici, è l’enigma ferroviario Smith-Jones-Robinson.
Capostipite dei giochi logici (niente calcoli, solo deduzioni), questo rompicapo può essere risolto con carta e matita, oppure al pc, con un semplice programma esaustivo. Un’occasione per conoscere meglio Ruby, uno dei linguaggi di programmazione più leggibili e potenti.
L’enigma ferroviario di Dudeney
In più di un secolo di vita, il rompicapo di Dudeney è stato presentato in varie forme. Il Guardian lo ha pubblicato nella versione britannica (vedi puzzle n.ro 5, qui la soluzione), molto vicina all’originale di Dudeney. Un’altra forma del rompicapo è riportata sul sito di puzzle logici Braingle.com. Quella che segue è la versione riportata da Martin Gardner, probabilmente la più nota.
| L’enigma ferroviario di Henry Dudeney |
|---|
|
Smith, Jones e Robinson sono l’ingegnere, il frenatore e il fuochista di un treno, ma non sono elencati esattamente in quest’ordine. Sul treno vi sono tre passeggeri con gli stessi tre nomi, identificati nelle premesse seguenti mediante un «Sig.» anteposto ai nomi.
Chi è l’ingegnere? |
Come si attacca il rompicapo?
Il metodo più diffuso, ben noto a chi frequenta la Settimana Enigmistica, si basa sulla costruzione di tabelle su cui annotare le inclusioni/esclusioni dedotte dal testo del rompicapo.
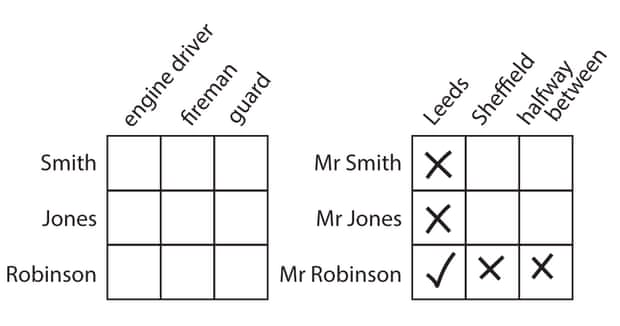 Per l’enigma ferroviario bastano due tabelle, come riportato da Martin Gardner. Per lasciare un margine alla sfida, riporto l’immagine proposta dal Guardian per la versione britannica del puzzle.
Per l’enigma ferroviario bastano due tabelle, come riportato da Martin Gardner. Per lasciare un margine alla sfida, riporto l’immagine proposta dal Guardian per la versione britannica del puzzle.
La prima tabella incrocia nomi e ruoli dei ferrovieri, l’altra nomi e località di residenza dei passeggeri.
Per risolvere il puzzle occorre tradurre le condizioni espresse dal testo in inclusioni (segno di spunta) o esclusioni (croce), fino ad avere un segno di spunta e due esclusioni nella prima colonna della tabella di sinistra, identificando così l’ingegnere.
L’approccio con il pc e Ruby
La velocità e la precisione di un programma elettronico consentono di utilizzare il metodo meno intelligente che si possa immaginare: elencare tutte le combinazioni possibili tra nomi, mansioni e luoghi, ed eliminare poi quelle in contraddizione con il testo. Ciò che rimane è la soluzione dell’enigma ferroviario.
Il linguaggio Ruby si presta a codificare in modo molto stringato ma comprensibilissimo questo tipo di algoritmi (vedi altri esempi su Inchiostro Virtuale).
La base è costituita dagli Array (o vettori) e dai relativi metodi.
Qualche semplice esempio:
- Array(1..90) costruisce un array con i numeri da 1 a 90;
- tombola = Array(1..90).shuffle dà una scrollata all’array e mette il risultato nella variabile tombola;
- a questo punto tombola[5] è, ad esempio, il quinto estratto.
L’espressione “.shuffle” è un metodo che, applicato all’oggetto array, lo modifica in una permutazione casuale dei suoi termini.
E se volessimo generare tutte le possibili permutazioni? Basterebbe ricorrere al metodo “.permutation” che, appunto, genera tutte le permutazioni possibili. Per elaborare ciascuna permutazione si può ricorrere a uno dei loop forniti da Ruby:
...
tombola = Array(1..90)
tombola.permutation.each do |tombolata_n|
elabora la tombolata N
end
... continua l'elaborazione del programma
Piccolo dettaglio: andrebbero generate (ed elaborate) 90! ≅ 1.49 × 10138 permutazioni. E anche con solo 1 millisecondo speso per ogni giro, è meglio desistere.
Come lavorare con Ruby
Ruby è un linguaggio a oggetti scritto nel 1993 dal giapponese Yukihiro Matsumoto, molto diffuso per scrivere applicazioni web.
Diversi tutorial e manuali sono disponibili sul web. Oltre al tutorial fornito dal sito istituzionale, è infatti disponibile la guida completa di Html.it, ma anche diverse guide pdf pubblicate in ambiente universitario, come ad esempio questa.
Una volta installato Ruby in ambiente Windows, si hanno a disposizione due finestre stile DOS. La prima è semplicemente un prompt di DOS che consente di utilizzare Ruby in modalità interattiva.
L’altra finestra è ancora un prompt di DOS, con l’ambiente run time di Ruby. Basta digitare il nome del file sorgente e INVIO per lanciarne l’esecuzione. Nell’immagine si vede, ad esempio, come lanciare il programma del puzzle di Dudeney, con stampa dei risultati in un file:
dudeney-puzzle.rb > dudeney-puzzle.txt
Per editare i file sorgente va bene un qualunque test editor. Il mio preferito in ambiente Windows è Notepad++ (l’immagine ne mostra una schermata). L’interfaccia riconosce il linguaggio e consente di comprimere o espandere la visualizzazione, rendendo più agevole l’editing di programmi anche complessi.
Gli Array nell’enigma ferroviario
Per risolvere il rompicapo, si parta dal definire questi array, definiti per elencazione degli elementi:
ferrovieri = ["Smith", "Jones", "Robinson"] passeggeri = ["Smith", "Jones", "Robinson"] mansioni = ["ingegnere", "frenatore", "fuochista"] luoghi_ferr = ["LosAngeles", "Omaha", "Chicago"] luoghi_pass = ["LosAngeles", "Omaha", "Chicago"]
Senza perdere di generalità, si possono fissare i primi due e considerare tutte le possibili permutazioni degli altri 3. Quindi si dovranno elencare ed esplorare 3! × 3! × 3! = 6 × 6 × 6 = 216 permutazioni:
mansioni.permutation.each do |ferr_mans|
luoghi_ferr.permutation.each do |ferr_luogo|
luoghi_pass.permutation.each do |pass_luogo|
[... qui vanno inserite le esclusioni ...]
[ ... se si arriva qui, è una soluzione! Stampala ...]
end
end
end
[... chiusura del programma ...]
Traduzione del testo in righe di programma
La prima condizione da rispettare è:
Il Sig. Robinson vive a Los Angeles.
Che si traduce in:
salta tutte le permutazioni in cui il sig. Robinson non vive a Los Angeles.
Per farlo costruiamo una funzione, in modo da isolare il relativo codice, migliorando la lettura del programma stesso:
def cond_1?(uno, val_uno, due, val_due)
(0..3).any? do |i|
uno[i] == val_uno && due[i] == val_due
end
Il nome della funzione (cond_1?) termina con un punto interrogativo, per convenzione stilistica di Ruby, comunicando visivamente che la funzione dovrà restituire un sì o un no, un VERO o FALSO.
In particolare restituirà VERO (o sì) se e solo se almeno un elemento dell’array uno[] sarà uguale a val_uno e il corrispondente elemento dell’array due[] sarà uguale a val_due.
La funzione può ora essere richiamata nel corpo dell’elaborazione, per tradurre la prima condizione dell’elenco:
Il Sig. Robinson vive a Los Angeles:
next unless cond_1?(passeggeri, "Robinson", pass_luogo, "LosAngeles")
Ovvero: salta questa permutazione ([go to] next) a meno che (unless) il passeggero Robinson non abiti a Los Angeles.
La stessa funzione può essere immediatamente riutilizzata per tradurre la seconda condizione:
Il frenatore vive a Omaha:
next unless cond_1?(ferr_mans, "frenatore", ferr_luogo, "Omaha")
E l’ultima:
Smith batte il fuochista al biliardo:
next if cond_1?(ferrovieri, "Smith", ferr_mans, "fuochista")
In quest’ultimo caso si utilizza “if” e non “unless“, perché occorre scartare le permutazioni in cui la funzione restituisce “VERO“, cioè quelle in cui Smith è il fuochista.
Quante permutazioni resistono a queste prime tre condizioni? Dalle 216 iniziali si scende a 72 applicando solo la prima e a 144 applicando solo ciascuna delle altre due. E solo 16 rimangono in gioco applicando tutte e tre le condizioni.
E ora tocca alle due condizioni più complicate
Le due condizioni:
Il Sig. Jones ha da parecchio tempo dimenticato tutta l’algebra imparata alle scuole superiori e: Il frenatore e uno dei passeggeri, un eminente fisico matematico, frequentano la stessa chiesa
sono da affrontare insieme.
Il Sig. Jones non è evidentemente un fisico matematico. Inoltre quest’ultimo abita nella stessa città del frenatore. Quindi le due condizioni possono essere tradotte in:
escludi la permutazione, a meno che il frenatore non abiti nella stessa
città di un viaggiatore che non è il Sig. Jones. Cioè:
next unless cond_2?(passeggeri, "Jones", ferr_mans, "frenatore",
pass_luogo, ferr_luogo)
def cond_2?(uno, val_uno, due, val_due, tre, quattro)
(0..3).any? do |i|
(0..3).any? do |j|
uno[i] != val_uno && due[j] == val_due && tre[i] == quattro[j]
end
end
end
Questa condizione da sola lascia in campo 144 permutazioni. In combinazione con le tre già viste ne lascia solo 8.
E ora l’ultima condizione
L’ultimo punto da coprire per risolvere l’enigma ferroviario è questo:
Il passeggero che ha lo stesso nome del frenatore vive a Chicago.
Analogamente al punto precedente:
next unless cond_3?(passeggeri, ferrovieri, ferr_mans, "frenatore",
pass_luogo, "Chicago")
dove:
def cond_3?(uno, due, tre, val_tre, quattro, val_quattro)
(0..3).any? do |i|
(0..3).any? do |j|
uno[i] == due[j] && tre[j] == val_tre && quattro[i] == val_quattro
end
end
end
Da sola, questa condizione lascia in campo 72 soluzioni, mentre in combinazione con tutte le altre ne lascia solo due:
ferrovieri: ["Smith", "Jones", "Robinson"] ["ingegnere", "frenatore", "fuochista"] ["LosAngeles", "Omaha", "Chicago"] passeggeri: ["Smith", "Jones", "Robinson"] ["Omaha", "Chicago", "LosAngeles"] ferrovieri: ["Smith", "Jones", "Robinson"] ["ingegnere", "frenatore", "fuochista"] ["Chicago", "Omaha", "LosAngeles"] passeggeri: ["Smith", "Jones", "Robinson"] ["Omaha", "Chicago", "LosAngeles"]
In grassetto nero sono marcate le differenze tra le due soluzioni, che riguardano la città di residenza dei signori Smith e Robinson. In ogni caso, l’ingegnere è Smith!
Il programma completo
# risoluzione di un puzzle di Dudeney (enigma ferroviario) # by p.p. - aprile 2018 # ferrovieri = ["Smith", "Jones", "Robinson"] passeggeri = ["Smith", "Jones", "Robinson"] mansioni = ["ingegnere", "frenatore", "fuochista"] luoghi_ferr = ["LosAngeles", "Omaha", "Chicago"] luoghi_pass = ["LosAngeles", "Omaha", "Chicago"] # def cond_1?(uno, val_uno, due, val_due) (0..3).any? do |i| uno[i] == val_uno && due[i] == val_due end end def cond_2?(uno, val_uno, due, val_due, tre, quattro) (0..3).any? do |i| (0..3).any? do |j| uno[i] != val_uno && due[j] == val_due && tre[i] == quattro[j] end end end def cond_3?(uno, due, tre, val_tre, quattro, val_quattro) (0..3).any? do |i| (0..3).any? do |j| uno[i] == due[j] && tre[j] == val_tre && quattro[i] == val_quattro end end end # n_sol = 0 t0 = Time.now mansioni.permutation.each do |ferr_mans| luoghi_ferr.permutation.each do |ferr_luogo| luoghi_pass.permutation.each do |pass_luogo| next unless cond_1?(passeggeri, "Robinson", pass_luogo, "LosAngeles") next unless cond_1?(ferr_mans, "frenatore", ferr_luogo, "Omaha") next unless cond_2?(passeggeri, "Jones", ferr_mans, "frenatore" pass_luogo, ferr_luogo) next unless cond_3?(passeggeri, ferrovieri, ferr_mans, "frenatore", pass_luogo, "Chicago") next if cond_1?(ferrovieri, "Smith", ferr_mans, "fuochista") print "ferrovieri:\n\t",ferrovieri, "\n\t", ferr_mans, "\n\t", ferr_luogo, "\n" print "passeggeri:\n\t", passeggeri, "\n\t", pass_luogo, "\n---\n" n_sol += 1 end end end print "\ntrovate ", n_sol, " soluzioni, in ", (1000*(Time.now - t0)).round(2), " msec\n"
L’ottimizzazione del codice
L’esecuzione del programma è molto veloce (meno di 15 msec sul mio pc), non ci sarebbe quindi una stretta necessità di ottimizzare il codice, pignoleria a parte.
Quali interventi si possono fare?
Si può innanzitutto sostituire le “print” con l’altra istruzione di stampa “puts“. Non ho trovato sul web riferimenti alla velocità delle due funzioni, ma devo dedurre che lo scambio sia efficace, visto che il tempo di esecuzione scende e si assesta intorno ai 5 msec.
puts "ferrovieri:\n\t #{ferrovieri} \n\t #{ferr_mans} \n\t #{ferr_luogo} \n"
puts "passeggeri:\n\t #{passeggeri} \n\t #{pass_luogo} \n---\n"
Puts stampa un’unica stringa, quindi gli elementi variabili devono essere trasformati in testo, mediante “#{…}“.
Un’ulteriore verifica si può effettuare commentando le righe dei criteri di esclusione (inserire “#” a inizio riga). In questo modo si stampano tutte e 216 le combinazioni, confermando la riduzione dei tempi di esecuzione di almeno 3:1.
Il secondo intervento riguarda la logica di generazione delle permutazioni.
Invece di verificare i criteri di esclusione dopo aver generato l’intera combinazione di permutazione, si può verificare ogni criterio non appena generato le permutazioni necessarie. Ad esempio:
[...]
luoghi_pass.permutation.each do |pass_luogo|
next unless cond_1?(passeggeri, "Robinson", pass_luogo, "LosAngeles")
mansioni.permutation.each do |ferr_mans|
[...]
Aver anticipato la verifica delle riga “next” risparmia la generazione delle permutazioni delle variabili successive, in tutti i casi di esclusione della permutazione.
Codice ottimizzato
Dopo aver riorganizzato in modo più efficiente la generazione delle permutazioni e i criteri di verifica, il codice del programma cambia in:
# risoluzione di un puzzle di Dudeney - versione ottimizzata # by p.p. - aprile 2018 # ferrovieri = ["Smith", "Jones", "Robinson"] passeggeri = ["Smith", "Jones", "Robinson"] mansioni = ["ingegnere", "frenatore", "fuochista"] luoghi_ferr = ["LosAngeles", "Omaha", "Chicago"] luoghi_pass = ["LosAngeles", "Omaha", "Chicago"] # def cond_1?(uno, val_uno, due, val_due) (0..3).any? do |i| uno[i] == val_uno && due[i] == val_due end end def cond_2?(uno, val_uno, due, val_due, tre, quattro) (0..3).any? do |i| (0..3).any? do |j| uno[i] != val_uno && due[j] == val_due && tre[i] == quattro[j] end end end def cond_3?(uno, due, tre, val_tre, quattro, val_quattro) (0..3).any? do |i| (0..3).any? do |j| uno[i] == due[j] && tre[j] == val_tre && quattro[i] == val_quattro end end end # n_sol = 0 t0 = Time.now luoghi_pass.permutation.each do |pass_luogo| next unless cond_1?(passeggeri, "Robinson", pass_luogo, "LosAngeles") mansioni.permutation.each do |ferr_mans| next if cond_1?(ferrovieri, "Smith", ferr_mans, "fuochista") next unless cond_3?(passeggeri, ferrovieri, ferr_mans, "frenatore", pass_luogo, "Chicago") luoghi_ferr.permutation.each do |ferr_luogo| next unless cond_1?(ferr_mans, "frenatore", ferr_luogo, "Omaha") next unless cond_2?(passeggeri, "Jones", ferr_mans, "frenatore", pass_luogo, ferr_luogo) puts "ferrovieri:\n\t #{ferrovieri} \n\t #{ferr_mans} \n\t #{ferr_luogo} \n" puts "passeggeri:\n\t #{passeggeri} \n\t #{pass_luogo} \n---\n" n_sol += 1 end end end puts "\ntrovate #{n_sol} soluzioni, in #{(1000*(Time.now - t0)).round(2)} msec\n"
Per questo articolo ho tratto ispirazione da un analogo articolo pubblicato su Medium: Solving Einstein’s Riddle with Ruby. Come sempre, scrivere un articolo solleva molti più dubbi rispetto al semplice leggerne uno sullo stesso tema e, lungo la strada, si impara sempre qualcosa di nuovo. Provare per credere.
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.