Un paio di questioni semplici semplici

Un paio di giochini matematici, da usare come digestivi pasquali? Qui di seguito ne propongo due, uno geometrico, l’altro aritmetico.
Sono entrambe questioni semplici. La prima richiede un po’ di creatività, che è ancora complesso realizzare con strumenti informatici. Per la seconda è sufficiente ragionare in modo ordinato. Affrontarlo porta a qualche riflessione sulla scalabilità degli approcci algoritmici.

La prima delle questioni semplici: cinque cerchi, ma non olimpici

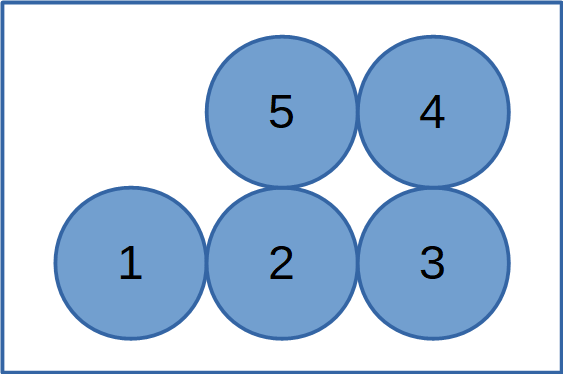Nella figura a lato sono riportati cinque cerchi uguali tra loro, disposti su due file tangenti, rispettivamente di due e tre cerchi.

Si chiede di tracciare una retta, che divida l’insieme dei cinque cerchi in due parti di uguale area.

La soluzione non è unica. Si potrebbe, ad esempio, tracciare una retta orizzontale, che tagli dai tre cerchi inferiori la giusta fetta da aggiungere ai due superiori. Sospetto che si debba far uso della formula per il calcolo dell’area del segmento circolare, e non sono esperienze piacevoli.

C’è però una soluzione semplice semplice, senza tirare in ballo calcoli complicati e il mitico pi-greco. Consiste nell’aggiungere qualcosa, che è poi ininfluente togliere. Una volta aggiunto questo qualcosa, la soluzione è sotto gli occhi. Per verificare se si è sulla strada giusta, basta dare un’occhiata qui.

Questioni semplici come questa possono essere affrontate in modo molto più efficiente dalla nostra mente, che non con un approccio informatico. Almeno fino a che non si ricorra agli strumenti dell’IA.

Contando gli zeri

La seconda delle questioni semplici riguarda la cifra zero.
Si scrivano i numeri da 1 a 1000 su un foglio di carta. Quante volte compare la cifra zero?

Un problema del genere si può approcciare in modi diversi, partendo dalla completa manualità, passando per l’aiuto del pc e terminando sull’utilizzo, nemmeno troppo spinto, del meraviglioso strumento che abbiamo nella testa.

Partiamo dal sistema manuale. Armati di carta, matita, tempo e pazienza, si esegue quanto chiesto, scrivendo i numeri da 1 a 1000, poi si contano gli zeri.
Un sistema del genere andrebbe bene se il conteggio fosse da eseguire per pochi numeri, mettiamo per quelli da 1 a 50. Oltre diventa noioso, oltre che prono all’errore. Detto in termini tecnici, è un metodo che non scala.

Il pc elimina la manualità!

Un foglio di calcolo (libre office, excel), poche formule e dieci minuti di tempo ci danno la risposta al problema.
Nella cella A1 inseriamo il numero 1 (il primo della lista) e nelle celle attigue inseriamo queste formule:

= TESTO(A1;”#”), nella cella B1
= SOSTITUISCI(B1;”0″;””), nella cella C1
= LUNGHEZZA(B1)-LUNGHEZZA(C1), nella cella D1

La logica è abbastanza semplice: prima trasformo il numero contenuto nella cella A1 in una stringa di testo, poi elimino dal testo gli eventuali zeri, infine calcolo quanti zeri ho eliminato.
Ora è sufficiente inserire nella prima colonna, a partire dalla seconda riga, i numeri da 2 a 1000. Con il riempimento automatico incrementale bastano pochi secondi. A questo punto le tre formule della prima riga vanno copiate all’ingiù, fino alla riga 1000.
Selezionando la colonna D si può leggere in fondo al foglio la somma delle celle, corrispondente agli zeri eliminati: 192.

Carta e matita sono sparite, la probabilità di errore è diminuita, visto che è un automatismo a sviluppare dati e formule. Ma il sistema non scala più di tanto: e se dovessimo contare gli zeri contenuti nei numeri da 1 a 10.000 ?

L’informatico è un narcisista

La razionalità dovrebbe portare a scrivere linee di codice, formule, algoritmi in modo che sia semplice capire come funzionano. Poco importa se il risultato non è il più compatto possibile, conta di più che il funzionamento di quanto si è realizzato, rimanendo sufficientemente efficiente, sia facilmente comprensibile anche da altri. Senza dimenticare che anche chi l’ha realizzato potrebbe in seguito dimenticare le finezze messe in campo.

Detto questo, spazio al narcisista che è in me, perché anche sulle questioni semplici si possono inserire complicazioni a volontà.
Il problema si può risolvere con un’unica formula nella cella A1, estesa poi fino alla cella 1000:

= LUNGHEZZA(TESTO(RIF.RIGA(A1);”#”)) – LUNGHEZZA(SOSTITUISCI(TESTO(RIF.RIGA(A1);”#”);”0″;””))

Il funzionamento è lo stesso, l’unica sostanziale differenza è l’utilizzo della funzione RIF.RIGA(A1) che, una volta estesa in giù, compila in modo automatico i numeri da 1 a 1000. Ho solo reso oscuro il tutto, il metodo continua a non scalare, ma ho compresso tutto in una sola formula. Non è bellissimo?

Scriviamo un programmino

Excel ha il vantaggio di essere semplice da utilizzare. Per contro non sempre si adatta alle dimensioni del problema da risolvere. Ed è qui che viene in aiuto la programmazione.

Utilizzando Ruby, uno dei linguaggi più vicini al linguaggio naturale (inglese, ovviamente) il problema si risolve così (con Ubasic il programma sarebbe stato un po’ meno leggibile):

# quanti zeri ci sono nei numeri da 1 a 1000?
#
range = (1..1000)
zeri = 0
range.each do |n|
zeri += n.to_s.length – n.to_s.gsub(“0″,””).length
end
print “Nei numeri nel range “,range,” compaiono “, zeri, ” zeri”

Il programma calcola quanto richiesto e infine stampa a video il risultato:

Nei numeri nel range 1..1000 compaiono 192 zeri

Abbiamo realizzato un notevole passo in avanti. Una piccola modifica al range:

range = (1..10000)

e possiamo calcolare gli zeri utilizzati per scrivere i numeri da 1 a 10.000:

Nei numeri nel range 1..10000 compaiono 2893 zeri

Il metodo scala decisamente meglio. Mi manca però il coraggio di verificare se è corretto. Mi fido.

E se ci ragionassimo un po’ su?

Lasciamo da parte fogli di calcolo e programmazione, ritorniamo al metodo manuale, ma questa volta ragioniamo prima di sprecare carta e matita.
Invece di riportare effettivamente i numeri da 1 a 1000, ipotizziamo di riportare i numeri da 0 a 999 secondo uno schema ordinato. Per ottenere il risultato giusto, alla fine basterà togliere 1 (lo 0 iniziale) e aggiungere 3 (il 1000 finale).

Dividiamo i 1000 numeri in dieci blocchi da 100, e scriviamo ogni blocco su 10 righe da 10 numeri ciascuno.
Il primo blocco ha 10 zeri, uno per ciascun primo elemento di riga:

0, 1, …, 9
10, 11, …, 19
…
90, 91, …, 99

I 9 blocchi successivi hanno ciascuno 20 zeri, di cui 10 sono le decine nella prima riga, gli altri 10 sono le unità nella prima colonna:

100, 101, …, 109
110, 111, …, 119
…
190, 191, …, 199

A questo punto il calcolo è semplice:

10 + 9 * 20 – 1 + 3 = 192

Quanto scala la mente?

Abbiamo visto due questioni semplici in sé. La prima, i cinque cerchi, in cui è rilevante ragionare sulla forma di oggetti, e ragionare sulle simmetrie. La seconda, al contrario, riportabile a semplici modelli matematici.

Sul primo tipo di problemi la mente non ha ancora rivali praticabili. Sul secondo l’approccio informatico corretto prevale non appena sia in ballo una dimensione ampia del problema.

Almeno per i numeri da 1 a 1000, infatti, la mente batte il pc. Per quest’ultimo, infatti, va messo in conto il tempo per organizzare il foglio di calcolo o il programma.
Se invece portiamo a 10.000 il limite superiore, beh, gli occhi si incrociano mentre si mette giù lo schema della divisione in blocchi dei numeri, e il rischio di commettere errori aumenta.
D’altro canto, il foglio di calcolo diventa difficilmente praticabile, mentre il programma si adatta in un attimo e completa la sua esecuzione rapidamente.
Con un limite superiore di 100.000, non c’è storia, il programma Ruby è il solo dei metodi visti a portare a casa il risultato.

Sempre che non si trovi un ragionamento più scalabile!