Matematica in fumo: sigarette, sigari, pipe e fiammiferi

Matematica in fumo, ma in realtà c’è fumo e fumo: sigaretta, sigaro, pipa, e alla matematica lego solo quest’ultima.
La sigaretta mi dà il senso dell’ansia, dell’esilio (avete presente i fumatori di sigaretta al freddo invernale, fuori dalla porta dello stabile dell’ufficio, montagnetta di cicche in un angolo?).
E il sigaro mi comunicherebbe il piacere di una buona cena, se solo non mi desse fastidio l’odore penetrante.

Il rito della pipa, invece, concilia la riflessione. Quando è il momento, ti prendi una pausa e lasci le mani manovrare per caricare la pipa, mentre i pensieri provano a mettersi in ordine da soli. In genere funziona, dopo un po’ di boccate puoi cominciare a chiudere la pausa, ma con calma. Per chi fosse tentato, ecco un bell’articolo sulla pipa.
Ebbene sì, sono un (blando) fumatore di pipa, soltanto all’aperto (esempio, terrazzo di casa) e senza accentuata dipendenza.
Quindi, in occasione della Giornata Mondiale senza Tabacco, glisso. Non cerco assoluzioni, anche se in realtà ne ho appena abbozzato un tentativo, ma giro la questione sul gioco. Perché sigarette, sigari e pipa, oltre ai fiammiferi, sono oggetto di puzzle matematico-logici. Vediamone alcuni.

Matematica in fumo, cominciamo dai sigari

Per partire, un classico puzzle, dovuto a Henry Dudeney, già incontrato con l’enigma ferroviario. Il puzzle viene riportato, ad esempio, su Mathematical Elegance: An Approachable Guide to Understanding Basic Concepts.

Siete seduti al bar con un amico. In attesa che arrivino i caffè, sfidate il vostro amico a un gioco con i sigari della scatola (enorme) che avete appena comprato. A turno ognuno di voi posizionerà un sigaro sul tavolo, senza toccare nessun altro sigaro già posato. Perde chi non riesce a trovare un buco libero sul tavolo.
I sigari hanno forma cilindrica, con un estremo piatto e l’altro arrotondato, e ce ne sono a sufficienza per ricoprire il tavolo.

Esiste una strategia vincente per chi comincia o per il secondo a giocare?

Lasciamo una pausa di riflessione, la soluzione si trova al fondo dell’articolo.

Un altro puzzle logico, l’interrogatorio

Ancora per la serie della matematica in fumo, un divertente puzzle logico, riportato da Barry R. Clarke nel suo Challenging Logic Puzzles:

As Shaky Sheila entered the interview room, her four interrogators — Arbuthnot, Bounder, Cad, and Drat (one of whom was a non-smoker) — sat behind the oak table polishing their questions. Sheila mentally numbered them from one to four, left to right, and noted the following facts.

1) The pipe smoker sat immediately to the right of Bounder.
2) Cad did not smoke cigarettes.
3) The cigarette smoker sat immediately to the left of Arbuthnot.
4) Cad was not the cigar smoker.
5) The cigar smoker sat immediately to the left of the cigarette smoker.
6) The cigar smoker was neither second or third.

If no interrogator had two different smoking habits, can you find the name and smoking habit for each position?

Il gioco è analogo a quello visto per l’enigma ferroviario, quindi si può approcciare con gli stessi due metodi: carta e penna oppure un programmino al pc.
Dunque, la nostra traballante Sheila viene interrogata da quattro persone sedute al tavolo di fronte a lei, uno accanto all’altro. Dall’iniziale del nome possiamo indicarli con A, B, C e D, seduti in posizioni che lei stessa identifica, da sinistra a destra, con 1, 2, 3 e 4. Durante l’interrogatorio, uno dei quattro fuma una sigaretta, un altro un sigaro, un altro ancora la pipa. L’ultimo non fuma.

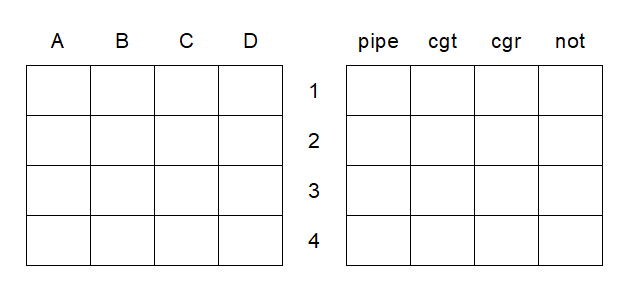L’approccio carta e penna parte da uno schema come quello riportato. Ciò che occorre fare è tradurre le condizioni del testo in esclusioni, fino a che rimanga solo la soluzione.

Un primo passo è riportato in questa figura. Un altro passetto si trova qui e, infine, ecco la soluzione.

Aggiungiamo una dimensione al gioco

Ricorrendo a un programma si sposta il divertimento, dalla sfida logica del gioco al piacere di scrivere il programma. In realtà, nello spirito della matematica in fumo, si può aggiungere una dimensione esplorativa, che sarebbe poco praticabile con carta e penna: esistono soluzioni (e quante) se si modificano in tutte le combinazioni possibili destra e sinistra nelle condizioni 1, 3 e 5?

Il programma Ruby, insieme alla stampa dei risultati si possono scaricare qui.

Oltre alla soluzione al problema originale:

c1 = dx, c3 = sx, c5 = sx:
[“Cad”, “Arbuthnot”, “Bounder”, “Drat”]
[“niente”, “pipa”, “sigaretta”, “sigaro”]

si trova la disposizione speculare:

c1 = sx, c3 = dx, c5 = dx:
[“Drat”, “Bounder”, “Arbuthnot”, “Cad”]
[“sigaro”, “sigaretta”, “pipa”, “niente”]

Una soluzione diversa (insieme a quella speculare) si trova con:

c1 = dx, c3 = sx, c5 = dx:
[“Arbuthnot”, “Drat”, “Cad”, “Bounder”]
[“sigaro”, “sigaretta”, “pipa”, “niente”]

C’è ancora una combinazione e la sua speculare che danno tre possibili soluzioni (vanificando quindi il gioco). Le restanti combinazioni non danno soluzioni.

E i fiammiferi?

Per attivare la matematica in fumo occorre anche accendere il fuoco.
Una gamma estesissima di puzzle è legata ai fiammiferi: partendo da una disposizione di alcuni fiammiferi, raggiungerne una diversa spostando un numero determinato di fiammiferi.

Ecco un esempio, cambiare direzione all’asinello, spostando un solo fiammifero:

La soluzione qui.

Altro esempio, spostare quattro fiammiferi, in modo da ottenere tre quadrati, dai due iniziali:

Soluzione qui.

Sigari sul tavolo, la soluzione!

Nel gioco dei sigari di Dudeney, riportato in apertura, il primo giocatore ha una strategia vincente, basata sulla simmetria.
Gli sarà sufficiente porre il primo sigaro in piedi, appoggiato sull’estremo piatto, al centro esatto del tavolo. Da questo momento, ad ogni sigaro posato dal secondo giocatore risponderà ponendo il suo in posizione simmetrica rispetto al centro del tavolo. Ovvio che troverà sempre modo di farlo, mentre il secondo giocatore, prima o poi, non troverà più spazio.

Fumate poco, sarebbe meglio niente. Ma se proprio vi va di farlo, viva la pipa!
E adesso, prima di rileggere il post, ci vuole una pausa, con la pipa ritratta nella foto di apertura.