Il termine Gaussiana è probabilmente noto anche a chi non è mai inciampato nello studio del calcolo delle probabilità. E se pure non evocasse nulla, quasi certamente sarà familiare la curva a campana della distribuzione statistica di Gauss e se ne conosce la caratteristica: i valori più comuni sono verso il centro della campana, quelli più rari agli estremi.
La funzione deve il suo nome al matematico, astronomo e fisico tedesco Carl Friedrich Gauss.
Conosciamo un po’ più da vicino Gauss e la Gaussiana, con l’aiuto di Excel.
Gauss, un bambino prodigio
Nato a Braunschweig il 30 aprile 1777 da una famiglia di modeste condizioni sociali, Carl Friedrich Gauss rivelò fin da bambino la sua propensione per la matematica. Nella storia del personaggio sono rimasti un paio di aneddoti al riguardo, di veridicità non confermata, ma che ben raccontano il piccolo Gauss.

Il primo: all’età di tre anni avrebbe corretto un errore commesso dal padre nei conti di casa. Il secondo, più credibile, risale invece ai banchi della scuola elementare ed esiste in varie versioni.
Quella più diffusa racconta che l’insegnante, per tenere occupata la classe, chiese di calcolare la somma dei numeri interi da 1 a 100. Pochi secondi e il piccolo Carl Friedrich annota sulla sua lavagnetta il risultato e la ripone a faccia in giù sul banco. Poi insegnante e allievo rimangono a fissarsi per tutto il tempo necessario al resto della classe per completare il computo.
Alla verifica, un solo risultato è corretto, quello di Gauss, calcolato a mente e in pochi secondi.
Come ha fatto? Gauss avrebbe ragionato così: suppongo di scrivere i numeri da 1 a 100 in fila e poi, incolonnati nella riga sottostante, scrivo i numeri da 100 a 1.
Bene: la somma di tutti i numeri scritti è il doppio del risultato richiesto; ognuna delle 100 coppie in verticale (1 e 100, 2 e 99, 3 e 98, … 99 e 2, 100 e 1) ha somma pari a 101. Quindi il risultato richiesto, semplice da ricavare a mente anche per me, è:
101 * 100 / 2 = 5.050
Se la Matematica è la Regina delle scienze, come lo stesso Gauss scrisse, i posteri hanno scelto lui come Principe dei matematici.
Pauca, sed matura
Che siano veri o meno i due aneddoti riportati, Johann Friedrich Gauss fu prolifico di risultati scientifici, che però rese noti solo quando fu in grado di provarne la correttezza, secondo il suo motto: Pauca, sed matura (poche cose, ma mature).
Iscritto a 18 anni all’università di Gottinga, su incoraggiamento della madre (il padre era invece contrario), ma soprattutto grazie alla sponsorizzazione degli insegnanti e del duca di Brunswick, a soli 19 anni raggiunse il primo risultato matematico significativo. Dimostrò infatti che ogni numero intero positivo si può scrivere come somma di non più di tre numeri triangolari.
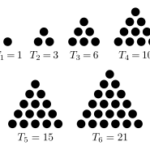
I numeri triangolari sono: 1, 1+2, 1+2+3, … Devono il nome alla rappresentazione grafica più naturale. Non sembrerà un risultato che ribalti le sorti dell’umanità, ma dimostra la capacità speculativa di Gauss, che fu così orgoglioso del risultato raggiunto da decidere di annotare in un diario i risultati raggiunti, cominciando proprio da questo:
Eureka! num = Δ + Δ + Δ
In 18 anni Gauss riportò nel diario 146 enunciati, talvolta in modo criptico (due, in particolare, sono rimasti incomprensibili). Le 19 pagine del diario, riportando la data per ogni annotazione, hanno consentito di stabilire la precedenza di Gauss su alcuni risultati mai resi pubblici, oppure pubblicati con ritardo.
Un cranio non comune
Era tale la fama di Gauss che, alla sua morte a quasi 78 anni, il 23 febbraio 1855, fu deciso di esaminarne il cervello per verificare se avesse qualche caratteristica particolare, a supporto della sua genialità.
L’analisi riportò 219.588 millimetri quadrati di area cerebrale per una massa di 1,492 grammi, decisamente abbondante e ricca di circonvoluzioni.
Gauss e l’astronomia
Oltre che matematico, Gauss fu un astronomo di successo.
Il 1° gennaio del 1801 l’italiano Giuseppe Piazzi aveva scoperto Cerere, il più grande oggetto che orbita nella fascia degli asteroidi, tra Marte e Giove. Classificato inizialmente come pianeta, poi declassato ad asteroide, dal 2006 Cerere è, con Plutone, un pianeta nano.
Cerere rimase visibile per poche settimane, prima di nascondersi dietro il sole. I dati sulla sua posizione erano davvero pochi, appena un grado di rotazione su 360, c’erano quindi poche speranze di ritrovarlo facilmente, una volta tornato visibile.
Un problema per molti, ma non per Gauss. Impiegando il metodo dei minimi quadrati, che applicava fin dal 1794, ma che rese pubblico solo nel 1809, Gauss riuscì in tre mesi di lavoro a determinare la posizione che Cerere avrebbe raggiunto in dicembre. Sbagliò di appena mezzo grado.
Gauss scopre la Gaussiana
Fu proprio effettuando misurazioni astronomiche che Gauss si trovò a fronteggiare il problema degli errori: ripetendo più volte la stessa misura, il risultato ottenuto presentava di volta in volta lievi variazioni. Come dedurre il valore più corretto della misura, e determinarne l’affidabilità?
Gauss notò che i valori ottenuti dalla misura si distribuivano addensandosi intorno a un valore centrale, e disperdendosi, sempre più radi, allontanandosi da questo valore.
Cercando una funzione che rappresentasse in modo efficace la distribuzione dei valori ottenuti, Gauss arrivò a questa:
e(x – µ)^2 / σ^2
in cui µ rappresenta il valore medio delle misure effettuate e σ^2 indica l’ampiezza della dispersione dei risultati (varianza). Questa distribuzione statistica viene chiamata distribuzione di Gauss o anche distribuzione normale.
Molti anni dopo, nel 1922, il matematico finlandese Jarl Waldemar Lindeberg diede un fondamento teorico al risultato di Gauss con il teorema del limite centrale: la somma di un numero infinito di variabili aleatorie con identica distribuzione tende ad assumere una distribuzione normale.
In parole semplici, ci troveremo di fronte a una distribuzione a campana tutte le volte che il fenomeno che osserviamo è soggetto a svariare variabili aleatorie, tutte con la stessa distribuzione statistica. È questo il caso degli errori di misura in cui si era imbattuto Gauss, ma anche, in prima approssimazione, il caso della statura umana: molti fattori indipendenti possono avere un contributo sulla crescita, l’effetto combinato distribuisce l’altezza finale sotto una campana di Gauss.
La Gaussiana ed Excel
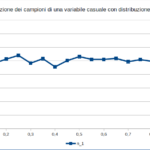
Possiamo simulare dei fenomeni casuali su Excel tramite la funzione casuale(), che restituisce un valore casuale tra 0 e 1, con distribuzione uniforme. Basterà inserire la formula = casuale() in un numero abbastanza grande di celle di una colonna (esempio: 10.000), per simulare i risultati di un esperimento con risultato casuale e distribuzione uniforme.
E se l’esperimento che vogliamo simulare fosse composto da più fenomeni aleatori? Basterà sommare più valori casuali nella stessa cella. Esempio:
= casuale() + casuale(), oppure:
= casuale() + casuale() + casuale()
e così via.
Per poter confrontare in modo corretto i vari casi, conviene normalizzare i valori massimi, quindi:
= (casuale() + casuale()) / 2,
= (casuale() + casuale() + casuale())/3
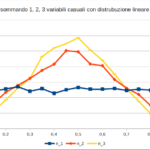
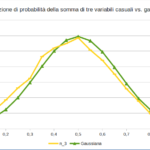
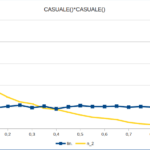
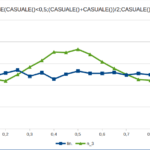
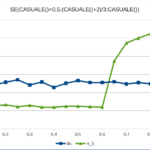
Nelle figure qui sotto sono riportate le distribuzioni su un campione di 10.000 esperimenti delle tre variabili aleatorie: singola variabile, somma di due e di tre variabili. Quest’ultimo caso è confrontato con la distribuzione Gaussiana con la stessa media e varianza. Il file Excel può essere scaricato da qui.
Come si vede, lo scostamento è, già con sole tre variabili, molto ridotto. Quindi non è necessario un numero molto elevato di fattori casuali combinati, perché la distribuzione finale si approssimi alla Gaussiana.
Non solo Gaussiana
L’utilizzo della funzione casuale() consente di costruire con Excel sequenze di dati casuali per studiare il comportamento di algoritmi.
Spesso, però, è necessario partire da distribuzioni diverse da quella uniforme, ma Excel non ha funzioni che diano direttamente questo risultato. È possibile però manipolare la distribuzione, come mostrato nelle rimanenti figure riportate.
In particolare si può giocare con la funzione ass(), che restituisce il valore assoluto dell’argomento.
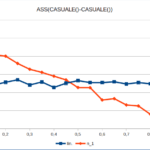
Così, se: “= casuale() – casuale()” restituisce una funzione distribuita tra -1 e 1, con distribuzione “triangolare”, allora: “= ass( casuale() – casuale() ) ribalta la metà negativa su quella positiva e consente di ottenere la distribuzione riportata nella figura gauss-6.
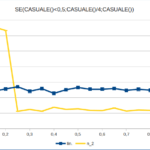
Altra leva disponibile: utilizzando la funzione “se(condizione, allora, altrimenti)“, si può utilizzare un primo valore casuale per decidere quale delle due scelte seguire, e combinare due diverse funzioni casuali (vedi figura gauss-7).
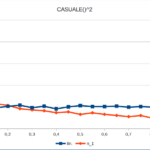
Notare che ogni utilizzo di casuale() genera un distinto valore. Quindi:
casuale()2, e
casuale() * casuale()
hanno comportamenti diversi (cfr. immagini gauss-4 e gauss-5). Inoltre, ad ogni modifica del file (esempio: modifica del contenuto di una cella), Excel assegna un nuovo valore casuale a ogni funzione casuale().
Ultima nota: il file è compatibile con LibreOffice Calc (in realtà è proprio con Calc che l’ho preparato).
Non rimane che scaricare il file e provare a giocare!
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.