Disegnare con il pc, utilizzando la search di google, excel e ancora altro

Disegnare con il pc è un modo efficace per mettere alla prova la creatività personale, anche per chi, come me, è un’autentica schiappa nel disegno a mano libera.
Scopriamo tre modi per farlo: un insolito e semplice utilizzo della calcolatrice integrata nelle ricerca di Google; il buon vecchio Excel (o LibreOffice Calc); e, per finire, un po’ di programmazione (per chi abbia voglia di cimentarsi).

---

Il modo più semplice per disegnare con il pc: la calcolatrice integrata nella ricerca di Google

Qualche anno fa Google ha inserito nel suo motore di ricerca la possibilità di tracciare grafici di funzioni, arricchendo così le possibilità di disegnare con il pc.

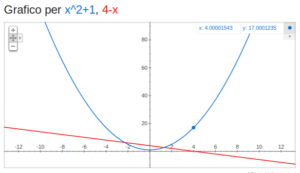
L’utilizzo è semplicissimo: basta digitare sulla pagina di ricerca di Google, al posto delle parole da ricercare, la funzione di cui si desidera visualizzare il grafico; ad esempio x^2 + 1 (tradotto: x² + 1, l’equazione di una parabola). Avviate la ricerca e… Fatto.
Per visualizzare il grafico di due o più funzioni basta inserire le rispettive espressioni separate da una virgola; ad esempio: x^2 + 1, 4 – x.

Nota: i numeri decimali vanno digitati con il punto decimale, e non con la virgola: 1.2 e non 1,2.

Come si vede da questi due esempi, l’estensione dell’asse orizzontale si adegua automaticamente. Nell’angolo in alto a sinistra ci sono comunque i bottoni per lo zoom dell’immagine, sia in orizzontale che in verticale.
È possibile anche impostare direttamente l’estensione dell’asse orizzontale; ad esempio: x^2 + 1, 4 – x from -6 to 6.
Ancora: con il puntatore del mouse all’interno del grafico, tenendo premuto il pulsante destro è possibile spostare il grafico stesso nella finestra.

Adesso bisogna aggiungere un po’ di creatività

Tracciare grafici direttamente dalla ricerca di Google farà felici gli studenti delle superiori, ma si presta anche a un simpatico giochino: inventare combinazioni di funzioni il cui grafico somigli da vicino a qualcosa. Occorre però aggiungere un pizzico di creatività.

Provate a tracciare la funzione sin(x). Si tratta della funzione Seno di un angolo, è custodita nel cassetto della memoria etichettato Trigonometria, terzo o quarto anno delle superiori, il mio ricordo si perde nella notte dei tempi. Bene, sin(x) va su e giù tra -1 e +1, e fin qui niente di nuovo. Si può però accelerare il ritmo di oscillazione così: sin(100x).

Gli effetti speciali

E adesso l’effetto speciale: x * sin(100x). La funzione non oscilla più tra -1 e +1, ma ha un’ampiezza che, grazie alla moltiplicazione, aumenta con il valore di x.

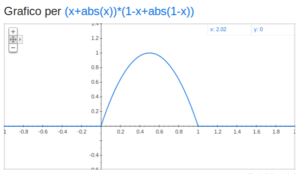
Giocando sull’effetto di moltiplicazione e divisione di funzioni, quali quelle trigonometriche, la radice quadrata (sqrt) e il valore assoluto (abs), si possono ottenere effetti decisamente carini.

Come esempio, si veda la figura che rappresenta una porzione di parabola.
Un aiuto a capire come è costruita può venire dall’esame delle sue due componenti, considerate come funzioni separate:
x + abs(x), 1-x+abs(1-x)

Ovvio che, all’annuncio di Google nel dicembre del 2011, si siano scatenati sul web i creatori di immagini. Mi feci coinvolgere anch’io, realizzando il disegno che ancora oggi campeggia sul mio profilo twitter:

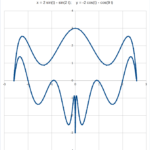
sqrt(1-x^2)(-.5+sin(400x)sin(4x))

Rappresenta due pesciolini in effusione. Il video riportato qui di seguito, che registrai all’epoca, visualizza la costruzione del disegno. La pagina della search di Google è datata (risale a fine 2011), ma il disegno funziona ancora.

Dei disegni memorabili di quell’epoca ne segnalo due, ben più complessi del mio:

1. il cuore nerd: sqrt(cos(x))*cos(300x)+sqrt(abs(x))-0.7)*(4-x*x)^0.01, sqrt(6-x^2), -sqrt(6-x^2) from -4.5 to 4.5 (visualizza su Google). Ebbe un discreto successo nel San Valentino 2012;
2. Batman: quattro funzioni intricate, che si combinano per visualizzare la sagoma di Batman (visualizza su Google).

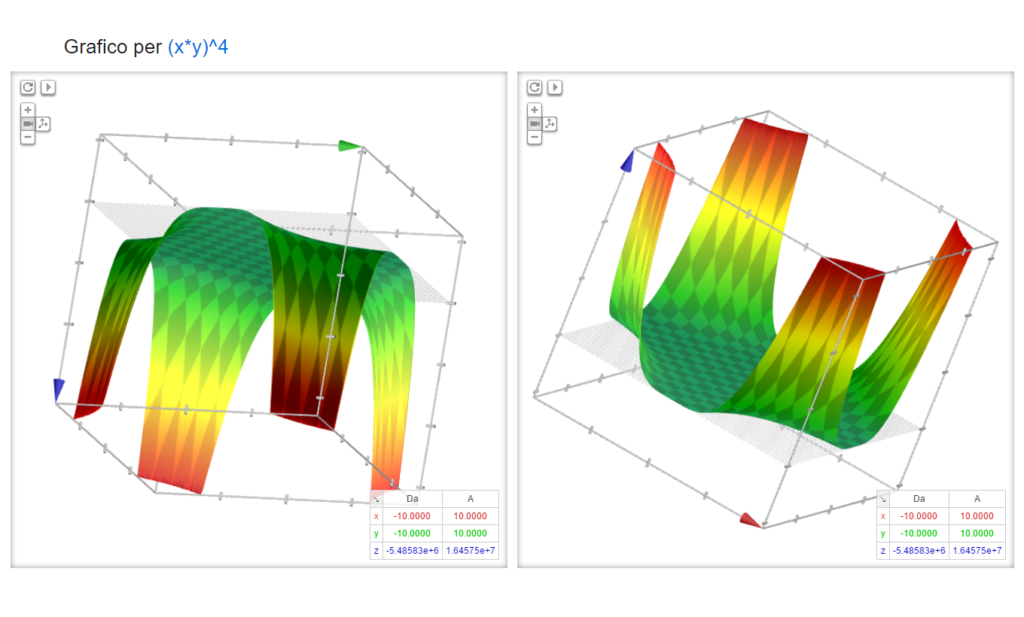
Nel marzo dell’anno successivo Google introdusse la possibilità di tracciare funzioni di due variabili, quindi figure 3D.
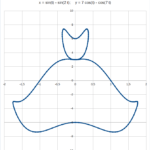
Nella foto di apertura del post ho riportato due viste di uno sgabello, di equazione (x * y)⁴. Resta da verificare l’effettiva comodità di una seduta del genere.

Disegnare con il pc utilizzando Excel 

Disegnare con il pc ed Excel è abbastanza semplice: data una funzione, si inseriscono in due colonne adiacenti i valori delle coordinate (x,y) dei punti che vogliamo tracciare, e poi si inserisce il grafico relativo. A rendere divertente il gioco è la scelta della funzione.

Un buon punto di partenza è il sito wolfram.com: una volta selezionata una curva, si gioca sui parametri per modificarne la forma, ottenendo dei risultati spesso sorprendenti.

Partiamo, ad esempio, dalla classica Cardioide, a cui si arriva cliccando sulla sezione Roulettes della pagina di wolfram.com. La Cardioide deve il nome alla sua forma, che ricorda un cuore. A battezzarla fu il matematico toscano Giovanni Francesco Salvemini, che per primo così la chiamò in un contributo alle Philosophical Transactions of the Royal Society nel 1741.

Dal punto di vista geometrico si definisce come:

il percorso di un punto scelto su una circonferenza che viene fatta rotolare senza scivolamenti intorno ad un’altra circonferenza di raggio uguale e mantenuta fissa.

La cardioide è una curva chiusa. Per tracciarne il grafico è preferibile partire dall’espressione in forma parametrica delle coordinate dei suoi punti:

x = 2 sin(t) – sin(2 t)
y = 2 cos(t) – cos(2 t)

Rispetto alla definizione classica, ho scambiato l’espressione di x ed y, in modo da raddrizzare la posizione del cuore.

Giocando con la cardioide

Su cosa si può giocare per creare variazioni della forma della Cardioide?
Le coordinate x,y sono ottenute combinando le funzioni seno e coseno del parametro t, con quelle di 2t. Viene naturale chiedersi cosa accade se si agisce sul peso degli addendi e sul moltiplicatore di t, e quindi tracciare il grafico di:

x = A sin(t) – sin(N t)
y = B cos(t) – cos(M t)

facendo variare i valori di A, B, M ed N.

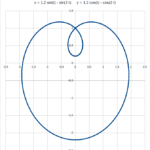
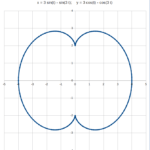
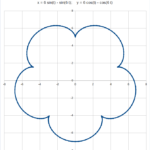
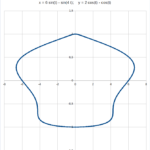
Esempio: se si porta il valore di A e B da 2 a 1.2, la punta del cuore si trasforma in un cappio. Portando da 2 a 3 il valore di A, B, M ed N si ottiene una forma simmetrica di due mezzi cuori uniti. Anche se la forma può ricordare qualcosa di molto meno poetico.

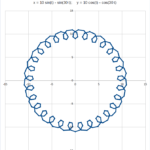
Di seguito una piccola raccolta di disegni. I valori utilizzati per i parametri sono riportati in alto in ciascun disegno.
Come si vede, alcune delle forme ottenute sono decisamente distanti dal cuore di partenza.
Per chi volesse cimentarsi, il programma excel è scaricabile da questo link.

E per finire, disegnare con il pc programmando in Basic

Uno dei linguaggi di programmazione più semplici è il Basic. Se da un lato ha mille difetti (strutturazione: niente; leggibilità: poca, oggetti: che roba è?), dall’altro richiede poca competenza informatica e porta rapidamente al risultato.

Utilizzo da anni un particolare dialetto Basic, l’UBASIC, progettato dal prof. Yuji Kida della università giapponese Rikkyo University, specializzato in mathematical computing.
Alla semplicità del Basic, l’UBASIC unisce una straordinaria ricchezza di funzioni (esempio: prmdiv(n) restituisce il più piccolo fattore primo di n), con un notevole risparmio di tempo nella scrittura dei programmi.

Utilizzo la versione 8.74 del 2005, stabilissima. L’installazione consiste semplicemente nello spacchettare il file zip di distribuzione. All’interno il file batch ubh.bat lancia l’ambiente basic e l’help contestuale.

Suggerimento: meglio stampare il file di help, che è in realtà il manuale di UBASIC.

Per utilizzare UBASIC una volta scaricato e spacchettato lo zip, occorre aprire una finestra DOS sul pc. Quindi su Windows basta eseguire il comando cmd, mentre su Ubuntu si può ricorrere all’emulatore DOSbox.
Quest’ultima combinazione (Xubuntu + DOSbox + UBASIC) è quella che uso da anni sul mio catorcetto casalingo, un AspireOne della Acer, risalente all’epoca dei netbook.

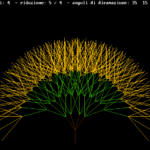
Un semplice programma UBASIC per disegnare un albero

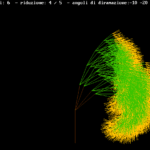
Un programma molto semplice da realizzare è la costruzione ricorsiva di un albero. Il programma si può scaricare da qui. Per aprirlo e modificarlo basta un programma notepad (il formato è un normale testo).
Il disegno parte dal tronco, poi si innestano dei rami, avendo fissato il fattore di riduzione della lunghezza del ramo rispetto al tronco e gli angoli di attacco dei rami sempre rispetto al tronco.

Per ottenere forme diverse di albero andranno modificate le righe 325, 345 e 355 del programma:

320 '---> numero di livelli dell'alberatura
325 nlmax=6
...
340 '---> riduzione di livello della lunghezza del ramo
345 k=4//5
350 '---> angoli di diramazione; si sommano all'angolo di attacco del ramo; se ="", il ramo non viene tracciato
355 a1=45: a2=20: a3=-15: a4=-30

Su ogni ramo si costruisce poi un secondo livello di ramificazione. Su questo un terzo e così via, fino a che si ha la pazienza di aspettare la conclusione del programma: con 4 rami si hanno 16 rami al secondo livello, 64 al terzo, 256 al quarto e così via.
Il programma che ho scritto è ricorsivo: una semplice routine traccia da 1 a 4 rami sulla base di un tronco; l’albero viene costruito considerando ogni ramo come tronco per il livello successivo. Più semplice da leggere il programma che racconta come funziona.

Qui di seguito qualche esempio che chiarisce quali risultati si possono ottenere. All’interno di ogni immagine, in alto, sono riportati i fattori di riduzione e gli angoli utilizzati.

Non resta che scegliere da dove cominciare, e provare: disegnare con il pc si rivelerà molto più semplice di quanto si possa immaginare. Buon divertimento!