Magic 19. E no, non si parla di covid

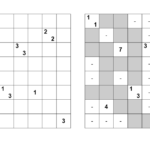
Magic 19 è il nome con cui la rivista web Plus.math.org ha pubblicato qualche anno fa un divertente puzzle, basato sulla disposizione di numeri interi su una griglia, in modo da soddisfare alcuni specifici requisiti.
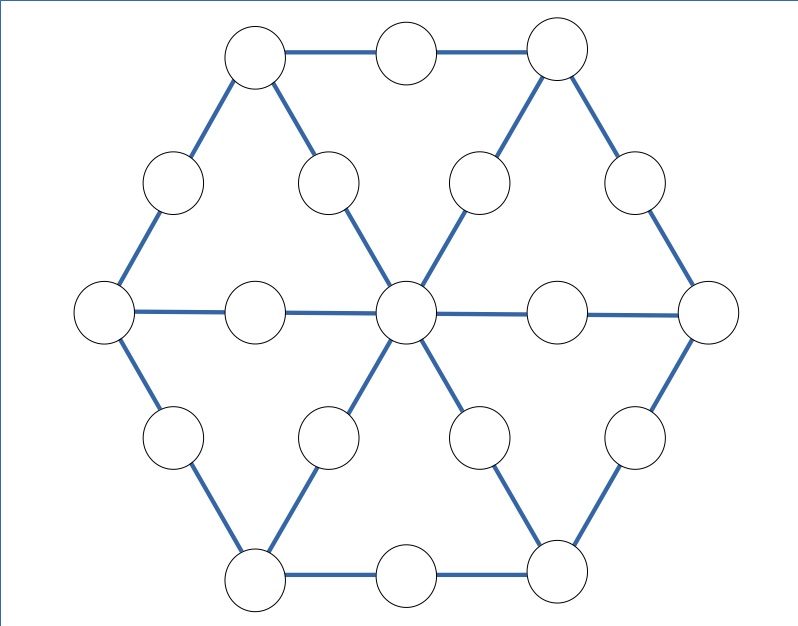
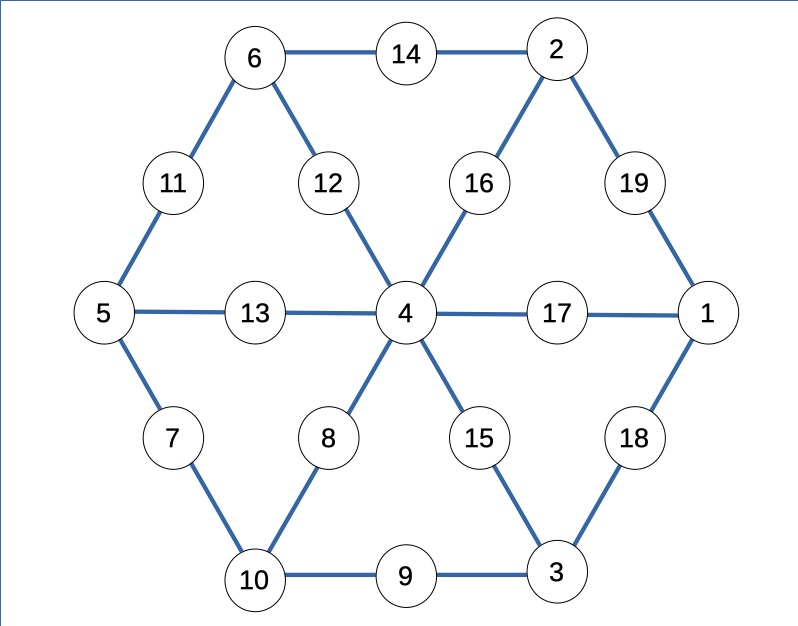
Le regole del Magic 19 sono molto semplici: occorre disporre gli interi da 1 a 19 in una griglia esagonale come quella mostrata qui sotto, in modo che tutte le triple di interi connesse da un segmento sommino 22.

Magic 19 può essere risolto con carta e penna (e ragionamento, ovviamente), oppure con l’aiuto di un programma, facendo ricorso sostanzialmente alla forza bruta. E, sorpresa, le soluzioni possibili sono 4 (una in più delle tre riportate da Plus.math.org).

Magic 19 e forza bruta

Un algoritmo di risoluzione basato sulla forza bruta consiste nell’esplorazione sistematica di tutte le possibili disposizioni o combinazioni, verificando per ciascuna se rappresenta o meno una soluzione del problema.
Nel caso di Magic 19, l’osservazione da cui partire è che, una volta inseriti gli interi nelle 6 caselle di vertice dell’esagono e nella casella centrale, il contenuto delle restanti 12 caselle è completamente determinato.

Il codice risolutore dovrebbe quindi assegnare alle 7 celle una combinazione di interi diversi tra loro, completare poi la griglia e verificare se è una soluzione o meno.
Si può stimare il tempo di esecuzione di un programma così strutturato, tenendo conto che occorrerà ciclare su 19⁷ = 893.871.739 differenti disposizioni. Tantissime!
Ma questo approccio ha anche un altro aspetto da considerare. Per come è concepito, l’algoritmo tirerà fuori come soluzioni tutte le possibili rotazioni e riflessioni speculari riconducibili a una soluzione intrinsecamente unica. A meno di filtrare a mano, post-esecuzione del codice, si dovrebbe istruire il codice stesso a non generare i duplicati, o a filtrarli una volta generati.
Entrambe le soluzioni richiedono del codice aggiuntivo, con una complicazione dell’algoritmo che preferirei evitare. Occorre trovare un’altra strada.

Qualche considerazione numerica

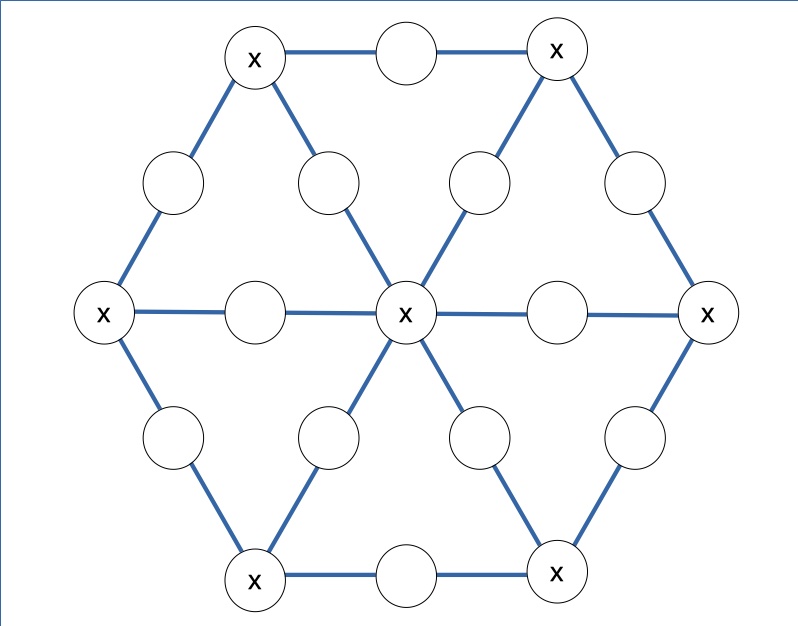
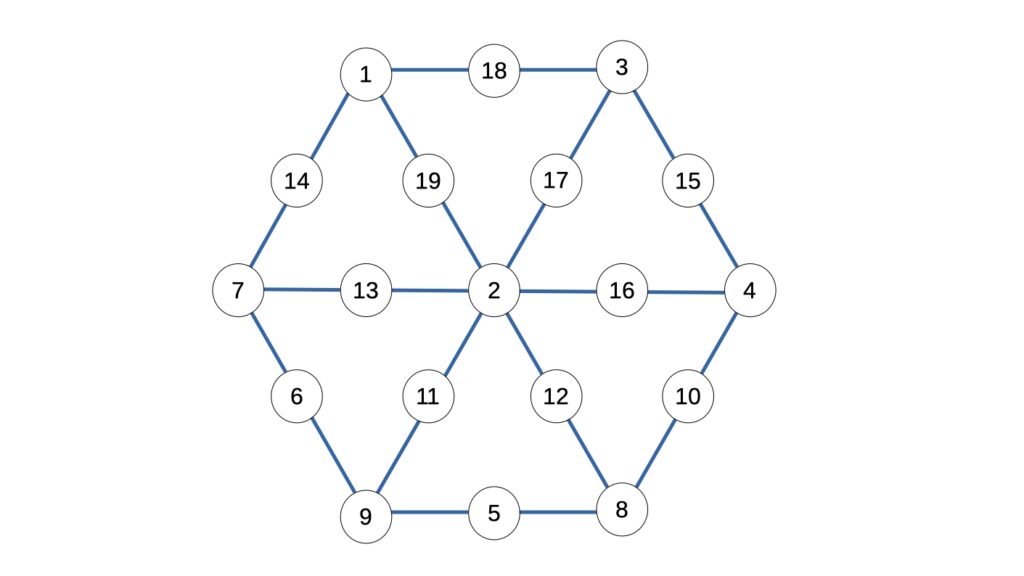
Osservando la griglia, si nota che le 19 caselle possono avere uno tra 4 ruoli distinti. Nella figura che segue, i 4 tipi di casella sono marcati con le lettere x, y, w, z.

In dettaglio:

la casella centrale, contrassegnata con x;
le 6 caselle interne, poste intorno al centro, marcate con y;
quelle poste ai vertici dell’esagono, ancora 6, identificate con w;
le altre 6 poste al centro dei lati dell’esagono, marcate con z.

Se con x, y, w e z indichiamo anche la somma del valore delle caselle, allora valgono le relazioni che seguono:

x + y + w + z = 1 + 2 + … + 19 = 190
6x + y + w = 6 * 22 = 132
2w + z = 6 * 22 = 132

Ora:

dalla 2 segue che y + w è pari (= 132 – 6x);
analogamente, dalla 3 segue che z è pari (= 132 – 2w);
applicando questo risultato alla 1, ne deriva che x + z è pari, quindi che x è pari.

Questo risultato già consente una buona potatura dell’albero delle possibilità. Ma si può fare ancora di meglio, elaborando le tre equazioni precedenti e inserendole in una tabellina excel.

Combinando la 2 e la 1:
- x + 132 – 6 x + z = 190
- z = 190 – 132 + 5x = 58 + 5x
Dalla 3:
- 2w = 132 – z = 132 – 58 – 5x = 74 – 5x
- w = 37 – 5x/2
Dalla 2:
- y = 132 – 6x – w = 132 – 6x – 37 + 5x/2 = 95 – 7x/2

A questo punto si possono impostare valori successivi pari per x e ricavare il valore corrispondente di y, w, z.

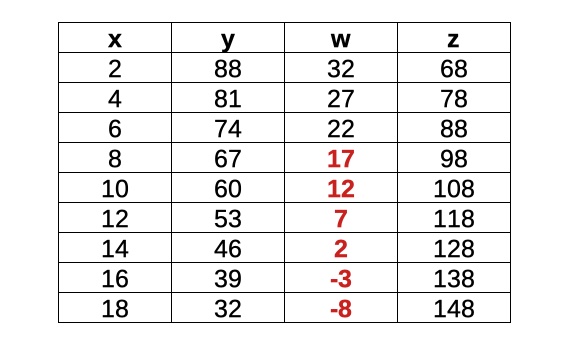I valori in rosso indicano che alla riga non può corrispondere una soluzione al problema, perché w non raggiunge il valore minimo possibile, pari a 1 + 2 + 3 + 4 + 5 + 6 = 21.
Rimangono quindi solo tre possibilità da esplorare per x: 2, 4 e 6.

Dove mettere il 18 e il 19?

Il 19 e il 18 sono decisamente ingombranti, dovendo sistemarli in terne di numeri che danno 22 come somma.
Per il 19 non c’è molto da scegliere, la terna che lo contiene può essere solo 1, 2, 19. Quindi il 19 va posto o in una casella y o in una casella z.

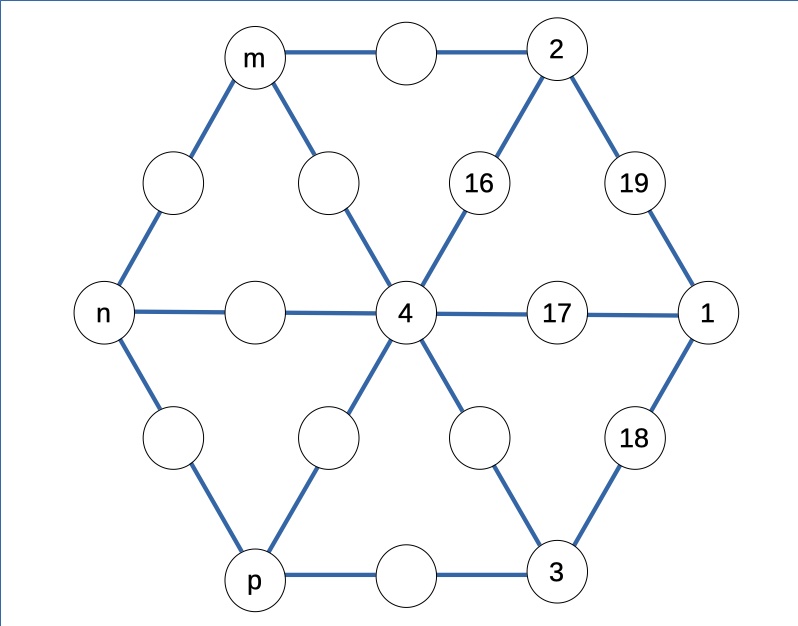
Se al centro c’è il 2, allora il 19 sarà su una casella y e 1 sul vertice corrispondente dell’esagono. A questo punto si sistemano immediatamente anche il 18 e il 3, e di conseguenza il 17.
Ci sono due importanti risultati! Primo: avendo fissato i valori di alcune caselle, oltre al centro, le soluzioni che eventualmente si troveranno per questa via sono essenzialmente uniche. Quindi è superato il problema del filtro. Secondo: rimangono solo 4 caselle di cui esplorare la combinazione di valori (marcate con m, n, p, q), nel campo ristretto da 4 a 16 inclusi.

Se, invece, al centro c’è il 4, allora 1, 19, 2 saranno necessariamente su un lato dell’esagono. Si sistemano immediatamente anche il 16 e il 17, quindi il 3 e il 18.
Rimane da esaminare la combinazione di valori delle 3 caselle marcate con m, n, p, nel campo di valori ristretto da 5 a 15 (inclusi).
Anche in questo caso le soluzioni trovate non includeranno rotazioni o riflessioni.

Un caso da escludere

Nella tabellina excel riportata in precedenza, rimane ancora da esaminare il caso con il 6 al centro della griglia.
In questo caso la terna 1, 19, 2 sarà su un lato dell’esagono, il 3 e il 18 si posizionano di conseguenza, come il 14 e il 15.

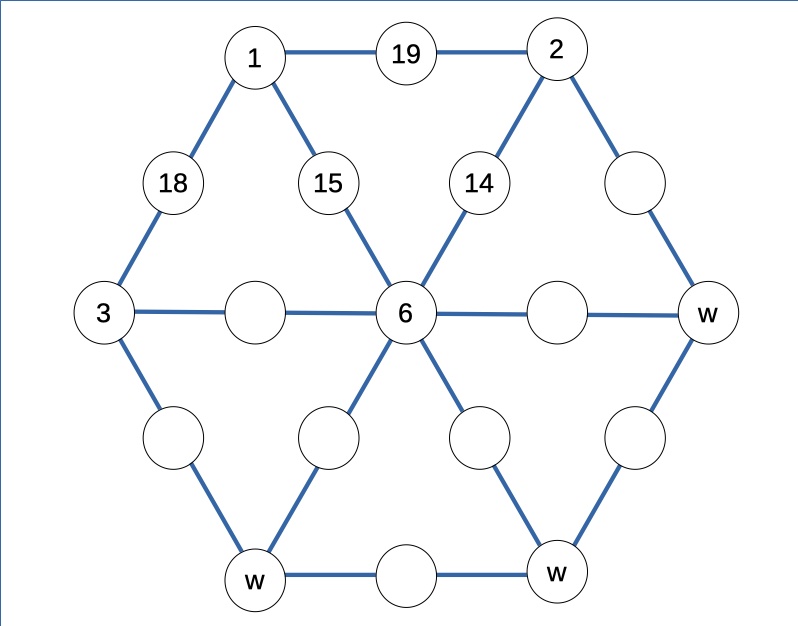Rimangono tre caselle w da riempire. Ricordando che, dalla tabella excel, la somma delle caselle w deve essere pari a 22, e che a tre è stato già assegnato un valore (1, 2 e 3), la somma delle restanti 3 deve essere 16. E 16 può essere raggiunto solo con i valori 4, 5 e 7.

Ora, in basso a sinistra non può esserci 4 (4 + 3 = 7, ma il 15 è già stato disposto sulla griglia). Non può esserci nemmeno 5 (5 + 3 = 4, ma il 14 è già sulla griglia). Quindi, al più, può esserci il 7 (e quindi si posiziona anche il 12 = 22 – 3 – 7).
Nella casella tutta a destra non può andarci il 4 (perché occorrerebbe inserire una seconda volta il 12, per completare 6 + 12 + 4 = 22).
Per lo stesso motivo, infine, il 4 non può andare nemmeno in basso a destra, perché, per completare il 22 con il centro, occorre ancora una volta il 12.

E ora fuori le soluzioni!

Poche righe di Python consentono di affrontare il caso con il 4 al centro.

print ("Caso di 4 al centro dello schema:")
for m in range(5,16):
    for n in range(5,16):
        for p in range(5,16):
            mask = list("|-------------------")
            mask[m] = "x"
            mask[20-m] = "x"
            mask[18-m] = "x"
            mask[p] = "x"
            mask[18-p] = "x"
            mask[19-p] = "x"
            mask[n] = "x"
            mask[18-n] = "x"
            if 22-n-m > 0:
                mask[22-n-m] = "x"
            if 22-n-p > 0:
                mask[22-n-p] = "x"
            if ''.join(mask[5:15]) == "xxxxxxxxxx":
                print ("m =", m, ",", "n =", n, ",","p =", p)

La logica del codice è abbastanza semplice:

si esplorano tutte le possibili combinazioni dei tre restanti vertici da trovare, con valori compresi tra 5 e 15 inclusi;
per ogni combinazione si completa la griglia;
infine si verifica se tutti i valori tra 5 e 15 inclusi sono stati inseriti nella griglia; se è così, si è trovato una soluzione.

Il programma dà come risultato:

Caso di 4 al centro dello schema:
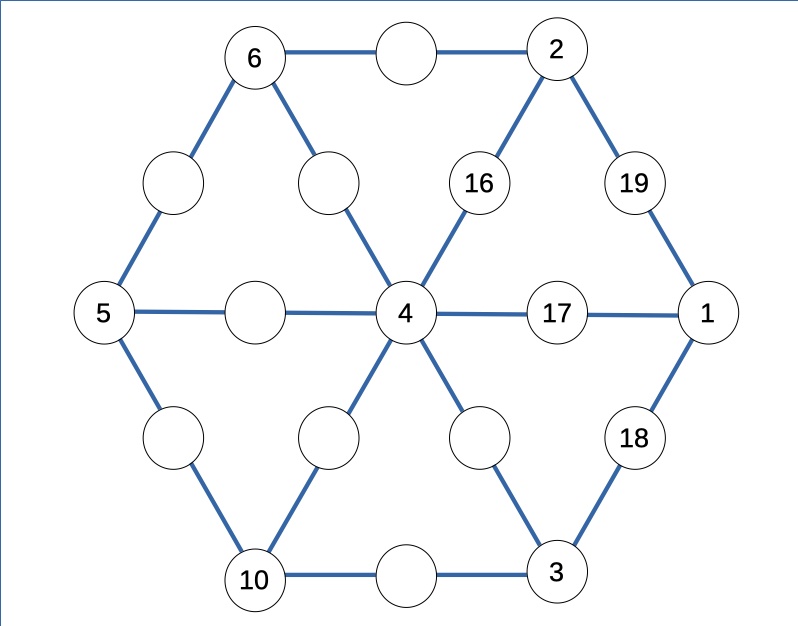
m = 6 , n = 5 , p = 10

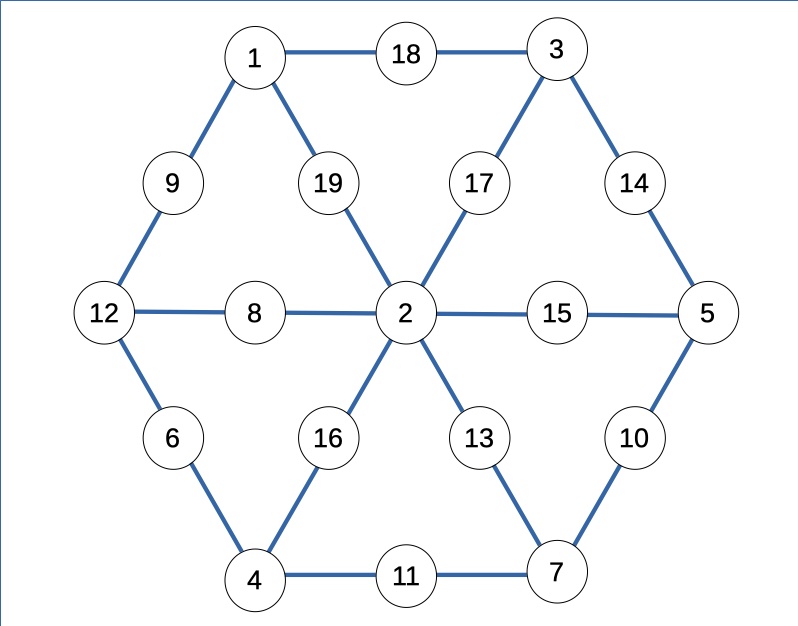
Cioè:

Completando la griglia, la soluzione è la seguente:

E, infine, il caso con il 2 al centro

Il codice per il caso con il 2 al centro della griglia è solo un po’ più complicato, dovendo analizzare le combinazioni di 4 vertici (uno in più del caso precedente).

print ("Caso di 2 al centro dello schema:")
for m in range(4,17):
    for n in range(4,17):
        for p in range(4,17):
            for q in range(4,17):
                mask = list("|-------------------")
                mask[m] = "x"
                mask[21-m] = "x"
                mask[20-m] = "x"
                mask[n] = "x"
                mask[20-n] = "x"
                mask[22-m-n] = "x"
                mask[p] = "x"
                mask[20-p] = "x"
                mask[22-n-p] = "x"
                mask[q] = "x"
                mask[19-q] = "x"
                mask[20-q] = "x"
                mask[22-p-q] = "x"
                if ''.join(mask[4:17]) == "xxxxxxxxxxxxx":
                    print ("m =", m, ",", "n =", n, ",","p =", p, ",","q =", q)

L’output del programma:

Caso di 2 al centro dello schema:
m = 7 , n = 9 , p = 8 , q = 4
m = 8 , n = 4 , p = 11 , q = 5
m = 12 , n = 4 , p = 7 , q = 5

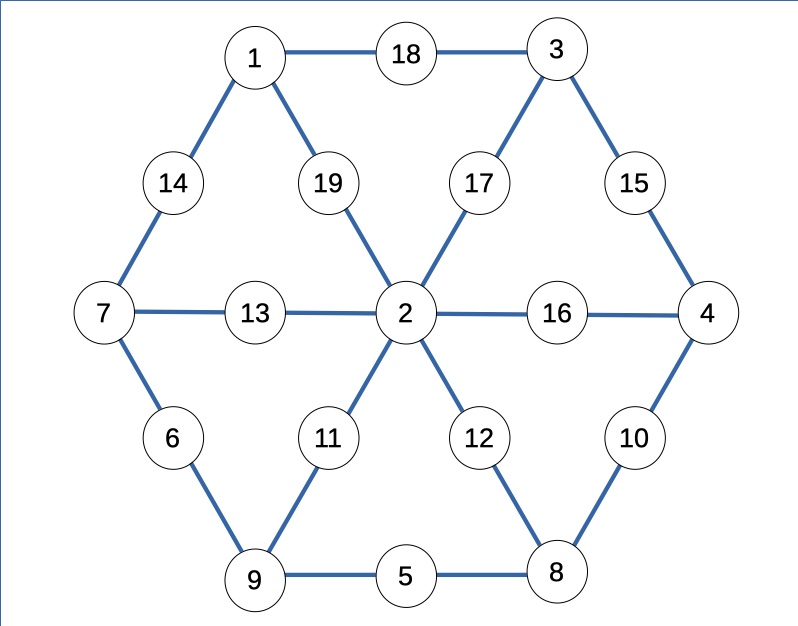
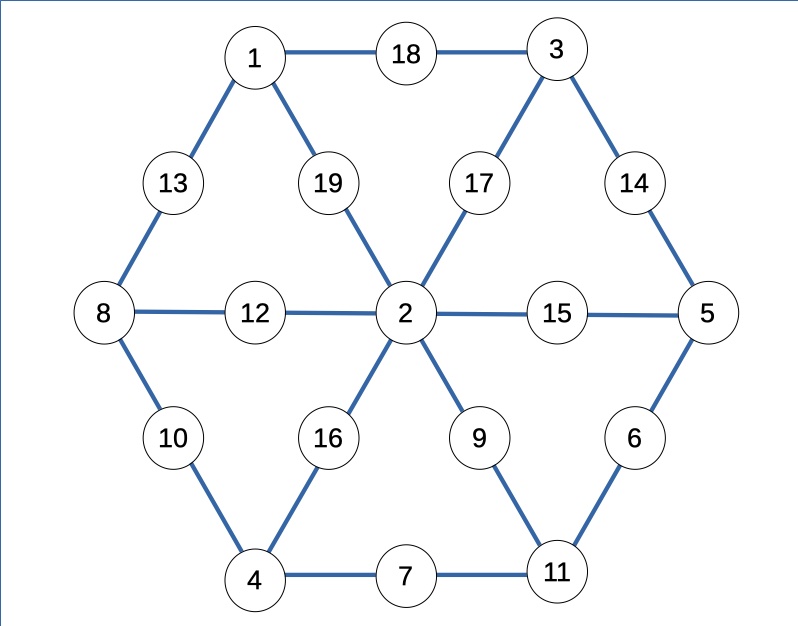
A ogni riga di output corrisponde una diversa soluzione al problema:

Una nota finale. Nella disposizione iniziale del 19, in entrambi i casi (2 o 4 al centro), era possibile disporre il numero in una qualunque delle 6 caselle della sua famiglia (y o w). Ho scelto la stessa posizione che il 19 occupa nelle soluzioni pubblicate da Plus.math.org, per consentire un agevole confronto tra i due articoli.