Negli U.S. ci sono oltre 150 math circles. Da dove arrivano i math circles ce lo racconta Wikipedia, mentre possiamo capire cosa sono oggi dal sito Mathcircles.org.
L’idea dei circoli matematici, diffusa nell’Europa dell’Est, principalmente in Bulgaria, dov’era nata agli inizi del ‘900, e in Russia, a partire dagli anni ’30, è stata importata negli U.S. negli anni ’90, grazie agli immigrati est-europei.
In estrema sintesi, è il lavoro che alcuni esperti di matematica dedicano su base volontaria a studenti liceali promettenti, introducendoli a questioni matematiche che altrimenti non sfiorerebbero. L’idea è quella di “incoraggiare il senso della scoperta e il piacere della matematica, attraverso la risoluzione di problemi e l’esplorazione interattiva. I problemi ideali […] possono essere affrontati con un minimo di background matematico, ma portano a concetti matematici profondi e possono essere collegati alla matematica avanzata“.
Organizzare un math circle comporta la risoluzione, su base volontaristica, di una serie di problemi: occorrono gli insegnanti giusti, serve lo spazio per gli incontri, vanno convinti genitori e studenti a preferire questa attività extra-curricolare ad altre.
Non ho notizia di iniziative del genere in Italia. Non sarebbe male, nel caso non ci fosse nulla del genere, che partissero anche da noi delle iniziative simili ai circoli matematici.
Maggiori dettagli sono disponibili sul sito Mathcircles.org; in particolare, la sezione Start a math circle, fornisce una guida su come creare un circolo, mentre nella sezione Math problems si può trovare una collezione di problemi proposti nei math circles.
La lingua degli ABBA, secondo i math circles
Uno dei problemi proposti riguarda una strana tribù che parla la lingua ABBA e la cui regina ama danzare (c’era da scommetterci).
Come funziona la lingua ABBA? Ecco le semplici regole grammaticali:
- ogni parola è una sequenza finita di A e B, inclusa la sequenza vuota; ad esempio AABABAA, BABA e BAAAA sono tutte parole del linguaggio ABBA;
- le sequenze AA, BB e BAB possono essere aggiunte o rimosse dalla fine di qualsiasi parola senza cambiarne il significato; ad esempio, BAABBB ha lo stesso significato di BAAB e BAA ha lo stesso significato di BAAAA;
- la sequenza ABA può essere cambiata in BAB, e viceversa, ovunque in una parola senza cambiarne il significato; ad esempio, BBBAB ha lo stesso significato di BBABA, che è sinonimo di BABAA.
Il problema pone tre questioni tutto sommato abbastanza semplici (ci ho penato solo una mattinata tra scarabocchi e retro-pensiero e un paio d’ore pomeridiane), ed apre poi a un tema più tecnico, che richiede approfondimenti. Partiamo dalla parte facile del problema. Si chiede di:
- trovare il più breve sinonimo della parola ABBA;
- trovare un paio di sinonimi per AB; qual è il più breve?
- creare un dizionario per la lingua ABBA, elencando il sinonimo più breve per ciascuna parola.
La chiave di volta del problema
Quando si affronta un problema di cui non si conosce a priori la strategia di soluzione, è bene armarsi di carta e penna e cominciare a giocare con le regole del problema. Muovendosi a caso si imboccano strade senza uscita, ovvio, ma qui e là si inciampa in qualche spunto di riflessione. E, soprattutto, si familiarizza con le regole del gioco.
Per cominciare, cosa possiamo dire del dizionario? Certamente avrà tre termini: A, B, e la sequenza vuota, che indichiamo con Ø. Per quanto riguarda le regole, si può intanto combinare la possibilità di cambiare BAB in ABA, con la possibilità di aggiungere o rimuovere BAB in fondo di parola. Evidentemente, quindi, anche ABA può essere aggiunta o rimossa in fondo di parola.
Le prime semplici osservazioni riguardano le lunghe sequenze di A o di B. Esempio:
AAAAAA (6 A) → AAAA (4 A) → AA → Ø, mentre:
AAAAAAA (7 A) → AAAAA (5 A) → AAA → A,
applicando la regola 2, nella facoltà di togliere coppie di lettere uguali dalla fine della parola. Quindi nessuna sequenza di lettere uguali si va ad aggiungere al dizionario.
Cosa succede se alla sequenza di A si aggiunge una B in fondo?
Si allunga per poi accorciare!
Partiamo da una sequenza breve, ad esempio da AB, ed esploriamo la strada di aggiungere qualcosa al fondo. Trasformiamo AB in ABAA.
Ora possiamo intervenire sulla sequenza iniziale ABA, il che aprirà a sua volta la possibilità di accorciare:
AB → ABAA → BABA → B.
Il risultato è notevole: nella sequenza AB in finale di parola, la A viene mangiata. Per simmetria, senza ripetere l’intero ragionamento, la sequenza finale BA si trasforma in A, questa volta è la B ad essere mangiata.
Quindi si può concludere che, data una qualunque sequenza di A e B, che contenga almeno due caratteri:
- se le ultime due lettere sono uguali (AA o BB), queste si possono eliminare e la sequenza si accorcia di due caratteri;
- se le ultime due lettere sono diverse (AB o BA), si può eliminare la penultima lettera, e la sequenza si accorcia di un carattere.
Ed eccoci alle risposte alle domande dei math circles
- trovare il più breve sinonimo della parola ABBA:
- ABBA → ABA → AA → Ø;
cosa che, devo dire, delude un po’, gli Abba mi sono sempre piaciuti; in realtà è la bionda, quella della prima A, Agnetha Fältskog, che mi è sempre piaciuta e lei, in quanto A, è nel dizionario!
- ABBA → ABA → AA → Ø;
- trovare un paio di sinonimi per AB; qual è il più breve?
- AB → B è certamente il più breve;
- BAA, ma anche BBB sono ulteriori sinonimi;
- creare un dizionario per la lingua ABBA, elencando il sinonimo più breve per ciascuna parola;
- se, come visto più su, una qualunque sequenza della lingua ABBA può essere accorciata di uno o due caratteri, a forza di accorciare possono succedere solo due cose:
- rimane un solo carattere, A o B;
- non rimane nulla, la sequenza si riduce alla stringa vuota Ø;
- quindi il dizionario ABBA rimane quello che già conoscevamo: A, B, Ø.
- se, come visto più su, una qualunque sequenza della lingua ABBA può essere accorciata di uno o due caratteri, a forza di accorciare possono succedere solo due cose:
Ora viene la parte difficile del problema
Ecco le ultime due domande del problema posto dai math circles:
- legate tre corde da 10 ft ad un bastone lungo 2,5 ft; formate una treccia con le tre corde, quindi fissate le estremità delle corde a un secondo bastone da 2,5 ft; sotto quali condizioni si può sciogliere la treccia, senza liberare le corde dal bastone inferiore?
- cosa ha a che fare questa domanda con la lingua ABBA?
Qui mi sono arenato.
Non ho ancora provato a formare la treccia, perché dovrei prima imparare come si fa, e poi sicuramente mi incasinerei con le tre corde da 10 ft ( = 3 metri!) ciascuna.
Ho però googlato per il termine “magic braid“, o treccia magica, e ho trovato alcuni tutorial su come ricavare un bracciale (o collare) intrecciato da un’unica striscia di cuoio. Il video che segue è un po’ lunghetto, ma è il più chiaro nei passaggi manuali:
Il problema posto dai math circles consiste nel trovare sotto quali condizioni si può disfare la treccia, cioè eseguire a rovescio i passaggi visti nel video.
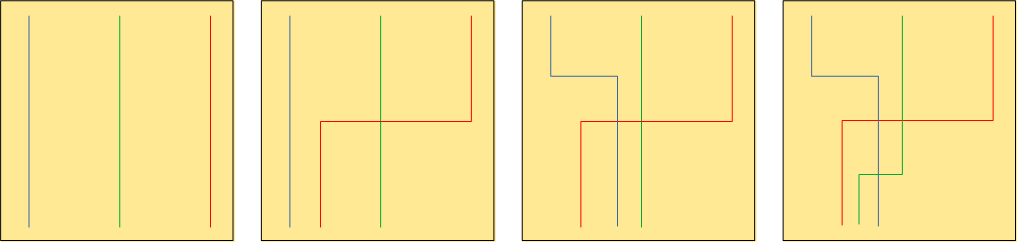
Al tempo 2’30” del video avviene il primo passaggio della treccia: striscia destra sul medio – striscia sinistra sul medio – striscia destra sul medio. Quello che avviene è che si scambiano di posizione le strisce laterali, mentre sotto, vicino al lembo inferiore, si formano gli intrecci simmetrici.
Seguiamo gli intrecci
La mossa successiva consiste nel far passare il lembo inferiore tra le due strisce a destra.
Poi, giro simmetrico: striscia sinistra sul medio – striscia destra sul medio – striscia sinistra sul medio – passaggio del lembo inferiore tra le due strisce a sinistra. By magic, al tempo 3’00” i due lembi sono per dritto, sullo stesso piano, e le tre strisce sono intrecciate.
Contiamo gli spostamenti della striscia inizialmente più a sinistra (blu), indicando con +1 lo spostamento verso destra e +1 lo spostamento in alto:
primo passaggio: (0,0) + (+1, +1) + (+1, -1) = (+2, 0);
secondo passaggio: (0,0) + (-1, +1) + (-1, -1) = (-2, 0).
Quindi la striscia blu, dopo i due passaggi, riprende esattamente la sua posizione sia in orizzontale che in verticale. Lo stesso avviene per le altre due strisce, quindi il groviglio che si è creato al di sotto può essere sbrogliato, ritornando in piano.
Detto ciò, mi rimane il mistero di cosa c’entri la treccia magica con il linguaggio degli ABBA. Un altro punto su cui lavorare, dopo il problema degli yogurt. Appena formano i math circles in zona, mi iscrivo. Ma me ne serve uno per la terza età!
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.