Sudoku, e si dia inizio all'estate

Sudoku ed estate al mare sono, per le mie abitudini, due (in)attività strettamente legate.
L’altro momento in cui mi ritrovo a riempire griglie di Sudoku è in treno, in occasione di lunghi viaggi. In entrambe le situazioni, mentre il corpo è in fase di stasi, la mente reclama di lavorare su qualcosa.

Il Sudoku è un gioco recente, arrivato in Italia nella primavera del 2005, pochi mesi dopo il suo sbarco in Europa, proveniente dal Giappone. Eppure la sue radici remote sono sorprendentemente occidentali. Svizzere, per la precisione.

Altra sorpresa, la natura del suo legame con la matematica. Sono in molti a classificarlo tra i giochi matematici, perché utilizza le cifre dall’1 al 9, e a ritenere che stimoli il pensiero laterale.
Niente di tutto ciò, il Sudoku non richiede nessun calcolo, si potrebbe giocare con delle lettere al posto delle cifre. E niente pensiero laterale, il gioco si risolve con un buon colpo d’occhio e applicando una rigorosa catena di passaggi logici.

Preparare griglie di Sudoku da risolvere è invece un’interessante sfida algoritmica.

La storia del Sudoku: le origini lontane

I quadrati più o meno magici sono una passione per la mente umana.
Il primo che si ricordi è il latercolo pompeiano. I più antichi sono stati ritrovati a Pompei, nella casa di Publio Paquio Pròculo (mi raccomando l’accento) e nella Palestra grande. Ce n’è poi a bizzeffe in strutture ecclesiastiche dell’alto medioevo, sia italiane che europee.

L’iscrizione reca una frase palindroma, divisa in cinque parole di cinque lettere:

SATOR AREPO TENET OPERA ROTAS

In molti hanno provato a dare un senso compiuto alla frase, ma non c’è concordanza. SATOR è il seminatore, ROTAS sono le ruote, TENET sta per mantiene, conserva e simili. OPERA starebbe per con cura. AREPO è un po’ un mistero, non essendo una parola strettamente latina.

Potrebbe stare per aratro, ma ci sono tante letture diverse per questa frase enigmatica. I due TENET incrociati a formare una croce, ad esempio, alimentano il filone a sfondo religioso.
Personale opinione: chi l’ha ideato ha forzato le parole per creare il palindromo, il resto è opera di un sano complottismo ante litteram.

La storia del Sudoku: quadrati magici & co

Saltiamo alcuni secoli, fino al 1514, ed ecco un primo utilizzo di numeri con Melacholia I, incisione di Albrecht Dürer. In un particolare dell’incisione si nota il quadrato con i numeri da 1 a 16 disposti a formare somme uguali nelle righe, nelle colonne e nelle diagonali.
Al centro dell’ultima riga si legge la data dell’incisione, 1514.

E la Svizzera? Ancora un paio di secoli, fino al ‘700, e troviamo il matematico svizzero Eulero che, tra i mille interessi e lavori che porterà a compimento, si occupa anche di quadrati speciali: i quadrati latini e i quadrati greco-latini.

Il quadrato latino è il progenitore del nostro Sudoku: si tratta di distribuire n simboli in un quadrato n x n, facendo sì che nessun simbolo si ripeta in alcuna riga o colonna.

Dal quadrato greco-latino, incrocio di due quadrati latini, verrà fuori invece il problema dei 36 ufficiali:

è possibile disporre su una piazza quadrata 36 ufficiali, provenienti a sei a sei da sei diversi reggimenti ed aventi, ciascuno di essi, sei gradi militari differenti, in 6 righe e 6 colonne da 6 ufficiali ciascuna, in modo che in ogni riga e in ogni colonna ci sia un ufficiale di ogni reggimento e di ogni grado?

Eulero ipotizzò l’impossibilità di soluzione, che sarà però dimostrata solo nel 1901 da Gaston Tarry. C’è invece una soluzione per il caso generale di N²ufficiali, con N diverso da 6.

Il Sudoku comincia a prendere forma

Sebbene Eulero avesse lavorato su quadrati latini 9×9, il suo intento era stato quello di scoprirne le proprietà logico-matematiche.
Perché prenda forma il gioco occorre attendere ancora un secolo, e passare a fine ‘800.

È il giornale francese Le Siècle a pubblicare intorno al 1892 un gioco per i propri lettori: quadrato 9×9, diviso in blocchi 3×3, da completare però con i numeri da 1 a 81.
Le regole: ciascuna riga e colonna, le due diagonali principali e ciascun blocco devono dare somma 369.
Negli anni successivi sui giornali rivali cominciano a girare varianti del gioco, incluso qualcosa di molto simile al Sudoku. L’arrivo della prima guerra mondiale cancella però tutto, e occorre aspettare ancora una sessantina d’anni.

Nel 1970, infatti, l’editore americano Dell Publisher propone ai suoi lettori il Number Place. È praticamente il Sudoku, mancano solo alcuni piccoli dettagli.
Ad aggiungerli ci pensa una decina di anni dopo l’editore giapponese Nikoli. Il suo Suji Wa Dokushin Ni Kagiru (la cifra deve rimanere single), aggiunge la simmetria dello schema (lo schema iniziale di un Sudoku che si rispetti deve essere simmetrico nella rotazione di 180°) e un limite alla quantità di numeri noti iniziali (non più di 32). Siamo nel 1984.

Cosa rimane da mettere a punto? Beh, il nome. Con quello lunghissimo iniziale non ci siamo. Sarà Maki Kaji, presidente della Nikoli, ad accorciarlo quasi subito in Su Doku.

Il ritorno in occidente

Nel 1997, Wayne Gould, giudice neozelandese in pensione, è in vacanza a Tokio. Gli piace leggere, ma quello che vede esposto nelle librerie di Tokio è decisamente ostico. Fanno eccezione le riviste della Nikoli, piene di griglie numeriche incomplete.
Si fa spiegare come funziona il gioco, ma sarà solo al ritorno a casa in Nuova Zelanda, qualche mese dopo, che prova a giocarci. Rimane intrappolato in poche ore.

Intuita la viralità del gioco, Gould si chiede quanto sia difficile programmare un pc per generare dei Sudoku. Non senza sforzo, dopo alcuni anni, nasce il suo generatore di schemi di Sudoku, che introduce l’ultimo pezzetto che mancava: la garanzia dell’unicità della soluzione.

Il suo programma, chiamato Pappocom Sudoku, dà anche vita a una piccola società di sviluppo software e al sito sudoku.com, dove ancora oggi è possibile giocare interattivamente.
Per dare un’occhiata a come era il sito agli inizi, basta chiedere ad archive.org, la memoria storica del web. Qui si può vedere la pagina www.sudoku.com nel marzo del 2001, la più vecchia testimonianza conservata (passando il mouse sulla griglia si visualizza la soluzione del puzzle).

Il sudoku sbarca in Europa

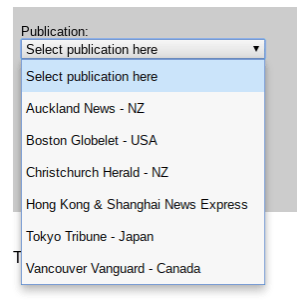Navigando nel fermo immagine del sito si trova anche la lista delle riviste che nel 2001 pubblicavano le griglie generate dalla Pappocom.
C’è ovviamente la Nuova Zelanda, poi Giappone, Cina, USA e Canada. Manca ancora l’Europa, che si aggiungerà a fine 2004, quando Gould propone il gioco al londinese Times, aprendo così il fronte occidentale:

I was on my way to Hong Kong via London. I turned up unannounced at the Times, like an old-fashioned travelling salesman, and got my foot in the door. They published the puzzle the following month and it took off.

Era l’ottobre del 2004. Il Sudoku sbarcherà sul Corriere delle Sera, e quindi in Italia, a giugno del 2005. L’anno dopo Gould è tra i World’s Most Influential People del Time magazine.

Una digressione: archive.com, come eravamo

Il sito archive.org, è gestito da una società no profit statunitense, e conserva fermi immagine di siti web presi via via nel tempo e conservati per ricordare come eravamo.
Curiosi di vedere come era agli inizi, che so, il sito di Repubblica.it? Si accede ad archive.org, si digita l’url del sito cercato nell’apposito riquadro in alto, e dopo qualche secondo si visualizza la time line degli anni di cui sono presenti dei fermi immagine. Se ne seleziona uno, quindi dal calendario mostrato appena sotto la timeline si sceglie uno dei fermi immagine disponibili.
Ecco la prima pagina di Repubblica.it il 14 febbraio del 2002.

Un breve riepilogo delle regole del Sudoku

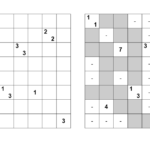
Il Sudoku si gioca su una griglia di celle 9×9, divisa in 9 blocchi di 3×3 celle, da riempire completamente di numeri dall’1 al 9.
Alcune celle già popolate all’inizio del gioco sono i dati. La disposizione dei dati rispetta, in genere, una simmetria rotazionale di 180°. Vale a dire che, capovolgendo verticalmente, e poi orizzontalmente la griglia, si ottiene una disposizione di celle piene uguale a quella di partenza.
In base ai dati va trovata l’unica soluzione possibile, rispettando la regola di inserire nelle 9 celle di ogni riga, di ogni colonna e di ogni blocco tutte le cifre dall’1 al 9, senza ripetere due volte la stessa cifra.

Come si trova la soluzione?

A partire dai dati, si riempiono progressivamente le celle analizzando se, in base alle regole del gioco:

in una cella è possibile un solo valore (esempio: se in una cella c’è un 2, allora tutte le altre celle nella stessa riga, colonna e blocco avranno un valore diverso da 2; tracciando una riga ideale di esclusione su ogni riga e colonna interessata, si può arrivare a determinare la posizione certa del 2 in un determinato blocco);
in una coppia di celle della stessa riga o colonna sono possibili solo due valori; anche se non si può determinare subito la loro posizione, quei due valori possono essere esclusi dal resto della riga o colonna;
stesso ragionamento del punto precedente, ma applicato a una tripletta di celle;
se in un blocco tre celle adiacenti sono occupate, non c’è posto per altre cifre (sembra ovvio, ma torna utile).

Su queste regole base si possono costruire catene di passaggi logici complessi a piacere, ricorrendo anche alla forza bruta: se in una cella sono possibili più valori, li provo uno alla volta fino ad escludere tutti, tranne uno, per raggiunta contraddizione.

Come si vede, c’è complessità, ci vuole colpo d’occhio, ma niente pensiero laterale.

Preparare un sudoku: i passi dell’algoritmo

Un ottimi articolo di livello accademico su algoritmi per la preparazione di sudoku si trova qui.

L’algoritmo si può scomporre in tre parti:

generare una griglia completa (la soluzione);
individuare, in base al livello di difficoltà desiderato, le celle da rendere note in partenza (da notare che, perché la soluzione derivata sia unica, occorre che ci sia un numero sufficiente di celle note);
risolvere la griglia proposta.

Quante sono le griglie complete possibili?

Un risultato che risale al 2003, successivamente confermato nel 2005, riporta il numero di 6.670.903.752.021.072.936.960 (circa 6,67×10²¹).
In realtà molte sono equivalenti tra loro. Basti pensare che, data una griglia, se ne ottiene un’altra valida semplicemente:

ruotandola di 90°, 180°, 270°;
ribaltandola in orizzontale o in verticale;
scambiando tra loro due righe o due colonne che interessino un solo gruppo orizzontale o verticale di blocchi;
scambiando tra loro due gruppi orizzontali o verticali di blocchi;
mescolando i simboli dal’1 al 9.

Le griglie primitive, tutte non equivalenti tra loro, tenendo conto dei primi tre criteri appena riportati, sono solo 5.472.730.538.

Partiamo dal fondo

Come si risolve una griglia proposta?

Il software può essere programmato per avere il colpo d’occhio necessario, ma possiede anche una capacità che manca all’uomo, la forza bruta computazionale.
Data la griglia incompleta di partenza, si possono quindi elencare tutte le griglie complete possibili, semplicemente provando, una cella alla volta, tutti i valori che in quel momento sono possibili per la cella stessa. In modo ricorsivo vengono quindi esplorate tutte le strade percorribili a partire dalla griglia incompleta di partenza.
Il procedimento annota via via le griglie complete raggiunte, mentre dimentica tutti i vicoli ciechi in cui finisce, quando in una cella non è possibile inserire nessun numero.

Questo passo dell’algoritmo torna utile per tre scopi:

quello ovvio del trovare la soluzione della griglia incompleta di partenza;
per verificare che una griglia incompleta abbia una sola soluzione, quindi sia un gioco valido;
per generare a caso una griglia completa di partenza.

Risaliamo la corrente

Secondo step: generare la griglia incompleta.
Occorre selezionare i dati, cioè le celle da rendere note all’inizio, in modo da raggiungere una soluzione unica, con il livello voluto di difficoltà.

Prima domanda: quante celle vanno popolate, come minimo? Nel 2012 è stato dimostrato, con l’aiuto del software, che sono necessarie almeno 17 celle.

Seconda domanda: come varia il livello di difficoltà con il numero di dati?
La risposta è articolata. Innanzitutto, in genere la difficoltà diminuisce al crescere del numero di celle note. Questa non è però una regola valida sempre. Basti pensare alle volte che ci si è bloccati dopo aver riempito alcune celle di uno schema: lo schema ha ora più dati, ma non è meno difficile di quello di partenza.

È certamente importante, invece, la distribuzione delle celle note, in particolare il numero di celle in ogni singola riga, colonna, blocco. Meglio sono distribuiti i dati, meno difficile sarà trovare la soluzione.

Conta poi il numero di indizi presenti nella griglia: quanti candidati singoli, coppie, triplette sono presenti inzialmente.

Tutti questi elementi possono essere valutati dal software, per assegnare un tasso di difficoltà a uno schema iniziale. Oppure possono essere selezionati a caso dal programma, in modo da raggiungere un livello di difficoltà prestabilito.

Ultimo step, anzi il primo: generare la griglia di partenza

Ed eccoci finalmente, al primo passo dell’algoritmo, la generazione della soluzione.

Un modo semplice per procedere è questo:

generiamo a caso una griglia incompleta iniziale; non importa che abbia una soluzione unica, anzi è meglio che ci sia da scegliere;
determiniamo, con il metodo ricorsivo, una qualunque possibile griglia completa di partenza;
se non si trova nessuna griglia possibile, si torna al passo 1, cambiando la disposizione iniziale.

Da quante celle note partire?
Occorre considerare che l’algoritmo si può completare in uno o più passi, a seconda della probabilità di successo del passo 2. Quindi c’è da bilanciare la probabilità di azzeccare il passo 2 (meno celle = maggiore probabilità), con il tempo necessario a trovare una soluzione (meno celle = più tempo per completare ogni singolo passo del metodo ricorsivo).
Un buon valore di partenza è di 11 celle (cfr. articolo).

Ma, un metodo più semplice?

Una strada più semplice per generare griglie di Sudoku è utilizzata in qualche macro excel che si trova sul web. L’algoritmo ha un approccio decisamente pragmatico, anche se offre risultati è un po’ limitati.

Il ragionamento è semplice.
Parto da una griglia incompleta nota, di difficoltà nota. La posso copiare da una rivista, per esempio.
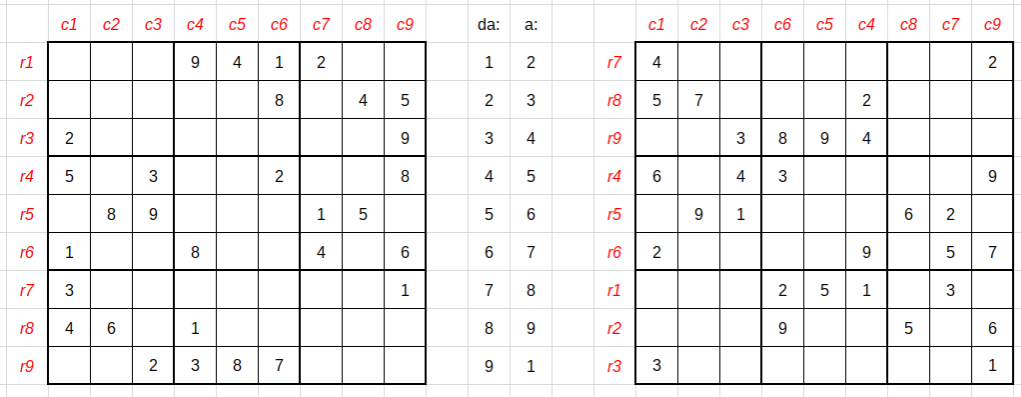
Alla griglia incompleta (e quindi anche a quella completa) posso applicare i passi invarianti elencati qualche paragrafo più su:

ruotarla di 90°, 180°, 270°;
ribaltarla in orizzontale o in verticale;
scambiare tra loro due righe o due colonne che interessino un solo gruppo orizzontale o verticale di blocchi, oppure…
scambiare tra loro due gruppi orizzontali o verticali di blocchi;
mescolare i simboli dal’1 al 9.

Quelle che si ottengono sono griglie visivamente diverse da quelle iniziali, ma sostanzialmente equivalenti, corrette e con un livello di difficoltà simile.

Basterà quindi avere una dozzina di griglie incomplete di partenza per ognuno dei livelli di difficoltà (semplice, medio, difficile), tra cui scegliere a caso il punto di partenza. E poi applicare un certo numero di volte i mescolamenti elencati.

Come premesso, i risultati sono relativamente limitati, ma il programma è molto più semplice da scrivere e da debuggare, ed è anche più veloce da eseguire.

Complicato?
Devo confessare che sì, non mi sarei aspettato che dietro la creazione di uno schema del Sudoku ci fosse questa miniera di spunti algoritmici. Mi toccherà guardare con maggior rispetto gli schemi che riempirò quest’estate, al riparo dell’ombrellone.