Poche settimane fa, un articolo della rubrica Science del New York Times suggeriva come risolvere un classico puzzle geometrico.
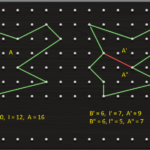
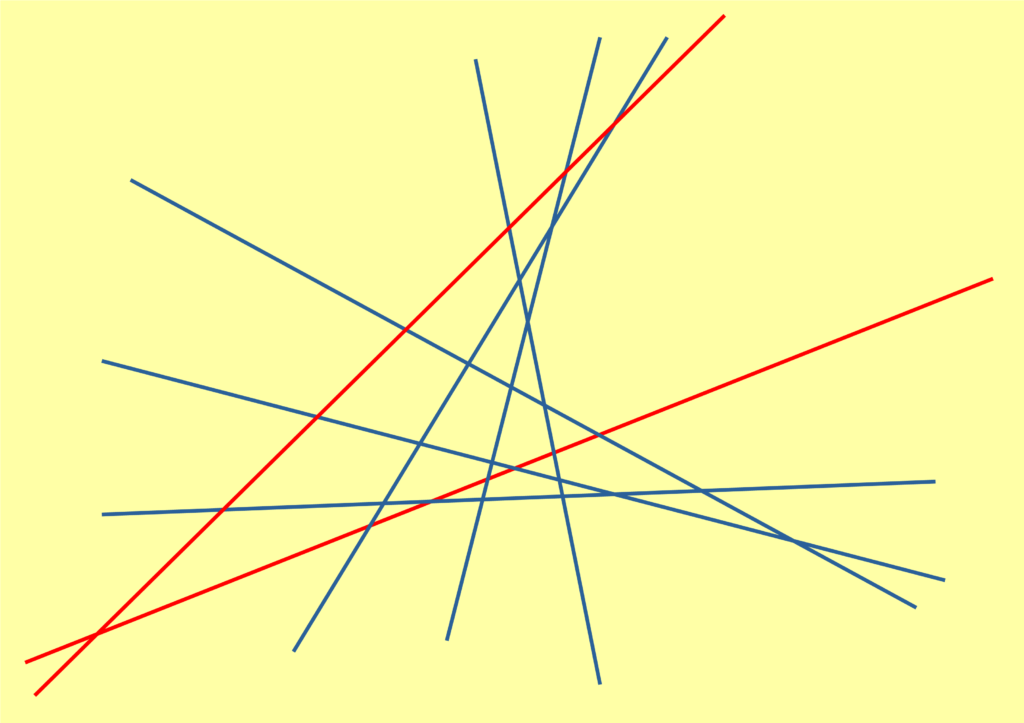
Si immagini di tracciare su un foglio N segmenti di rette a due a due non parallele e con non più di due rette passanti per uno stesso punto. L’immagine di apertura del post mostra il caso con 8 segmenti di retta; per facilitare il conteggio, due hanno un colore diverso dalle altre 6. Quanti triangoli vengono individuati dalle N rette?
Cominciamo con un caso semplice
Gli occhi si incrociano, nel cercare di individuare tutti i possibili triangoli, senza saltarne nessuno ed evitando di contarne più volte qualcuno. Evidentemente la via diretta non è una soluzione adeguata.
Proviamo allora ad affrontare un caso più semplice, cercando di trovare una linea di ragionamento generalizzabile a qualunque numero di rette.
Il caso di tre rette è evidentemente banale, perché viene individuato un solo triangolo. Partiamo allora con 4 rette.
Per semplificare, le rette sono state numerate da 1 a 4.
Un triangolo è certamente individuato dalle rette 1, 2 e 3. Ma cosa hanno di particolare queste rette?
In realtà si potrebbe individuare la prima retta in quattro possibili modi: 1, 2, 3 oppure 4. Se scegliamo la 1, allora la seconda retta può essere individuata in tre possibili modi: 2, 3 oppure 4. E, se scegliamo la 2, allora la terza retta potrà essere a sua volta scelta tra la 3 e la 4.
Quindi si hanno 4 possibili modi per scegliere la prima retta, a seguire 3 possibili modi per selezionare la seconda retta e, infine, 2 possibili modi per selezionare la terza retta. In tutto si avranno: 4 × 3 × 2 = 24 possibili scelte.
I triangoli sono però certamente meno, dov’è l’inghippo?
Nel ragionamento fatto ci sono triangoli contati più volte. Se indico con (1,2,3) il triangolo individuato dalle rette 1, 2 e 3, allora certamente ho contato anche (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1), tutti modi diversi di indicare sempre lo stesso triangolo. In totale, quindi, ogni triangolo è stato contato 6 volte, di conseguenza il numero corretto di triangoli è 24 ⁄ 6 = 4.
Una semplice verifica visiva ci dice che è così.
Aggiungiamo una retta
Inseriamo nel disegno una quinta retta, colorata in rosso per semplificare il conteggio dei nuovi triangoli.
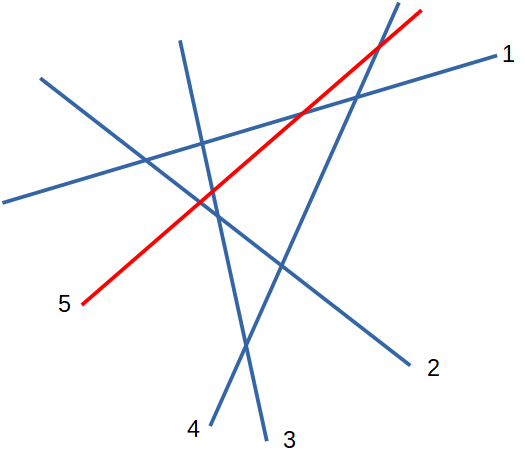Quanti triangoli sono stati aggiunti con l’inserimento della quinta retta?
Vediamo: (5,1,2), (5,1,3), (5,1,4), (5,2,3), (5,2,4), (5,3,4). In tutto 6, quindi siamo a 10 triangoli in totale.
Possiamo però ragionare come nel caso precedente, ottenendo 5 × 4 × 3 = 60 triangoli in base alle possibili scelte per ciascuno dei tre lati e poi, anche in questo caso, dividendo per i 6 modi diversi per annotare lo stesso triangolo: 60 ⁄ 6 = 10. Torna il nostro primo calcolo, con il vantaggio, però, di cominciare a intravedere un embrione di formula. Siamo passati, infatti, da:
4 × 3 × 2 ⁄ 6 = 4, a
5 × 4 × 3 ⁄ 6 = 10
In entrambi i casi la prima parte del calcolo è il prodotto degli ultimi tre termini del fattoriale del numero N di rette. Questo termine si può generalizzare in:
N! ⁄ (N-3)!
Formula che elimina dal prodotto di N! i termini di (N-3)!, lasciando quindi al loro posto i tre più pesanti: N, (N-1), (N-2).
La formula generale per il numero di triangoli individuati da N rette diventerebbe allora:
N! ⁄ ((N-3)! × 3!)
Verifichiamo!
Nel caso di 6 rette dovremmo trovarci:
6! ⁄ ((6-3)! × 3!) = 720 ⁄ (6 × 6) = 20 triangoli.
Ragioniamo sulla figura:
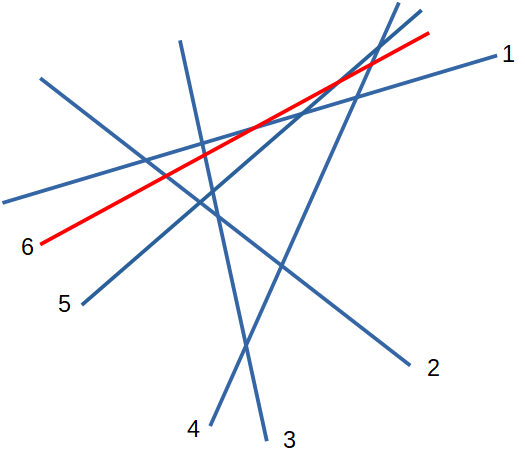Anche in questo caso si può verificare che il disegno include tutti i 5 i punti in cui la nuova retta incrocia le 5 precedenti.
Quanti triangoli sono stati aggiunti? Con la solita notazione, abbiamo:
(6,1,2), (6,1,3), (6,1,4), (6,1,5), (6,2,3), (6,2,4), (6,2,5), (6,3,4), (6,3,5), (6,4,5), vale a dire 10 nuovi triangoli. Aggiunti ai 10 precedenti, portano il totale a 20. Torna!
Quanti triangoli ci sono allora nell’immagine di apertura? La formula ci dice che sono:
8! ⁄ (( 8-3)! × 3!) = 40.320 ⁄ (120 × 6) = 56
Il problema a questo punto diventa verificare visivamente la soluzione. È un’operazione sicuramente al di sopra delle mie capacità operative. Peraltro, nella figura mi sono limitato a tracciare 8 rette solo perché non sono riuscito ad aggiungere la nona, realizzando tutti gli incroci e lasciando triangoli che fossero chiaramente visibili!
La formula ottenuta è in realtà ben nota nell’analisi combinatoria ed è quella che fornisce il numero di modi distinti di scegliere M diversi oggetti tra N disponibili, indipendentemente dalla disposizione degli oggetti scelti:
N! ⁄ ((N-M)! × M!)
Mi chiamo Pasquale Petrosino, radici campane, da alcuni anni sulle rive del lago di Lecco, dopo aver lungamente vissuto a Ivrea.
Ho attraversato 40 anni di tecnologia informatica, da quando progettavo hardware maneggiando i primi microprocessori, la memoria si misurava in kByte, e Ethernet era una novità fresca fresca, fino alla comparsa ed esplosione di Internet.
Tre passioni: la Tecnologia, la Matematica per diletto e le mie tre donne: la piccola Luna, Orsella e Valentina.
Potete contattarmi scrivendo a: p.petrosino@inchiostrovirtuale.it
Articoli correlati:
