L’eleganza del teorema di Pick

Il teorema di Pick fornisce una formula semplice ed elegante per il calcolo dell’area di poligoni reticolari, vale a dire poligoni costruiti su un reticolo regolare di punti.
La definizione può risultare astrusa ma, spulciando nei ricordi, forse riemergeranno la tavoletta di plastica forata e i chiodini della Quercetti. Basta inserire ordinatamente un po’ di chiodini e procurarsi qualche elastico per realizzare dei poligoni reticolari.

Naturalmente una geoboard, come la chiamano gli anglosassoni, si può realizzare anche con un po’ di compensato e dei chiodini veri.
Per i pigri esistono invece le versioni web. Segnalo la geoboard del mathlearningcenter.org, con cui ho preparato i disegni di questo post.

Tornando al teorema di Pick, più che l’utilità colpisce l’eleganza dell’enunciato e delle dimostrazioni che sono state formulate nel tempo.

---

Chi era Pick

Un’ottima biografia di Georg Alexander Pick si trova sul sito della università scozzese di St Andrews.
Nato a Vienna nell’agosto del 1859, fu matematico e accademico di professione, buon musicista per passione. Oggi è ricordato per tre motivi:

• il suo teorema sull’area dei poligoni costruiti su reticoli regolari di punti (1899);
• l’essere stato il maggior sponsor di Einstein nella commissione che attribuì al grande scienziato una cattedra all’università tedesca di Praga (1910);
• la sua tragica fine nel campo di concentramento nazista di Terezin.

L’internamento nel campo di Terezin

Della storia del campo di Terezin ha scritto Serena in queste pagine.
Tragica mistificazione nazista, la cittadina fortificata di Terezin, situata nel territorio che oggi è della repubblica Ceca, doveva dimostrare al mondo che gli ebrei nei campi erano tenuti in condizioni più che dignitose.
Sgombrati i 7.000 abitanti, Terezin arrivò a contenere anche 70.000 ebrei internati. Il campo era destinato a intellettuali, accademici, artisti, ai quali fu lasciata una relativa libertà di operare nel proprio campo. Le condizioni dei deportati non erano comunque molto diverse da quelle degli altri campi e la destinazione finale era la morte (molti finirono ad Auschwitz-Birkenau).

Perché i nazisti consentirono questa limitata forma di libertà a Terezin? La risposta è semplice: ad uso propaganda.
La finzione portò addirittura a un’ispezione di Terezin da parte della Croce Rossa, chiesta nel 1944 dal governo della Danimarca occupata come precondizione alla deportazione degli ebrei danesi. Andò così bene che i Nazisti pensarono di replicare con un filmato della vita nel campo, la cui regia fu affidata a Kurt Gerron, attore e regista che aveva lavorato anche con Marlene Dietrich.
Gerron, ebreo e internato a Terezin anche lui, forse pensò che questa forma di collaborazione potesse risparmiargli il viaggio finale verso Auschwitz. Ma non fu così.

Georg Pick arrivò a Terezin nel luglio del 1942, sulla soglia degli 83 anni. Resistette appena due settimane, lasciando questo mondo il 26 luglio.

Il teorema di Pick

L’enunciato del teorema fu pubblicato nel 1899, nel Geometrisches zur Zahlenlehre (Risultati geometrici della teoria dei numeri).
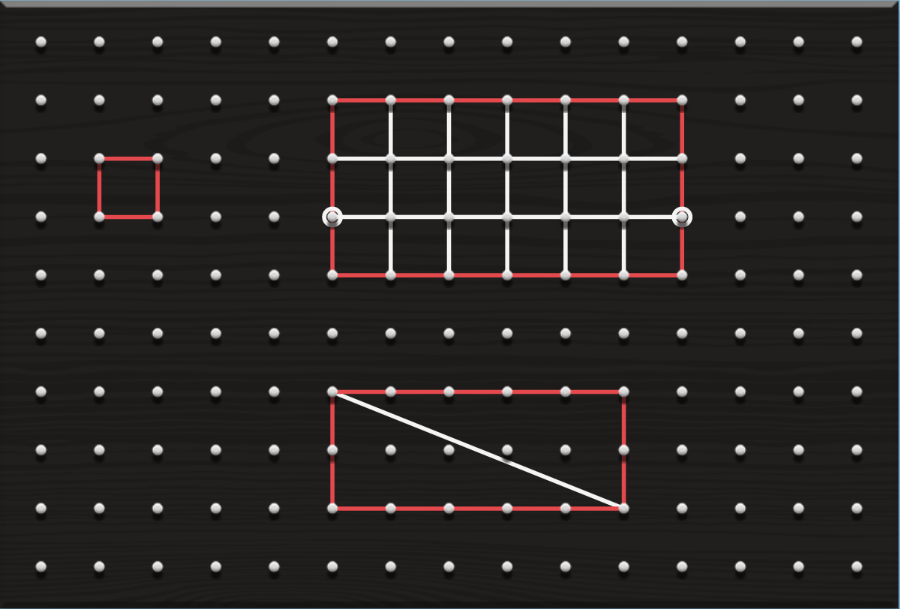
La figura di apertura di questo articolo mostra un poligono, decisamente irregolare, costruito su una geoboard.
Il teorema di Pick consente di calcolare l’area di questo poligono semplicemente contando i piolini che sono sul bordo del poligono, e quelli che sono all’interno. Detto B il numero dei primi, e I quello dei secondi, l’area del poligono è semplicemente:

A = B ⁄ 2 + I – 1

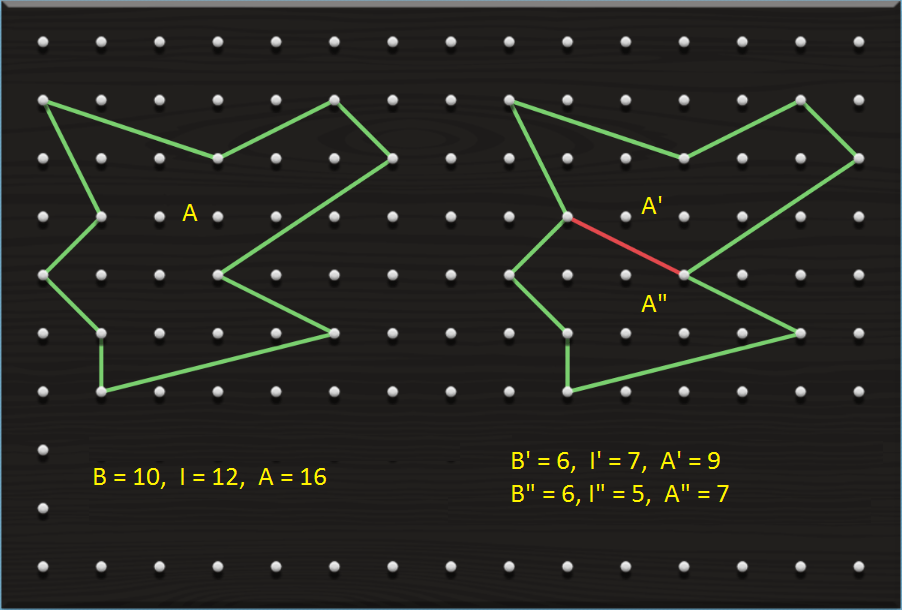
Nel caso della figura di apertura del post, per il poligono a sinistra:

B = 10,  I = 12,  quindi Area = 10 ⁄ 2 + 12 – 1 = 16

L’unica condizione è che il poligono abbia una linea chiusa semplice (senza nodi) come bordo, e non abbia buchi. Nel caso che all’interno del poligono ci siano H buchi, anch’essi contornati da una linea chiusa semplice, allora la formula del teorema di Pick si generalizza in:

A = B ⁄ 2 + I + H – 1

A prima vista sembrerebbe che l’area aumenti. Occorre però considerare che diminuisce il numero di punti interni, o perché cadono nel buco, oppure perché si trasformano da interni a bordo, e quindi pesano la metà nella formula.

Un interessante corollario del teorema di Pick

È possibile tracciare un triangolo equilatero su un reticolo regolare di punti?
Può darsi che ci si ricordi che l’area di un triangolo equilatero è data da:

A = L² √3 ⁄ 4

dove L è il lato del triangolo equilatero in questione.
Ora, l’area di un qualunque poligono costruito sul reticolo regolare di punti è espresso da un numero razionale, ci dice Pick. Ne segue che sul reticolo non può esistere nessun poligono con area espressa da un numero irrazionale (effetto del fattore √3). E quindi non può realizzarsi nemmeno il nostro triangolo equilatero.

La dimostrazione del teorema di Pick in tre semplici passi

Nel tempo sono state pubblicate diverse dimostrazioni del teorema di Pick.
Quella che segue si basa sul principio di induzione, una sorta di effetto dòmino: la validità del teorema per poche forme elementari di poligoni reticolari si propaga a catena fino alla validità per qualunque forma di poligono reticolare, assumendo, anche senza riscriverlo ogni volta, che non abbia buchi.

Il procedimento si articola quindi su tre passi:

1. procurarsi un’arma: dimostro che, dividendo un qualunque poligono reticolare in due pezzi, se il teorema vale per ciascuno dei due pezzi, allora vale anche per il poligono intero;
2. semplificare il problema: divido il poligono in pezzi elementari;
3. gran finale: dimostro che il teorema vale per tutti i pezzi elementari, quindi per induzione vale per il poligono di partenza.

Primo passo: la base per il procedimento di induzione

Se il poligono reticolare ha almeno quattro vertici, allora lo si può dividere in due pezzi, unendo tra loro due vertici non consecutivi. Siano B₁, I₁, B₂ e I₂ rispettivamente il numero dei punti reticolari sul contorno e quello dei punti interni dei due pezzi 1 e 2.
Suppongo che il teorema di Pick sia valido per entrambi i pezzi in cui ho diviso il poligono, quindi che:

A₁ = B₁  ⁄ 2 + I₁ – 1
A₂ = B₂  ⁄ 2 + I₂ – 1

L’area del poligono sarà uguale alla somma delle aree dei due pezzi, quindi:

A = A₁ + A₂  = (B₁ + B₂) ⁄2 + (I₁ + I₂) – 2,
che si può riscrivere come:
A = (B₁ + B₂ – 2) ⁄2 + (I₁ + I₂) – 1

Ora, se il taglio non contiene punti interni, allora:  I = I₁ + I₂.
I due estremi del taglio vengono contati sul contorno due volte, una per ciascun pezzo, quindi: B = B₁ + B₂ – 2.
Quindi:

A = B ⁄ 2 + I – 1

e il teorema di Pick vale in questo caso anche per il poligono intero.

Se invece il taglio contiene dei punti interni, questi diventano punti di contorno di entrambi i pezzi. Quindi vengono contati due volte ma con peso metà e il valore della formula non cambia.

Anche in questo secondo caso, quindi, il teorema di Pick vale per il poligono intero, se vale per ciascuna delle sue parti.

Ancora sulla scomposizione del poligono

Con ragionamento analogo si può concludere che, se il teorema di Pick vale per il poligono e una delle due parti in cui è diviso, allora vale anche per l’altra parte. Questa osservazione ci aiuterà tra poco.

Siano A e A₁ l’area del poligono e di una delle sue parti, e che per entrambi valga il teorema di Pick. Si ha:

A = B   ⁄2 + I – 1
A₁ = B₁  ⁄ 2 + I₁ – 1
l’area della seconda parte A₂ è pari a:
A₂  = A – A₁ = (B –  B₁ )  ⁄ 2  + (I – I₁ )
che si può scrivere anche come:
A₂  = (B –  B₁ + 2)  ⁄ 2  + (I – I₁ ) – 1

Se il lato che divide il poligono non ha punti reticolari interni al poligono, allora  I₂  = I – I₁, mentre il numero di punti reticolari di contorno B₂ si ottiene come B –  B₁, aggiungendo poi i due estremi del lato di separazione. Quindi la formula di Pick vale anche per l’area A₂.

Se, invece, il lato di divisione contiene dei punti reticolari interni al poligono, allora questi si trasformano da punti interni contati una volta sola, a punti di confine contati due volte con peso pari a metà. Quindi il valore di A₂ è anche in questo caso espresso dalla formula di Pick.

Secondo passo: dividere il poligono in pezzi elementari

Unendo opportunamente vertici non consecutivi, qualunque poligono reticolare può essere scomposto in triangoli reticolari.
Basterà quindi dimostrare che il teorema di Pick vale per ogni possibile triangolo reticolare.

Terzo passo: il teorema vale per ogni possibile triangolo reticolare (parte 1)

Prima osservazione: il teorema vale per ogni quadratino di lato 1. Infatti in questo caso si ha:

B = 4, I = 0,
quindi: A = 4 ⁄2 + 0 – 1 = 1

Ricordando quanto dimostrato nel primo passo, risulta che il teorema vale anche per qualunque rettangolo reticolare, che può essere costruito aggregando via via quadratini di lato 1.

Passiamo ora ai triangoli.
Se divido un rettangolo reticolare mediante una diagonale, ottengo due triangoli rettangoli, con i cateti paralleli alle linee del reticolo, ciascuno con area pari a metà di quella del rettangolo.

Detti B_T e I_T rispettivamente il numero di punti reticolari sul contorno e interni di ciascuno dei due triangoli, verifichiamo che effettivamente la quantità:

A_T = B_T  ⁄  2 + I_T – 1

sia uguale all’area di ciascuno dei due triangoli.

Anche qui vanno distinti due casi.

Se la diagonale non passa per nessun punto interno, allora:

B_T = B  ⁄ 2 + 1
I_T = I  ⁄ 2,
e quindi:
A_T = A  ⁄ 2 =  (B  ⁄ 2  + I – 1)  ⁄ 2 =
= (B  ⁄ 2 + 1 )  ⁄ 2 + I  ⁄ 2 – 1 =
= B_T  ⁄  2 + I_T – 1

Se la diagonale passa per alcuni punti interni, questi si trasformano in punti di contorno di entrambi i triangoli, con peso metà nella formula. Il teorema di Pick vale quindi anche in questo caso, con i valori corretti di B_T  e I_T.

La validità del teorema è dimostrata quindi per i triangoli rettangoli con i cateti paralleli alle linee del reticolo. Cosa accade a un triangolo qualunque?

Terzo passo: il teorema vale per ogni possibile triangolo reticolare (parte 2)

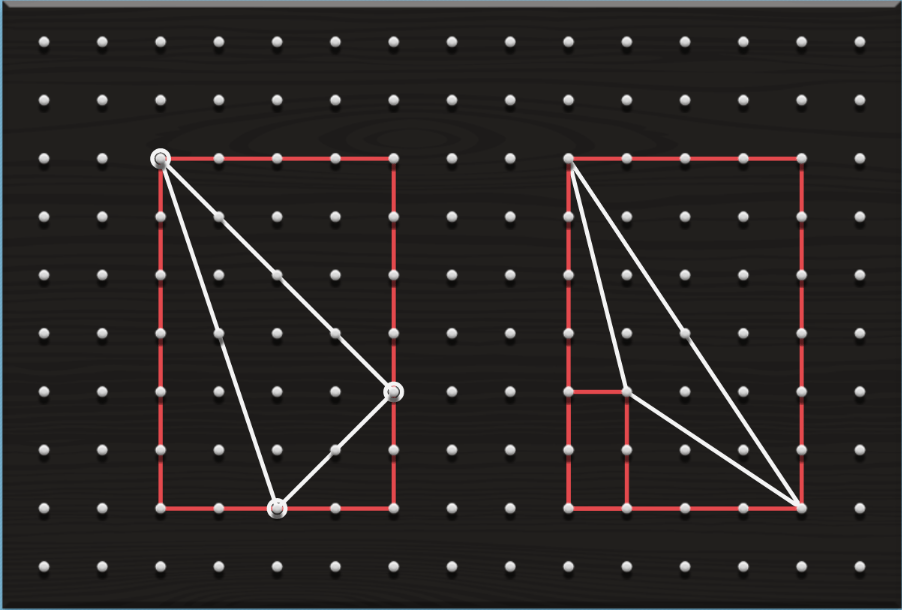
Nella figura sono riportati i due casi che possono aversi nel caso di triangolo reticolare con nessun lato parallelo alle linee del reticolo.

In entrambi i casi sappiamo che il teorema di Pick vale per i rettangoli rossi e per i triangoli rettangoli con cateti paralleli alle linee del reticolo.

Abbiamo anche visto che, partendo da un poligono e sottraendo una parte, se il teorema di Pick vale per entrambe, allora vale anche per la parte che rimane.

Quindi, partendo dal rettangolo che contorna il triangolo bianco, si possono via via sottrarre le altre parti, fino a lasciare il triangolo bianco.

A questo punto il teorema è dimostrato (salvo sviste).

---

L’aspetto che più colpisce in casi come questi è il lampo di genio che ha consentito di cogliere l’esistenza di un legame di stretta dipendenza tra due entità apparentemente distinte, come l’area del poligono e il conteggio dei suoi punti interni e di contorno.
Questo legame ha infatti una conseguenza controintuitiva: l’area di un poligono reticolare è espressa sempre da un numero intero o al massimo metà di un intero. Qualunque sia l’inclinazione, il numero e la lunghezza dei lati.

Assolutamente affascinante.