Algoritmo di accelerazione della somma di una serie

Come promesso nell’articolo precedente, ecco il mio algoritmo di accelerazione della somma di serie numeriche.
Non è certamente un campione di efficienza, ma ha il pregio di poter essere applicato a serie diverse e implementato con poche linee di codice.

Il problema di partenza

Nell’articolo precedente si è visto che c’è un’area ancora da esplorare nel problema di Basilea: la determinazione di una forma chiusa per le somme delle potenze dispari dei numeri naturali.
Se, infatti, Eulero ha dimostrato che:

∑ 1 ⁄ n² = π²⁄ 6, ∑ 1 ⁄ n⁴ = π⁴ ⁄ 90,

e così via fino alla 26ma potenza pari, risultato poi esteso a tutte le potenze pari, la questione rimane tuttora aperta per le potenze dispari, a partire da ∑ 1⁄n³, somma detta anche costante di Apéry.
Nel seguito si indicheranno queste somme con il simbolo ζ(2), ζ(3), …, poiché rappresentano particolari valori della funzione zeta di Riemann, definita come:

ζ(s) = ∑ 1⁄n^s

Perché serve un algoritmo di accelerazione

Uno dei primi passi che viene in mente di fare è quello di calcolare un po’ di cifre di queste somme, per provare a trovare visivamente ricorrenze, sia nelle somme stesse che nei loro rapporti.
Se, ad esempio, valesse anche per le potenze dispari una relazione di proporzionalità con le potenze di π, allora ζ(5) ⁄ ζ(3) dovrebbe essere proporzionale a π².

Per calcolare un po’ di cifre di ζ(3), la costante di Apéry, bastano in effetti poche righe di codice in un linguaggio come Ubasic o Ruby. Naturalmente più termini della serie vengono sommati, più ci si avvicina al valore di ζ(3) = 1,202056903159594…
Questo approccio diretto presenta due inconvenienti.
Il primo: i termini decrescono molto lentamente. Il 50mo termine, ad esempio, è pari a 0,000008, il successivo a 0,0000075… Quindi ci si avvicina a piccolissimi passi al risultato voluto.
L’altro inconveniente è che non si ha una stima dell’errore che si commette fermandosi dopo, ad esempio, 50 termini.

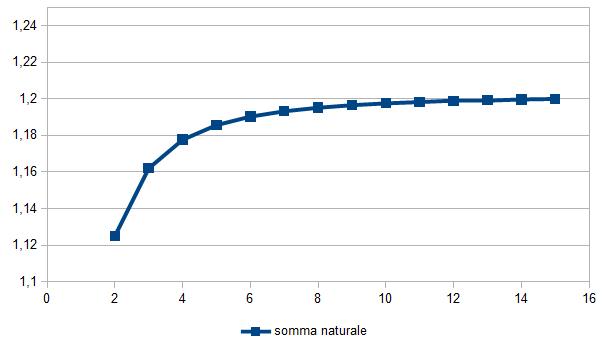
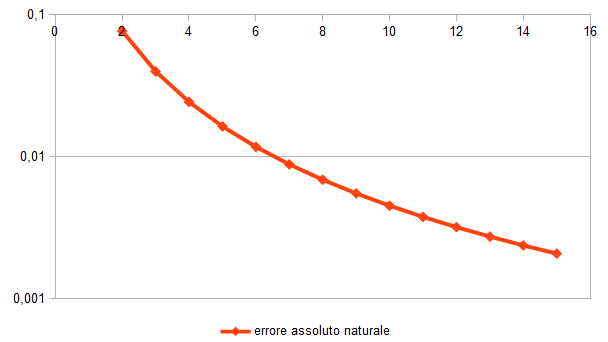
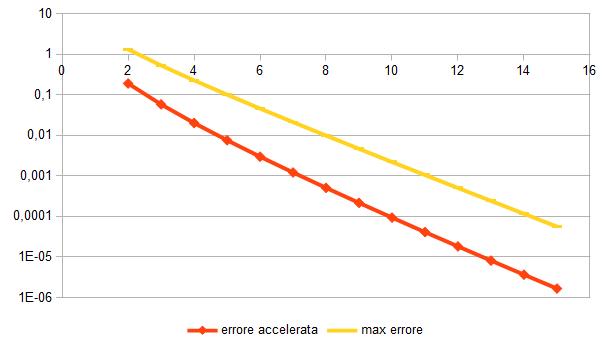
Le figure riportate qui di seguito mostrano l’andamento della somma e dell’errore ottenuti con questo metodo, che ho indicato come naturale, in funzione del numero di termini considerati.

Un primo algoritmo di accelerazione: trasformare in somma a termini alterni

Un modo per superare questi due inconvenienti è quello di trasformare la somma in un’altra che dia lo stesso risultato ma che abbia termini con segno alternato. Si dimostra infatti che questo tipo di somma converge più rapidamente ma, soprattutto, consente una stima dell’errore commesso fermando il calcolo dopo un certo numero di passi. In particolare l’errore sarà minore del primo termine trascurato; errore in eccesso se questo termine è negativo, errore in difetto se è positivo.

Trasformare la nostra serie è molto semplice. La somma della serie a termini alterni:

∑ (-1)^n-1 ⁄ n³

è intuitivamente uguale alla somma dei termini con n dispari, meno quella dei termini con n pari. Ora:

∑ 1 ⁄ (2n)³ = ∑ 1 ⁄ 8 n³ = 1 ⁄ 8 ∑ 1 ⁄ n³ = 1 ⁄ 8 ζ(3).

Se la somma dei termini pari è 1 ⁄ 8 della somma completa, allora il rimanente, cioè i 7 ⁄ 8, sarà la somma dei termini dispari. Quindi:

∑ (-1)^n-1 ⁄ n³ = 7 ⁄ 8 ζ(3) – 1 ⁄ 8 ζ(3) = 3 ⁄ 4 ζ(3), e quindi:
ζ(3) = 4 ⁄ 3 ∑ (-1)^n-1 ⁄ n³

Cosa si guadagna con questa trasformazione?

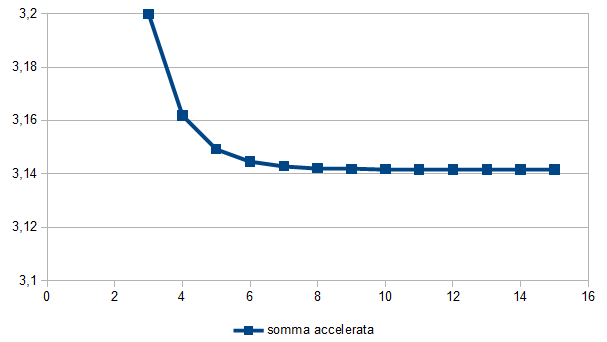
Le figure che seguono ci danno una vista del miglioramento ottenuto.

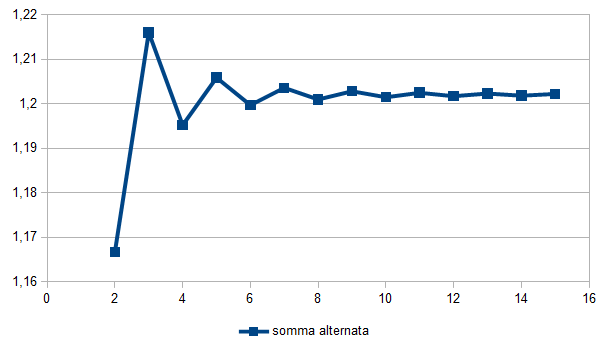
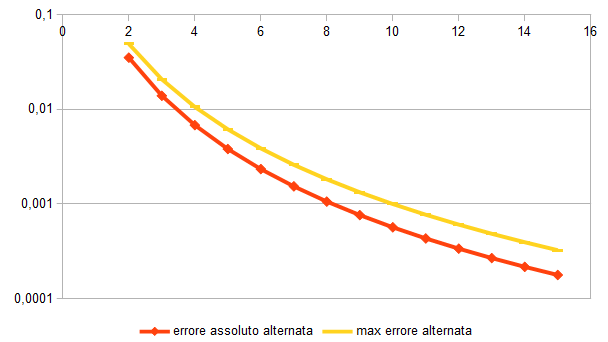
Innanzitutto si vede l’andamento alternato del valore ottenuto fermandosi dopo 2, 3, … 15 termini. Nella seconda figura si apprezza invece che l’errore è diminuito, si passa da 2 a 3 cifre corrette sommando i primi 15 termini della serie. Inoltre è evidente il maggior controllo sull’errore: adesso abbiamo una stima per eccesso, che non si discosta molto dall’errore effettivo.

Rimane però una certa lentezza nel convergere. Nella seconda figura sarebbe bello poter avere linee che vadano giù dritte, aggiungendo una nuova cifra esatta dopo un numero costante di termini.

L’algoritmo di accelerazione

Si ragioni ora su una generica serie a termini alterni:

S = ∑ (-1)^n-1 a_n = a₁ – a₂ + a₃ – a₄ + …

È possibile riscrivere la somma in due modi differenti, accorpando i termini a due a due:

S = (a₁ – a₂) + (a₃ – a₄) + …

S = a₁ – (a₂ – a₃) – (a₄ – a₅) – …

Sommando le due espressioni si ha:

2S = (2a₁ – a₂) – (a₂ – a₃) + (a₃ – a₄) – (a₄ – a₅)+ …

Si ottiene quindi ancora una serie a termini alterni, in cui il primo termine è (2a₁ – a₂)/2, il secondo (a₂ – a₃)/2.

Dal punto di vista computazionale, approssimare il valore della somma calcolando solo il primo termine equivale ad approssimare la somma originaria calcolando i primi due termini.
Cosa succederebbe all’errore in questi due casi?
Nel primo caso l’errore è minore di (a₂ – a₃) ⁄ 2, nel secondo minore di a₃. Quindi, se (a₂ – a₃) ⁄ 2 < a₃, cioè se a₂ < 3a₃, allora si ottiene effettivamente un’accelerazione della convergenza.

Nel caso della costante di Apéry:

a₂ = 1 ⁄ 8
a₃ = 1 / 27

quindi non si è ottenuto un miglioramento, anzi l’errore è aumentato.

Proviamo a insistere

Si riapplichi il ragionamento alla nuova serie alternata che è stata determinata, più e più volte.
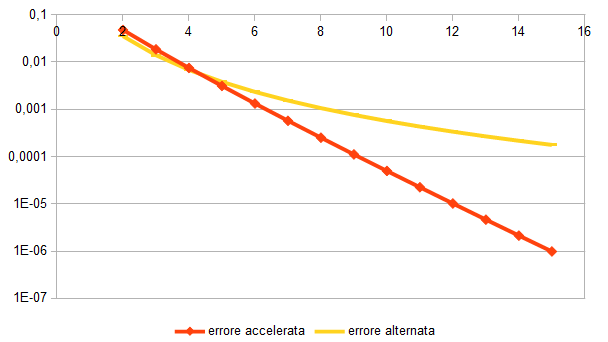
Il grafico che segue riporta l’andamento dell’errore di entrambe le serie: per quella accelerata fermandosi al primo termine, per quella alternata originaria fermandosi al numero di termini computazionalmente equivalente:

Si vede che già con 5 termini la serie accelerata presenta un errore minore dell’altra. Ma, cosa ancora più importante, la linea dell’errore va giù dritta, apportando al risultato una nuova cifra corretta ogni 3 termini circa.

L’algoritmo di accelerazione funziona anche con altre serie?

Ho provato l’algoritmo su altre serie alternate che presentano una convergenza molto lenta. Ad esempio a:

π = 4 ∑ (-1)^n-1 ⁄ (2n – 1)

Le figure che seguono mostrano la convergenza e l’andamento dell’errore:

Si notano due cose:

l’approssimazione avviene sempre per eccesso, perché il primo termine trascurato (il secondo della serie accelerata) è sempre negativo;
anche in questo caso si ottiene una nuova cifra corretta ogni tre termini circa.

Il codice per l’algoritmo di accelerazione

Chi volesse divertirsi a giocare con questo algoritmo, trova qui un semplice programma Ruby, impostato per calcolare l’approssimazione della costante di Apery, oltre che quella della serie che somma a π e infine di una serie alternata che somma al logaritmo naturale di 2.
Da notare che il programma non produce direttamente i grafici, bensì dati in formato csv che, inseriti in un file excel (scaricabile con lo zip precedente), consentono di produrre rapidamente i grafici. Utilizzo questo approccio sostanzialmente perché sono pigro.

Ecco l’output del programma, per il calcolo della costante di Apéry:

n.ro termini:   somma:          errore:         max errore:
          2     1.250000000000  0.04794310      0.05864198
          3     1.220679012346  0.01862211      0.02218364
          4     1.209587191358  0.00753029      0.00879398
          5     1.205190200617  0.00313330      0.00360262
          6     1.203388888889  0.00133199      0.00151240
          7     1.202632690742  0.00057579      0.00064703
          8     1.202309173702  0.00025227      0.00028103
          9     1.202168661093  0.00011176      0.00012357
         10     1.202106874544  0.00004997      0.00005490
         11     1.202079424635  0.00002252      0.00002460
         12     1.202067122729  0.00001022      0.00001111
         13     1.202061568137  0.00000466      0.00000505
         14     1.202059043773  0.00000214      0.00000231
         15     1.202057889990  0.00000099      0.00000106

pesi della somma: [16384, -16383, 16369, -16278, 15914, -14913, 12911,
                  -9908, 6476, -3473, 1471, -470, 106, -15, 1]
pesi della stima dell'errore: [1, -14, 91, -364, 1001, -2002, 3003,
                  -3432, 3003, -2002, 1001, -364, 91, -14, 1]

Da qualche parte dovrei avere anche il programma, scritto in Ubasic, che calcola le prime 1.000 cifre della costante di Apéry (e di π ). Perché Ubasic? Ancora una volta per pigrizia: Ubasic consente di utilizzare variabili con 1.000 cifre significative e oltre, quindi ci si risparmia di realizzare da programma la precisione di calcolo richiesta.
Appena ritrovo il programma lo rendo scaricabile da questo articolo. Promesso.