42, la risposta alla domanda fondamentale sulla vita

A distanza di 65 anni dal lancio della sfida da parte dell’Università di Cambridge, è andato a posto anche il 42, ultimo dei tasselli della soluzione dell’equazione di Mordell:

x³ + y³ + z³ = k
per valori interi di x, y e z, e con k compreso tra 1 e 100.

Negli anni dal 1954 ad oggi, infatti, è stata trovata una risposta per tutti i valori di k. L’ultimo a cadere è stato il valore 42, lo scorso 6 settembre, quando i professori Andrew Booker dell’Università di Bristol e Andrew Sutherland del Massachusetts Institute of Technology (MIT) hanno annunciato che:

-80538738812075974³ + 80435758145817515³ + 12602123297335631³ = 42

Un numero importante, il 42. Chi ha letto la Guida intergalattica per autostoppisti ricorderà infatti che la risposta alla domanda fondamentale sulla vita, l’universo e tutto quanto, fornita dal supercomputer Pensiero Profondo, è proprio 42.
Dal libro nel 2005 fu pure tratto un film, Non ha fatto grandi numeri, in Italia è rimasto in visione per una sola settimana, ma ha visto la partecipazione, di John Malkovich e Helen Mirren (la voce di Pensiero Profondo). Il film è disponibile su Netflix e in frammenti su Youtube.

Cos’è l’equazione di Mordell e perché è così complicato risolverla?

---

La definizione del problema

Si richiede di trovare tre numeri interi, x, y e z, la somma dei cui cubi sia un numero intero positivo k, compreso tra 1 e 100. Successivamente il problema è stato esteso ai valori di k compresi tra 1 e 1.000.
Attualmente, risolti tutti i casi con k compreso tra 1 e 100, rimangono senza risposta solo 9 dei 1.000 casi possibili, il più piccolo dei quali è k = 114.
È stato ipotizzato che, se per un determinato k esiste una soluzione per x,y,z, allora ne esistono infinite.

Un super computer per un super calcolo

La terna x,y,z che risolve il caso k = 42 è stata trovata grazie ad alcune settimane di calcolo sulla rete di Charityengine.com.
La rete è composta da più di 1.000.000 di pc sparsi in oltre 300 Paesi e ne sfrutta i tempi di inattività. La sua capacità di calcolo può essere affittata per progetti che richiedono, come nel caso delle soluzioni dell’equazione di Mordell, un processing intensivo.
I vantaggi? È una risorsa ecologica (si tratta di pc che esistono e vengono, generalmente, lasciati accesi). Costa molto meno dell’affitto di server virtuali su Amazon o Microsoft Azure e, inoltre, metà dei profitti vengono devoluti in azioni benefiche.

Lo stesso programma ha risposto, qualche giorno dopo, il 18 settembre, anche a un’altra questione in attesa da molti anni:

esiste una soluzione per il caso k = 3, oltre alle due soluzioni molto semplici:
1³ + 1³ + 1³ = 3, e
4³ + 4³ + (-5)³ = 3 ?

Una terza terna esiste ed è:
569936821221962380720³ + (-569936821113563493509)³ + (-472715493453327032)³ = 3.

Di passaggio, il programma ha anche risolto il caso k = 906. Trovare la terza soluzione del caso k = 3 ha richiesto 4.000.000 di ore di calcolo, equivalenti  a 456 anni.

Come si affronta un problema del genere

Il primo elaboratore a cui ricorrere è ovviamente il cervello: si può arrivare alla soluzione mediante deduzioni logiche? Nel nostro caso l’aritmetica modulare, già incontrata in questo articolo, ci fornisce le prime importanti risposte.

Ciascuna delle incognite x, y e z, infatti, quando divisa per 3, potrà dare resto 0, 1, oppure 2. Questo valore viene definito il valore modulo 3 del numero di partenza: x modulo 3 = 0, 1 oppure 2. Si osservi anche che 2 modulo 3 = -1.
Analogamente, i valori possibili di un numero modulo 9 sono ovviamente: 0, 1, 2, …, 8, che possono essere anche scritti come -4, -3, -2, -1, 0, 1, 2, 3, 4.

Ora, si scriva ciascuna incognita evidenziandone il valore modulo 3. Es.: x = 3k + r, dove r = 0, 1 oppure -1.
Quindi:

x³ = (3k + r)³ = 27k³ + 27k²r + 9kr²  + r³

I primi tre termini sono multipli di 9, quindi sono equivalenti a 0, modulo 9. Se ne deduce quindi che:

x³ modulo 9 = r³ = 0, 1 oppure -1

Lo stesso discorso vale per y³ e z³, per cui la somma dei cubi delle tre incognite potrà assumere i valori: -3, -2, -1, 0, 1, 2 oppure 3, ma non -4 oppure 4.

In base a questo semplice ragionamento si può dedurre quindi che l’equazione non potrà avere soluzioni per valori di k che abbiano -4 oppure 4 come valori modulo 9.

Nell’arco da 1 a 100 questo ci risolve, seppure in modo negativo, i casi di k pari a:

4, 5, 13, 14, 22, 23, 31, 32, 40, 41, 49, 50, 58, 59, 67, 68, 76, 77, 85, 86, 94, 95.

Dei 100 possibili valori di k, quindi, i primi 22 hanno trovato una risposta: nessuna terna x, y, z risolve l’equazione. Rimangono da risolvere 100 – 22 = 78 casi.

Prima o poi si deve ricorrere al computer

Per i restanti casi si può procedere esplorando le possibili terne e calcolandone il valore. Un possibile frammento di codice in Ruby è questo:

(1..xmax).each do |x|
	(x..ymax).each do |y|
		(y..zmax).each do |z|
			n = x**3 + y**3 + z**3
			break if n > 1000
			if n > 100 then
				lista1k.write("#{n},#{x},#{y},#{z}\n")
			else
				lista100.write("#{n},#{x},#{y},#{z}\n")
			end
		end
	end
end

Il programma esplora x, y e z da 1 fino a valori massimi fissati e, se la somme dei cubi è non maggiore di 100, o di 1000, annota la terna in un apposito file.
Con questo metodo vengono risolti pochi casi. Per k tra 1 e 100, ad esempio, si trova una soluzione per altri 15 valori di k:

3, 10, 17, 24, 29, 36, 43, 55, 62, 66, 73, 80, 81, 92, 99.

Per  trovare altre soluzioni occorre cercare terne in cui uno o due termini siano negativi, come nel caso delle soluzioni trovate dal programma dei professori Booker e Sutherland. Per farlo occorre un programma più articolato, che è possibile scaricare da qui, nella cartella compressa contenente i programmi preparati per questo articolo con i relativi dati.
Con il programma esteso, esplorando le terne per valori di x, y e z non superiori a 5.000, gli unici valori di k ancora in attesa di soluzione rimangono questi 8:

30, 33, 39, 42, 52, 74, 75, 84.

Il caso per k = 33 è stato il penultimo ad essere risolto, appena prima del caso “42”, sempre dal professor Booker, lo scorso febbraio.

Un esempio di soluzione trovata dal nostro programma in Ruby:

3753³ + 4528³ + (-5262)³ = 1

Come si affrontano i casi più complessi?

Per spingersi oltre occorre sia grande potenza di calcolo che algoritmi per restringere l’analisi a un numero ristretto di possibili candidati e per parallelizzare le operazioni, riducendo il tempo di attesa dell’esito del calcolo.
L’algoritmo dei professori Booker e Sutherland è estremamente efficiente, ma complesso nei suoi dettagli. Un algoritmo molto elementare si può utilizzare, invece, per il caso k = 39, risolto negli anni ’60. Anche in questo caso ricorriamo all’aritmetica modulare.

Osserviamo infatti che 39 modulo 9 = 3 (39 diviso 9 dà resto 3). Ricordando che il valore modulo 9 dei tre cubi può essere -1, 0 oppure 1, si deduce che l’unico valore possibile per ciascuno di essi è 1 (1 + 1 + 1 = 3).

In precedenza si è anche visto che per ognuna delle incognite vale la relazione:

se x modulo 3 = r
allora x³ modulo 9 = r³

Poiché r³ = 1, allora r = 1.
Questa osservazione consente di eliminare due casi su tre, riducendo il tempo di elaborazione a 1/3. Un breve programma in Ruby ha consentito, dopo 1^h07’33” di elaborazione sul mio pc, di trovare la soluzione:

117367³ + 134476³ + (-159380)³ = 39.

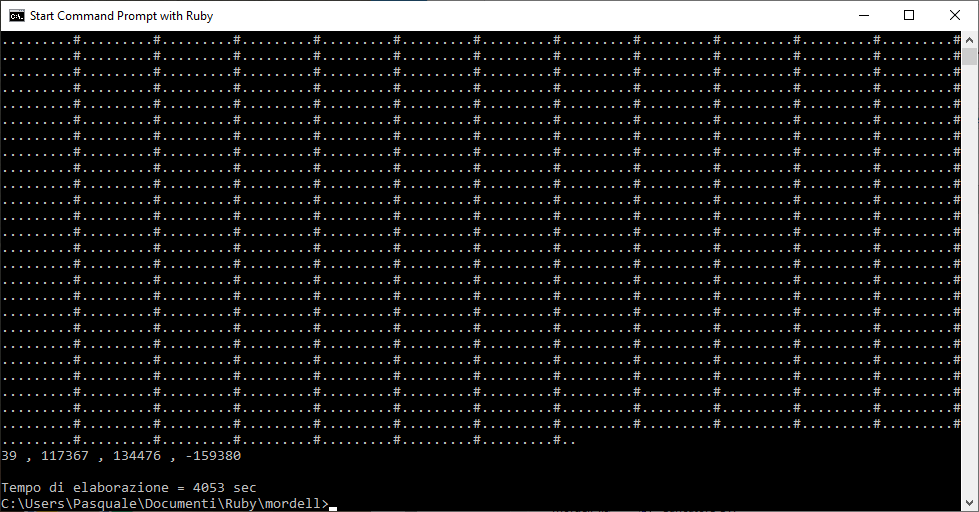
Per avere una sensazione visiva dello stato di esecuzione del programma, viene stampato a video un carattere “#” ogni 100 passi di esecuzione del programma e il carattere “.” ogni 10.
Inoltre è stato necessario disabilitare, nelle impostazioni di Windows 10, il passaggio del pc allo stato di stand-by dopo un certo periodo di non attività da tastiera/trackpad.

Calcolo parallelo, anche sul pc

Il mio PC ha un processore con 2 core e 4 thread. Tradotto in linguaggio comprensibile, il processore è capace di gestire contemporaneamente 4 flussi di esecuzione, assegnati a 2 processori fisici.
L’interprete Ruby utilizza un solo flusso di esecuzione, per cui, anche se il PC ha come unica applicazione in esecuzione il programma Ruby, questo non potrà utilizzare più del 25% della capacità di calcolo disponibile.

Si può aumentare la percentuale di utilizzo del PC, da parte del nostro algoritmo? Per farlo occorre trovare un modo per eseguire più calcoli in parallelo.

Si è visto che la soluzione cercata può essere di uno di due possibili tipi:

negativo³ + negativo³ + positivo³ = k
positivo³ + positivo³ + negativo³ = k

E il programma, in effetti, ad ogni iterazione, verifica in serie l’esistenza prima di una soluzione del primo tipo, poi di una del secondo. È quindi possibile spezzare il programma in due programmi distinti, uno che cerca soluzioni del primo tipo, l’altro soluzioni del secondo tipo, e poi eseguire contemporaneamente i due programmi.

Ecco i risultati dei due programmi:

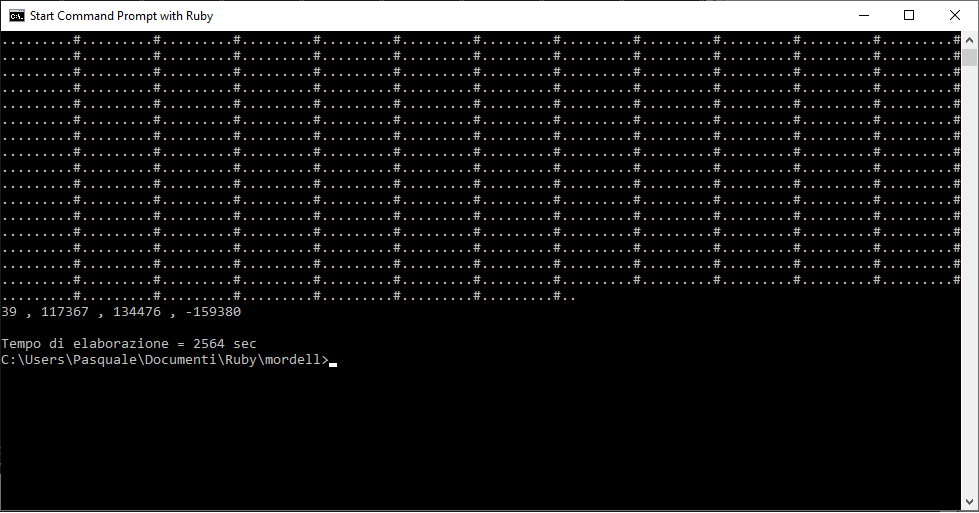
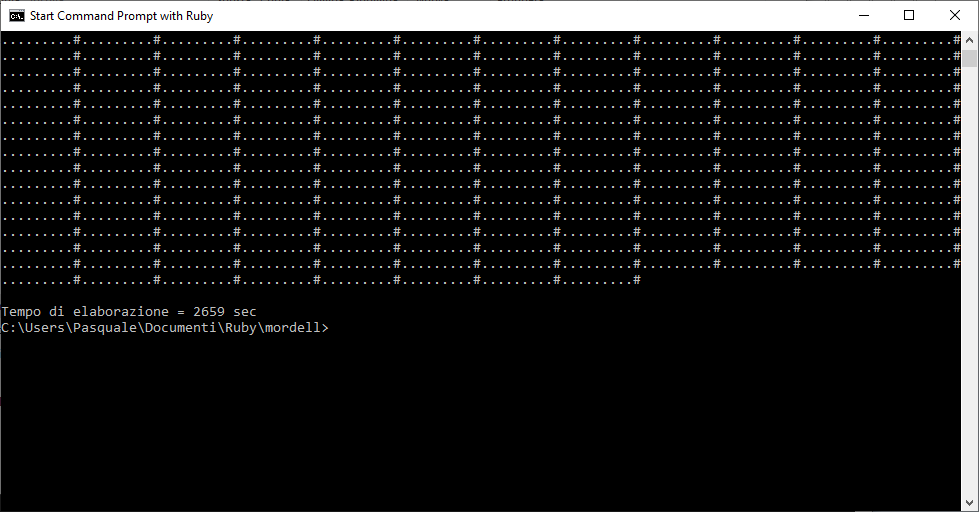
Come si vede la soluzione viene trovata in 2564 secondi, equivalenti a 42’44”. L’altra metà del calcolo termina in 2659 secondi, cioè dopo 44’19”. Non si è ottenuto proprio un dimezzamento del tempo di attesa, ma il miglioramento è comunque notevole.
Anche questi due programmi si trovano nell’archivio compresso scaricabile da qui.

Ancora un’altra parallelizzazione possibile

Visto che il PC ha 4 thread di esecuzione, si potrebbe spezzare in due ciascuno dei due programmi, ottenendo così 4 porzioni di algoritmo da eseguire simultaneamente.

Un modo molto semplice per farlo consiste nel dividere il campo di valori dell’incognita che viene esplorato (j da 10 a 50.000) in due campi parziali: j da 10 a 15.000 e j da 15.001 a 50.000. LA suddivisione è fatta a occhio, tenendo conto del fatto che l’arco di calcolo si riduce al crescere di j.
Non ho realizzato la prova, non ne valeva la pena. Il tempo di preparazione dei programmi non sarebbe stato ricompensato dalla riduzione del tempo di attesa a mezz’ora o poco più.

---

La guida intergalattica per autostoppisti

Chissà quale entità sovrannaturale guidò lo scrittore inglese Douglas Adams a scegliere proprio 42 come “risposta alla domanda fondamentale sulla vita, l’universo e tutto quanto“, nella sua “Guida intergalattica per autostoppisti”.
La famosa “trilogia in cinque parti” uscì nel 1979 ed è la trasposizione in testo, per nulla fedele, delle puntate di una serie radiofonica ideata per la BBC dallo stesso Douglas Adams. La trilogia arrivò in Italia a partire dall’anno successivo, nella collana di fantascienza Urania.

A fornire la risposta “42” è Deep Thought, Pensiero profondo, il “secondo più grande computer dell’Universo del Tempo e dello Spazio“. 

“Quarantadue!” urlò Loonquawl. “Questo è tutto ciò che sai dire dopo un lavoro di sette milioni e mezzo di anni?”
“Ho controllato molto approfonditamente,” disse il computer, “e questa è sicuramente la risposta. Ad essere sinceri, penso che il problema sia che voi non abbiate mai saputo veramente qual è la domanda.”

Il primo più grande computer dell’Universo ecc. ecc. è invece il pianeta Terra! Popolato da individui simili a scimmie, il pianeta viene demolito dagli alieni Vogon per far posto ad una nuova superstrada iperspaziale.
Lo scopo della Terra è di fornire la Domanda alla Risposta. Purtroppo la demolizione avviene dopo 10 milioni di anni di calcolo, appena 5 minuti prima che l’elaborazione abbia termine.
La serie di super-elaboratori IBM a cui appartiene Deep Blue, il primo elaboratore a sconfiggere un campione del mondo di scacchi (Garry Kasparov), cominciò con un Deep Thought, ispirato proprio alla Guida intergalattica di Douglas Adams.

Foto di apertura di Benjamin Balazs da Pixabay.